Dynamic Portfolio Management with Multi-Armed Bandits

Using Ray RLlib to enable dynamic asset allocation for a portfolio

Investment Industry
Reinforcement Learning
Multi-Armed Bandits
Ray RLlib
OpenAI Gym
Author

Kobus Esterhuysen

Published

December 7, 2021

1. BUSINESS UNDERSTANDING

Asset allocation refers to the partitioning of available funds in a portfolio among various investment products. Investment products may be categorized in multiple ways. One common (and high level) classification contains three classes:

  • Stocks
  • Bonds (fixed income)
  • Cash and cash equivalents

Other classification systems may sub-classify each of these categories into subclasses, for example stocks into US and International stocks, or into small-cap, medium-cap, and large-cap stocks, etc.

Another aspect of asset allocation is concerns the underlying strategy. Some strategies are:

  • Tactical asset allocation
  • Strategic asset allocation
  • Constant weight asset allocation
  • Integrated asset allocation
  • Insured asset allocation
  • Dynamic asset allocation

We will focus on the last of these strategies: Dynamic asset allocation. With this approach the combination of assets are adjusted at regular intervals to capitalize on the strengthening and weakening of the economy and rise and fall of markets. This strategy depends on the decisions of a portfolio manager. In this project, however, we will attempt to replace the portfolio manager with an AI agent. The agent will be trained on past market behavior by means of Multi-Armed Bandits. This is a technique encountered in the reinforcement learning paradigm.

Instead of adjusting the composition of the portfolio at regular intervals, we will take an all-or-nothing approach. This means a single asset will be selected at each interval. All the funds will be invested in the selected asset. We will revisit this selection on a monthly basis. The reason we impose this constraint on the management of the portfolio is to evaluate the usefulness of the multi-armed bandit technique. This algorithm mandates that only a single “lever” can be activated at each decision point.

For this Proof-Of-Concept (POC) project we will make things as simple as possible. The portfolio will consist of 5 mutual funds. For simplicity, trading costs will not be taken into account for now.

The following funds are used for the portfolio:

  • Fidelity® Blue Chip Value Fund (FBCVX)
  • Fidelity® Small-Cap Growth Fund (FCPGX)
  • Fidelity® Growth Discovery Fund (FDSVX)
  • Vanguard Intermediate Term Bond Index Fund - Admiral Class (VBILX)
  • S&P500 (^GSPC)

To implement this POC we will make use of the Ray RLlib framework as well as some Yahoo technology to acquire financial data. The portfolio data will come from Yahoo. We will also make use of inflation as well as Producer Price Index (PPI) data. Both the inflation and PPI data was obtained from https://fred.stlouisfed.org/

2. DATA UNDERSTANDING

Let us now obtain the data we need. We do some setting up first:

# hide
from google.colab import drive
drive.mount('/content/gdrive', force_remount=True)
root_dir = "/content/gdrive/My Drive/"
base_dir = root_dir + 'RLlib/'
# base_dir = ""
Mounted at /content/gdrive
!pip install yfinance==0.1.67
import yfinance as yf
yf.__version__
Requirement already satisfied: yfinance==0.1.67 in /usr/local/lib/python3.7/dist-packages (0.1.67)
Requirement already satisfied: pandas>=0.24 in /usr/local/lib/python3.7/dist-packages (from yfinance==0.1.67) (1.1.5)
Requirement already satisfied: numpy>=1.15 in /usr/local/lib/python3.7/dist-packages (from yfinance==0.1.67) (1.19.5)
Requirement already satisfied: requests>=2.20 in /usr/local/lib/python3.7/dist-packages (from yfinance==0.1.67) (2.23.0)
Requirement already satisfied: lxml>=4.5.1 in /usr/local/lib/python3.7/dist-packages (from yfinance==0.1.67) (4.6.4)
Requirement already satisfied: multitasking>=0.0.7 in /usr/local/lib/python3.7/dist-packages (from yfinance==0.1.67) (0.0.10)
Requirement already satisfied: pytz>=2017.2 in /usr/local/lib/python3.7/dist-packages (from pandas>=0.24->yfinance==0.1.67) (2018.9)
Requirement already satisfied: python-dateutil>=2.7.3 in /usr/local/lib/python3.7/dist-packages (from pandas>=0.24->yfinance==0.1.67) (2.8.2)
Requirement already satisfied: six>=1.5 in /usr/local/lib/python3.7/dist-packages (from python-dateutil>=2.7.3->pandas>=0.24->yfinance==0.1.67) (1.15.0)
Requirement already satisfied: urllib3!=1.25.0,!=1.25.1,<1.26,>=1.21.1 in /usr/local/lib/python3.7/dist-packages (from requests>=2.20->yfinance==0.1.67) (1.24.3)
Requirement already satisfied: chardet<4,>=3.0.2 in /usr/local/lib/python3.7/dist-packages (from requests>=2.20->yfinance==0.1.67) (3.0.4)
Requirement already satisfied: certifi>=2017.4.17 in /usr/local/lib/python3.7/dist-packages (from requests>=2.20->yfinance==0.1.67) (2021.10.8)
Requirement already satisfied: idna<3,>=2.5 in /usr/local/lib/python3.7/dist-packages (from requests>=2.20->yfinance==0.1.67) (2.10)
'0.1.67'
!pip install pandas==1.1.5
import pandas as pd
pd.__version__
Requirement already satisfied: pandas==1.1.5 in /usr/local/lib/python3.7/dist-packages (1.1.5)
Requirement already satisfied: numpy>=1.15.4 in /usr/local/lib/python3.7/dist-packages (from pandas==1.1.5) (1.19.5)
Requirement already satisfied: pytz>=2017.2 in /usr/local/lib/python3.7/dist-packages (from pandas==1.1.5) (2018.9)
Requirement already satisfied: python-dateutil>=2.7.3 in /usr/local/lib/python3.7/dist-packages (from pandas==1.1.5) (2.8.2)
Requirement already satisfied: six>=1.5 in /usr/local/lib/python3.7/dist-packages (from python-dateutil>=2.7.3->pandas==1.1.5) (1.15.0)
'1.1.5'
%matplotlib inline
from matplotlib import pyplot as plt
# import numpy as np
# import os
# import sys

The portfolio data was acquired from Yahoo finance:

df_port = yf.download(tickers="^GSPC VBILX FBCVX FDSVX FCPGX", start='2004-12-01', end='2021-11-01', interval='1mo')
df_port
[*********************100%***********************]  5 of 5 completed
Adj Close Close High Low Open Volume
FBCVX FCPGX FDSVX VBILX ^GSPC FBCVX FCPGX FDSVX VBILX ^GSPC FBCVX FCPGX FDSVX VBILX ^GSPC FBCVX FCPGX FDSVX VBILX ^GSPC FBCVX FCPGX FDSVX VBILX ^GSPC FBCVX FCPGX FDSVX VBILX ^GSPC
Date
2004-12-01 8.920976 4.448220 7.593656 5.474646 1211.920044 12.550000 11.410000 11.300000 10.68 1211.920044 12.570000 11.430000 11.310000 10.80 1217.329956 12.14 10.860000 11.060000 10.60 1173.780029 12.360000 11.050000 11.130000 10.61 1173.780029 0.0 0.0 0.0 0.0 3.110250e+10
2004-12-10 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
2004-12-17 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
2004-12-31 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
2005-01-01 8.871915 4.491105 7.228118 5.524208 1181.270020 12.420000 11.520000 10.670000 10.70 1181.270020 12.470000 11.520000 11.220000 10.71 1217.800049 12.18 10.900000 10.580000 10.63 1163.750000 12.430000 11.220000 11.220000 10.68 1211.920044 0.0 0.0 0.0 0.0 3.149880e+10
... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...
2021-09-01 22.528105 28.668407 53.279999 12.092872 4307.540039 22.680000 32.849998 53.279999 12.13 4307.540039 23.889999 40.160000 57.270000 12.31 4545.850098 22.65 32.849998 53.279999 12.11 4305.910156 23.690001 39.630001 57.009998 12.29 4528.799805 0.0 0.0 0.0 0.0 6.626885e+10
2021-09-03 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
2021-09-10 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
2021-10-01 23.780001 34.669998 57.630001 12.011015 4605.379883 23.780001 34.669998 57.630001 12.03 4605.379883 23.910000 34.669998 57.630001 12.17 4608.080078 22.75 32.560001 52.630001 11.98 4278.939941 22.820000 33.259998 53.919998 12.17 4317.160156 0.0 0.0 0.0 0.0 6.187470e+10
2021-10-29 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN

482 rows × 30 columns

The portfolio data set consists of monthly entries which have the ‘Adj Close’, ‘Close’, ‘High’, ‘Low’, ‘Open’, and ‘Volume’ for each ticker. There are many rows with ’NaN’s. The data span the time from 2004-12-01 to 2021-11-01.

Next we will get data for inflation. This was manually downloaded from https://fred.stlouisfed.org/ and stored in a file called MAB-inflation.csv.

# https://fred.stlouisfed.org/tags/series?t=inflation%3Bmonthly&ob=pv&od=desc
df_inf = pd.read_csv(base_dir+'MAB-inflation.csv')
df_inf
DATE T10YIEM
0 2004-12-01 2.56
1 2005-01-01 2.50
2 2005-02-01 2.54
3 2005-03-01 2.71
4 2005-04-01 2.63
... ... ...
199 2021-07-01 2.33
200 2021-08-01 2.35
201 2021-09-01 2.34
202 2021-10-01 2.53
203 2021-11-01 2.62

204 rows × 2 columns

This data set has an inflation entry for each month of the the same period we use for the portfolio data.

Finally, we get the data for the Producer Price Index (PPI) by downloading it manually from the same site and storing it in a file called MAB-ppi.csv.

# https://fred.stlouisfed.org/series/PPIACO
df_ppi = pd.read_csv(base_dir+'MAB-ppi.csv')
df_ppi
DATE PPIACO
0 2004-12-01 150.2
1 2005-01-01 150.9
2 2005-02-01 151.6
3 2005-03-01 153.7
4 2005-04-01 155.0
... ... ...
198 2021-06-01 228.9
199 2021-07-01 231.2
200 2021-08-01 232.9
201 2021-09-01 235.4
202 2021-10-01 240.2

203 rows × 2 columns

The data set has a ppi entry for each month of the same period we use for the portfolio data.

3. DATA PREPARATION

For the portfoliio data we will only make use of the adjusted close price (‘Adj Close’). This form of the close price takes into account price changes due to, for example, stock splits and other management actions:

df_port = df_port['Adj Close']
df_port
FBCVX FCPGX FDSVX VBILX ^GSPC
Date
2004-12-01 8.920976 4.448220 7.593656 5.474646 1211.920044
2004-12-10 NaN NaN NaN NaN NaN
2004-12-17 NaN NaN NaN NaN NaN
2004-12-31 NaN NaN NaN NaN NaN
2005-01-01 8.871915 4.491105 7.228118 5.524208 1181.270020
... ... ... ... ... ...
2021-09-01 22.528105 28.668407 53.279999 12.092872 4307.540039
2021-09-03 NaN NaN NaN NaN NaN
2021-09-10 NaN NaN NaN NaN NaN
2021-10-01 23.780001 34.669998 57.630001 12.011015 4605.379883
2021-10-29 NaN NaN NaN NaN NaN

482 rows × 5 columns

Next, we will remove all the NaNs:

df_port = df_port.dropna()
df_port
FBCVX FCPGX FDSVX VBILX ^GSPC
Date
2004-12-01 8.920976 4.448220 7.593656 5.474646 1211.920044
2005-01-01 8.871915 4.491105 7.228118 5.524208 1181.270020
2005-02-01 9.171929 4.592466 7.228118 5.473928 1203.599976
2005-03-01 8.929062 4.545684 7.031666 5.416064 1180.589966
2005-04-01 8.657617 4.218208 6.936826 5.517607 1156.849976
... ... ... ... ... ...
2021-06-01 22.667166 32.630497 53.416515 12.096302 4297.500000
2021-07-01 22.955225 32.307598 54.362907 12.274221 4395.259766
2021-08-01 23.531340 34.271187 51.678432 12.233455 4522.680176
2021-09-01 22.528105 28.668407 53.279999 12.092872 4307.540039
2021-10-01 23.780001 34.669998 57.630001 12.011015 4605.379883

203 rows × 5 columns

We reset the index:

df_port = df_port.reset_index()
df_port
Date FBCVX FCPGX FDSVX VBILX ^GSPC
0 2004-12-01 8.920976 4.448220 7.593656 5.474646 1211.920044
1 2005-01-01 8.871915 4.491105 7.228118 5.524208 1181.270020
2 2005-02-01 9.171929 4.592466 7.228118 5.473928 1203.599976
3 2005-03-01 8.929062 4.545684 7.031666 5.416064 1180.589966
4 2005-04-01 8.657617 4.218208 6.936826 5.517607 1156.849976
... ... ... ... ... ... ...
198 2021-06-01 22.667166 32.630497 53.416515 12.096302 4297.500000
199 2021-07-01 22.955225 32.307598 54.362907 12.274221 4395.259766
200 2021-08-01 23.531340 34.271187 51.678432 12.233455 4522.680176
201 2021-09-01 22.528105 28.668407 53.279999 12.092872 4307.540039
202 2021-10-01 23.780001 34.669998 57.630001 12.011015 4605.379883

203 rows × 6 columns

The data set contains asset prices. We want to change this so that each entry contains the return of each asset relative to the previous month. We express these monthly returns as percentages:

# https://factorpad.com/fin/quant-101/calculate-stock-returns.html
n_months = len(df_port)
df_port2 = pd.DataFrame()
for i in range(1, n_months):
  df_port2 = df_port2.append({
      'Date': df_port.iloc[i,0],
      'FBCVX': 100*(df_port.iloc[i,1]/df_port.iloc[i-1,1] - 1), 
      'FCPGX': 100*(df_port.iloc[i,2]/df_port.iloc[i-1,2] - 1), 
      'FDSVX': 100*(df_port.iloc[i,3]/df_port.iloc[i-1,3] - 1), 
      'VBILX': 100*(df_port.iloc[i,4]/df_port.iloc[i-1,4] - 1), 
      '^GSPC': 100*(df_port.iloc[i,5]/df_port.iloc[i-1,5] - 1)}, ignore_index=True)
df_port2
Date FBCVX FCPGX FDSVX VBILX ^GSPC
0 2005-01-01 -0.549949 0.964090 -4.813724 0.905300 -2.529047
1 2005-02-01 3.381621 2.256945 0.000000 -0.910160 1.890335
2 2005-03-01 -2.647943 -1.018669 -2.717888 -1.057087 -1.911766
3 2005-04-01 -3.040020 -7.204108 -1.348757 1.874839 -2.010858
4 2005-05-01 2.970302 5.637682 3.613289 1.445314 2.995205
... ... ... ... ... ... ...
197 2021-06-01 -1.680311 4.005561 4.262883 0.743934 2.221401
198 2021-07-01 1.270822 -0.989562 1.771722 1.470858 2.274805
199 2021-08-01 2.509732 6.077792 -4.938064 -0.332133 2.899042
200 2021-09-01 -4.263399 -16.348367 3.099100 -1.149169 -4.756917
201 2021-10-01 5.557040 20.934510 8.164419 -0.676901 6.914384

202 rows × 6 columns

df_port2.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 202 entries, 0 to 201
Data columns (total 6 columns):
 #   Column  Non-Null Count  Dtype         
---  ------  --------------  -----         
 0   Date    202 non-null    datetime64[ns]
 1   FBCVX   202 non-null    float64       
 2   FCPGX   202 non-null    float64       
 3   FDSVX   202 non-null    float64       
 4   VBILX   202 non-null    float64       
 5   ^GSPC   202 non-null    float64       
dtypes: datetime64[ns](1), float64(5)
memory usage: 9.6 KB

For the inflation data set, we rename the column containing the inflation values. We also rename the DATE column to Date:

df_inf['inflation'] = df_inf['T10YIEM']
df_inf
DATE T10YIEM inflation
0 2004-12-01 2.56 2.56
1 2005-01-01 2.50 2.50
2 2005-02-01 2.54 2.54
3 2005-03-01 2.71 2.71
4 2005-04-01 2.63 2.63
... ... ... ...
199 2021-07-01 2.33 2.33
200 2021-08-01 2.35 2.35
201 2021-09-01 2.34 2.34
202 2021-10-01 2.53 2.53
203 2021-11-01 2.62 2.62

204 rows × 3 columns

df_inf = df_inf.drop('T10YIEM', axis=1)
df_inf = df_inf.rename(columns={"DATE": "Date"})
df_inf
Date inflation
0 2004-12-01 2.56
1 2005-01-01 2.50
2 2005-02-01 2.54
3 2005-03-01 2.71
4 2005-04-01 2.63
... ... ...
199 2021-07-01 2.33
200 2021-08-01 2.35
201 2021-09-01 2.34
202 2021-10-01 2.53
203 2021-11-01 2.62

204 rows × 2 columns

Finally, we change the data type of the Date column from string to datetime:

df_inf['Date'] = pd.to_datetime(df_inf['Date'])

Now on to the PPI data set. We rename the column containing the ppi values and again rename the DATE column to Date:

df_ppi['ppi'] = df_ppi['PPIACO']
df_ppi
DATE PPIACO ppi
0 2004-12-01 150.2 150.2
1 2005-01-01 150.9 150.9
2 2005-02-01 151.6 151.6
3 2005-03-01 153.7 153.7
4 2005-04-01 155.0 155.0
... ... ... ...
198 2021-06-01 228.9 228.9
199 2021-07-01 231.2 231.2
200 2021-08-01 232.9 232.9
201 2021-09-01 235.4 235.4
202 2021-10-01 240.2 240.2

203 rows × 3 columns

df_ppi = df_ppi.drop('PPIACO', axis=1)
df_ppi = df_ppi.rename(columns={"DATE": "Date"})
df_ppi
Date ppi
0 2004-12-01 150.2
1 2005-01-01 150.9
2 2005-02-01 151.6
3 2005-03-01 153.7
4 2005-04-01 155.0
... ... ...
198 2021-06-01 228.9
199 2021-07-01 231.2
200 2021-08-01 232.9
201 2021-09-01 235.4
202 2021-10-01 240.2

203 rows × 2 columns

Finally, we change the data type of the Date column from string to datetime:

df_ppi['Date'] = pd.to_datetime(df_ppi['Date'])

Finally, we need to merge the 3 data sets. First, we merge the portfolio and the inflation data sets:

dftmp = pd.merge(df_port2, df_inf)
dftmp
Date FBCVX FCPGX FDSVX VBILX ^GSPC inflation
0 2005-01-01 -0.549949 0.964090 -4.813724 0.905300 -2.529047 2.50
1 2005-02-01 3.381621 2.256945 0.000000 -0.910160 1.890335 2.54
2 2005-03-01 -2.647943 -1.018669 -2.717888 -1.057087 -1.911766 2.71
3 2005-04-01 -3.040020 -7.204108 -1.348757 1.874839 -2.010858 2.63
4 2005-05-01 2.970302 5.637682 3.613289 1.445314 2.995205 2.49
... ... ... ... ... ... ... ...
197 2021-06-01 -1.680311 4.005561 4.262883 0.743934 2.221401 2.34
198 2021-07-01 1.270822 -0.989562 1.771722 1.470858 2.274805 2.33
199 2021-08-01 2.509732 6.077792 -4.938064 -0.332133 2.899042 2.35
200 2021-09-01 -4.263399 -16.348367 3.099100 -1.149169 -4.756917 2.34
201 2021-10-01 5.557040 20.934510 8.164419 -0.676901 6.914384 2.53

202 rows × 7 columns

Now we merge this temporary data set with the ppi data set:

df3 = pd.merge(dftmp, df_ppi)
df3
Date FBCVX FCPGX FDSVX VBILX ^GSPC inflation ppi
0 2005-01-01 -0.549949 0.964090 -4.813724 0.905300 -2.529047 2.50 150.9
1 2005-02-01 3.381621 2.256945 0.000000 -0.910160 1.890335 2.54 151.6
2 2005-03-01 -2.647943 -1.018669 -2.717888 -1.057087 -1.911766 2.71 153.7
3 2005-04-01 -3.040020 -7.204108 -1.348757 1.874839 -2.010858 2.63 155.0
4 2005-05-01 2.970302 5.637682 3.613289 1.445314 2.995205 2.49 154.3
... ... ... ... ... ... ... ... ...
197 2021-06-01 -1.680311 4.005561 4.262883 0.743934 2.221401 2.34 228.9
198 2021-07-01 1.270822 -0.989562 1.771722 1.470858 2.274805 2.33 231.2
199 2021-08-01 2.509732 6.077792 -4.938064 -0.332133 2.899042 2.35 232.9
200 2021-09-01 -4.263399 -16.348367 3.099100 -1.149169 -4.756917 2.34 235.4
201 2021-10-01 5.557040 20.934510 8.164419 -0.676901 6.914384 2.53 240.2

202 rows × 8 columns

We write this prepared data set to the file MAB-data.csv:

df3.to_csv(base_dir+'MAB-data.csv', index=False)

Instead of the previous lengthy preparation, we can simply execute the following function to reload the data:

def load_market_data(file_name):
  return pd.read_csv(file_name)
DEFAULT_DATA_FILE = base_dir + "MAB-data.csv" #full path
df = load_market_data(DEFAULT_DATA_FILE)
df
Date FBCVX FCPGX FDSVX VBILX ^GSPC inflation ppi
0 2005-01-01 -0.549981 0.964068 -4.813760 0.905283 -2.529047 2.50 150.9
1 2005-02-01 3.381654 2.256945 0.000000 -0.910186 1.890335 2.54 151.6
2 2005-03-01 -2.647933 -1.018689 -2.717901 -1.057027 -1.911766 2.71 153.7
3 2005-04-01 -3.040052 -7.204110 -1.348777 1.874751 -2.010858 2.63 155.0
4 2005-05-01 2.970291 5.637717 3.613303 1.445384 2.995205 2.49 154.3
... ... ... ... ... ... ... ... ...
197 2021-06-01 -1.680311 4.005561 4.262883 0.743950 2.221401 2.34 228.9
198 2021-07-01 1.270822 -0.989562 1.771722 1.470834 2.274805 2.33 231.2
199 2021-08-01 2.509732 6.077792 -4.938064 -0.332125 2.899042 2.35 232.9
200 2021-09-01 -4.263399 -16.348367 3.099100 -1.149169 -4.756917 2.34 235.4
201 2021-10-01 5.557040 20.934510 8.164419 -0.676901 6.914384 2.53 240.2

202 rows × 8 columns

4. MODELING

Let’s look at some decriptive statistics for each column of this final data set:

df.describe()
FBCVX FCPGX FDSVX VBILX ^GSPC inflation ppi
count 202.000000 202.000000 202.000000 202.000000 202.000000 202.000000 202.000000
mean 0.604243 1.212826 1.121308 0.399683 0.753228 2.026980 190.473762
std 4.805495 6.164501 4.741958 1.418614 4.224650 0.410852 16.571523
min -18.695924 -23.583340 -18.697137 -4.225292 -16.942452 0.250000 150.900000
25% -1.756639 -1.992111 -1.518301 -0.388497 -1.505970 1.770000 181.000000
50% 1.129390 1.520422 1.477411 0.427129 1.239402 2.120000 193.550000
75% 3.416452 5.109637 3.978763 1.237308 3.146408 2.337500 201.975000
max 13.170427 20.934510 14.879392 5.735699 12.684404 2.710000 240.200000

Being armed with historical data, it will be interesting to discover the range of performance possibilities. For example, say we deliberately invest each month in the worst performing asset. What would the end result be? Similarly, if we invest repreatedly in the best performing asset each month, what would the return be?

n_months = len(df)
n_years = n_months/12
n_months, n_years
(202, 16.833333333333332)

Our data set covers a timespan of 202 months or about 17 years. To calculate the average montly return in the worst as well as the best case scenarios, we do:

DEFAULT_TICKERS = ["FBCVX", "FCPGX", "FDSVX", "VBILX", "^GSPC"]
n_months = len(df)
min_list = []
max_list = []
for i in range(n_months):
    row = df.iloc[i, 1:len(DEFAULT_TICKERS)+1]
    min_list.append(min(row)) # worst performer for month i
    max_list.append(max(row)) # best performer for month i
avg_min = sum(min_list)/n_months
avg_max = sum(max_list)/n_months
avg_min_annualized = 12*avg_min
avg_max_annualized = 12*avg_max
print(f"{avg_min:5.2f}% Average monthly worst case")
print(f"{avg_max:5.2f}% Average monthly best case\n")
print(f"{avg_min_annualized:5.2f}% Average annual worst case")
print(f"{avg_max_annualized:5.2f}% Average annual best case")
-2.30% Average monthly worst case
 3.95% Average monthly best case

-27.55% Average annual worst case
47.38% Average annual best case

Next we prepare a dataframe that has the worst and best returns (among the 5 assets) for each month:

min_max = pd.DataFrame.from_dict({'Month': df['Date'], 'min':min_list, 'max':max_list})
min_max
Month min max
0 2005-01-01 -4.813760 0.964068
1 2005-02-01 -0.910186 3.381654
2 2005-03-01 -2.717901 -1.018689
3 2005-04-01 -7.204110 1.874751
4 2005-05-01 1.445384 5.637717
... ... ... ...
197 2021-06-01 -1.680311 4.262883
198 2021-07-01 -0.989562 2.274805
199 2021-08-01 -4.938064 6.077792
200 2021-09-01 -16.348367 3.099100
201 2021-10-01 -0.676901 20.934510

202 rows × 3 columns

This can be visualized as follows:

fig,axs = plt.subplots(figsize=(14,10))
axs.set_xlabel('Months', fontsize=20)
axs.set_ylabel('Monthly Return (%)', fontsize=20)
axs.set_title(f'Best vs Worst Monthly Return over 202 months ({202/12:2.0f} years)', fontsize=24)
axs.fill_between(df["Date"], min_list, max_list,color="g", alpha=0.5)
axs.xaxis.set_major_locator(plt.AutoLocator())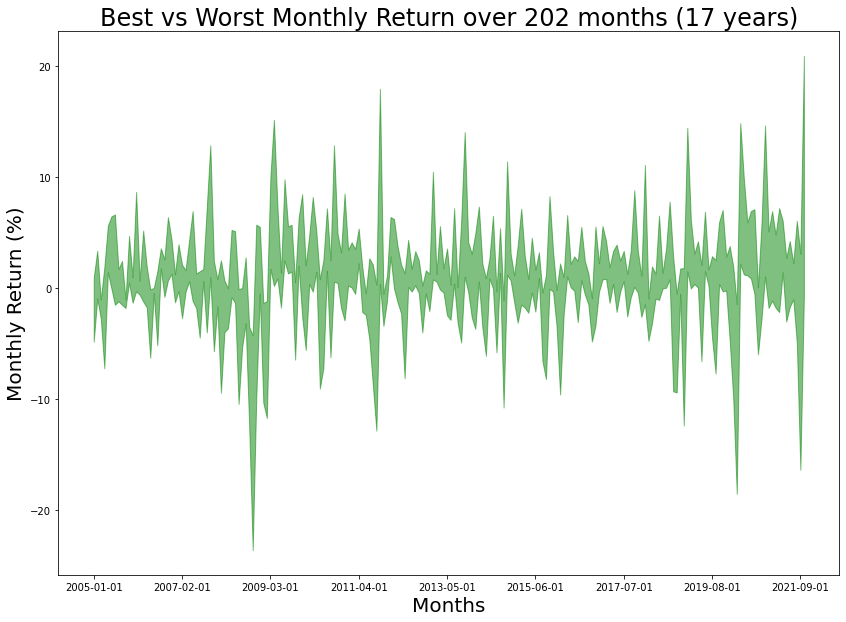

For some months where the performance varies widely, while for other months all assets have about the same performance.

fig,axs = plt.subplots(figsize=(14,10))
axs.set_xlabel('Months', fontsize=20)
axs.set_ylabel('Monthly Return (%)', fontsize=20)
axs.set_title(f'Best vs Worst Accumulated Monthly Return over 202 months ({202/12:2.0f} years)', fontsize=24)
axs.fill_between(df["Date"], min_list, max_list,color="g",alpha=0.5)
axs.xaxis.set_major_locator(plt.AutoLocator())
axs.plot(min_max['min'].cumsum(), color='k', label='Worst case', linestyle='-.')
axs.plot(min_max['max'].cumsum(), color='k', label='Best case', linestyle='--')
axs.legend(fontsize=20);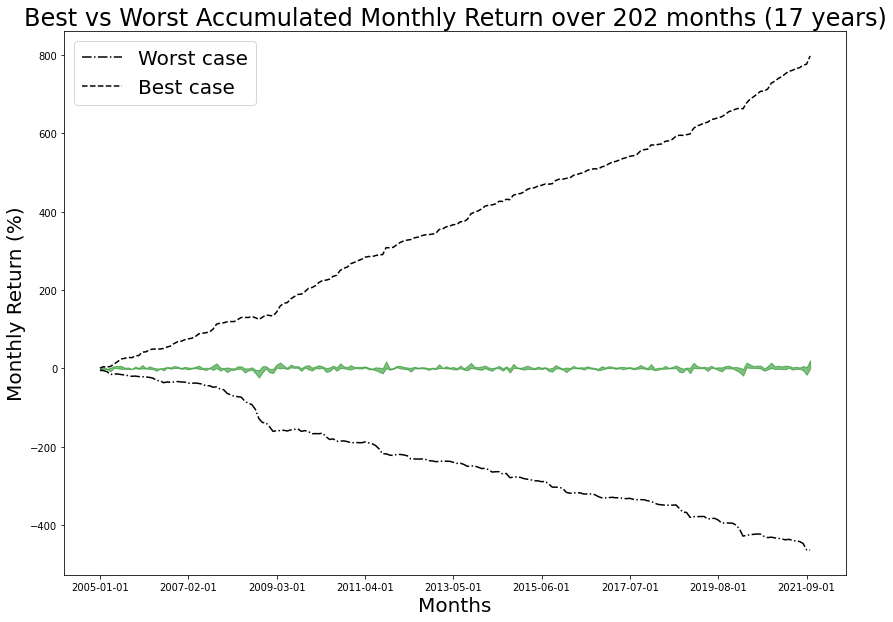

Multi-Armed Bandits

Multi-armed bandits (MABs) are named after slot machines in casinos (a.k.a., one-armed bandits). The term bandits is often used and could refer to single-arms as well as multi-armed bandits. When an arm is pulled, a probabilistically determined cash payout is (sometimes) produced for a reward. Often a MAB implementation has multiple, say N, “arms”. Each arm represent one of N possible actions an agent can take at a given time step. In the case of our present problem N=4, i.e. an action for each of the events where all funds are invested in one of the 5 assets.

In their simplest form, bandits have the following two restrictions in relation to general reinforcement learning:

  • The state spaces of MABs are stationary or evolves slowly. Bandits do not attempt to learn the best actions for more than one state.
  • Each action that is taken by the agent does not affect the next state of the environment - it only affects the reward received. In the case of reinforcement learning (which is based on a Markov Decision Process) the action taken by the agent partly determines the next state of the environment.

Contextual Multi-Armed Bandits

In the case of contextual bandits the state of the environment (called the context) is considered and has an influence on the decisions that are made. Consequently the first restriction described above is relaxed. The MAB algorithm observes the context (state) at each time step and uses this information to choose the next action to take. It then observes the reward for the action.

The relaxation of the first restriction brings the operation of MABs closer to that of reinforcement learning. However, the second restriction remains meaning that the state is not influenced by the action taken.

Reward and Regret

Instead of having the MAB algorithm maximize rewards things can also be arranged such that the regret is modeled. Regret is the difference between the actual reward and the best possible reward (i.e. choosing the best decision at each step).

The MAB cannot predict rewards accurately. Of course, the reason for using a MAB is to try to maximize the average reward. If the MAB had perfect insight it would always choose the arm with the highest average reward so that the eventual cumulative reward would be maximized. It is necessary for a MAB to strike a balance between exploitation and exploration.

For our problem at hand in this POC the context is represented by the investment market conditions. In this POC we use the monthly inflation and the monthly PPI to represent these conditions (in the final results the use of PPI has been dropped). The “arm” that is pulled by the agent determines the asset into which all the funds are moved for the current month. The reward is determined by the subsequent performance of the selected asset. The regret is the difference between the reward and the subsequent performance of the best-performing asset for the current month.

Model

Investment decisions are sequential by nature. To model the situation requires the setup of a digital twin for the investor’s portfolio. This model of the portfolio is called an environment. The environment contains states and actions are applied to the environment by the agent.

We will choose the following state vector (measured monthly in our case) for the environment (note that the state is called the context when MABs are involved):

\[ \Large \begin{aligned} s_1 &= \text{Value of inflation this month} \\ s_2 &= \text{Value of PPI this month} \end{aligned} \]

The following action vector (applied monthly in our case) will be setup:

\[ \Large \begin{aligned} a_1 &= \text{Funds to be invested in FBCVX this cycle} \\ a_2 &= \text{Funds to be invested in FCPGX this cycle} \\ a_3 &= \text{Funds to be invested in FDSVX this cycle} \\ a_4 &= \text{Funds to be invested in VBILX this cycle} \\ a_5 &= \text{Funds to be invested in GSPC this cycle} \end{aligned} \]

All action values are either 0 or 1. The “arm” that is “pulled” is a 1 and all other “arms” are 0.

The reward r is the subsequent return of the selected asset over that month.

Environment

We make use of the OpenAI Gym framework to define and setup an environment. Then we will train a contextual MAB to optimize monthly investments.

!pip install gym==0.17.3
import gym
gym.__version__
Requirement already satisfied: gym==0.17.3 in /usr/local/lib/python3.7/dist-packages (0.17.3)
Requirement already satisfied: cloudpickle<1.7.0,>=1.2.0 in /usr/local/lib/python3.7/dist-packages (from gym==0.17.3) (1.3.0)
Requirement already satisfied: scipy in /usr/local/lib/python3.7/dist-packages (from gym==0.17.3) (1.4.1)
Requirement already satisfied: numpy>=1.10.4 in /usr/local/lib/python3.7/dist-packages (from gym==0.17.3) (1.19.5)
Requirement already satisfied: pyglet<=1.5.0,>=1.4.0 in /usr/local/lib/python3.7/dist-packages (from gym==0.17.3) (1.5.0)
Requirement already satisfied: future in /usr/local/lib/python3.7/dist-packages (from pyglet<=1.5.0,>=1.4.0->gym==0.17.3) (0.16.0)
'0.17.3'
from gym.spaces import Discrete, Box
from gym.utils import seeding
import random
# hide
df.index.max()
201
DEFAULT_MIN_INFLATION = -100.0
DEFAULT_MAX_INFLATION = 100.0
DEFAULT_MIN_PPI = -250.0
DEFAULT_MAX_PPI = 250.0
SAVE_DIR = f"{base_dir}RLlib-MAB-Trader_SAVED"
class MarketBandit (gym.Env):    
    def __init__ (self, config={}):
        self.min_inflation = config.get("min-inflation", DEFAULT_MIN_INFLATION)
        self.max_inflation = config.get("max-inflation", DEFAULT_MAX_INFLATION)
        self.min_ppi = config.get("min-ppi", DEFAULT_MIN_PPI)
        self.max_ppi = config.get("max-ppi", DEFAULT_MAX_PPI)
        self.tickers = config.get("tickers", DEFAULT_TICKERS)
        self.data_file = config.get("data-file", DEFAULT_DATA_FILE)
        print(f"MarketBandit: min_inflation: {self.min_inflation}, max_inflation: {self.max_inflation}, min_ppi: {self.min_ppi}, max_ppi: {self.max_ppi}, tickers: {self.tickers}, data file: {self.data_file} (config: {config})")
        self.action_space = Discrete(len(DEFAULT_TICKERS)-1) #FBCVX FCPGX   FDSVX   VBILX   ^GSPC
        # self.observation_space = Box(low=self.min_obs, high=self.max_obs, shape=(1,))
        # self.observation_space = Box(low=np.array((self.min_inflation, self.min_ppi)), high=np.array((self.max_inflation, self.max_ppi)), shape=(2,))
        self.observation_space = Box(low=np.array((self.min_inflation,)), high=np.array((self.max_inflation,)), shape=(1,))
        # self.observation_space = Box(low=np.array((self.min_ppi,)), high=np.array((self.max_ppi,)), shape=(1,))
        self.df = load_market_data(self.data_file)
        self.cur_context = None

    def reset (self):
        self.month = 0
        # self.cur_context = self.df.loc[0]["inflation"] #first value of inflation
        # self.cur_context = np.array((df.iloc[0]['inflation'],df.iloc[0]['ppi']), dtype=np.float32) #first value of inflation and ppi
        self.cur_context = np.array((df.iloc[0]['inflation'],), dtype=np.float32) #first value of inflation
        # self.cur_context = np.array((df.iloc[0]['ppi'],), dtype=np.float32) #first value of ppi
        self.done = False
        self.info = {}
        return self.cur_context

    def step (self, action):
        if self.done:
            reward = 0. 
            regret = 0.
        else:
            row = self.df.loc[self.month]

            # calculate reward
            ticker = self.tickers[action] #. invested in this ticker
            reward = float(row[ticker]) #. return for ticker in self.month

            # calculate regret
            max_reward = max(map(lambda t: float(row[t]), self.tickers)) #. max return for self.month
            regret = max_reward - reward

            # update the context
            # self.cur_context = float(row["inflation"])
            # self.cur_context = np.array((float(row["inflation"]),float(row["ppi"])), dtype=np.float32)
            self.cur_context = np.array((float(row["inflation"]),), dtype=np.float32)
            # self.cur_context = np.array((float(row["ppi"]),), dtype=np.float32)

            # increment the month
            self.month += 1

            if self.month >= self.df.index.max():
                self.done = True

        context = self.cur_context
        self.info = {"regret": regret, "month": self.month}
        return context, reward, self.done, self.info

    def seed (self, seed=None):
        """Sets the seed for this env's random number generator(s).
        Note:
            Some environments use multiple pseudorandom number generators.
            We want to capture all such seeds used in order to ensure that
            there aren't accidental correlations between multiple generators.
        Returns:
            list<bigint>: Returns the list of seeds used in this env's random
              number generators. The first value in the list should be the
              "main" seed, or the value which a reproducer should pass to
              'seed'. Often, the main seed equals the provided 'seed', but
              this won't be true if seed=None, for example.
        """
        self.np_random, seed=seeding.np_random(seed)
        return [seed]

Let’s exercise this bandit to see how it behaves. Every timestep we draw a random action and apply it to the environment:

bandit = MarketBandit()
bandit.reset()
for i in range(20):
    action = bandit.action_space.sample()
    obs = bandit.step(action) #. context (inflation), reward (monthly return), done, info
    print(action, obs)
MarketBandit: min_inflation: -100.0, max_inflation: 100.0, min_ppi: -250.0, max_ppi: 250.0, tickers: ['FBCVX', 'FCPGX', 'FDSVX', 'VBILX', '^GSPC'], data file: /content/gdrive/My Drive/RLlib/MAB-data.csv (config: {})
1 (array([2.5], dtype=float32), 0.9640680080976738, False, {'regret': 0.0, 'month': 1})
1 (array([2.54], dtype=float32), 2.2569447946701566, False, {'regret': 1.12470908992508, 'month': 2})
2 (array([2.71], dtype=float32), -2.7179007055068367, False, {'regret': 1.6992112515503806, 'month': 3})
2 (array([2.63], dtype=float32), -1.3487768464212957, False, {'regret': 3.2235274145295367, 'month': 4})
2 (array([2.49], dtype=float32), 3.613303248135869, False, {'regret': 2.0244141864932836, 'month': 5})
1 (array([2.33], dtype=float32), 6.474183320675863, False, {'regret': 0.0, 'month': 6})
3 (array([2.3], dtype=float32), -1.488956564169075, False, {'regret': 8.144654338108982, 'month': 7})
1 (array([2.37], dtype=float32), -0.6933626832149264, False, {'regret': 2.4301268824369004, 'month': 8})
1 (array([2.5], dtype=float32), -0.6981942786783879, False, {'regret': 3.1578439684864845, 'month': 9})
1 (array([2.52], dtype=float32), -1.1413245289026321, False, {'regret': 0.15826534519037838, 'month': 10})
2 (array([2.48], dtype=float32), 2.9783312877532886, False, {'regret': 1.7357480656293278, 'month': 11})
3 (array([2.35], dtype=float32), 0.9841181103575458, False, {'regret': 0.0, 'month': 12})
0 (array([2.41], dtype=float32), 6.218444769962118, False, {'regret': 2.4702203899120247, 'month': 13})
0 (array([2.52], dtype=float32), -0.4954265125803437, False, {'regret': 1.172787211070636, 'month': 14})
2 (array([2.52], dtype=float32), 2.85956951304831, False, {'regret': 2.338976333394749, 'month': 15})
1 (array([2.58], dtype=float32), -0.13723775391654147, False, {'regret': 2.1021183278173483, 'month': 16})
0 (array([2.66], dtype=float32), -3.78526357679021, False, {'regret': 3.695851839865427, 'month': 17})
0 (array([2.58], dtype=float32), -0.4291917187929095, False, {'regret': 0.45857045625100623, 'month': 18})
0 (array([2.58], dtype=float32), 0.21554897459590272, False, {'regret': 1.3245879156507545, 'month': 19})
2 (array([2.59], dtype=float32), 3.6051419905896336, False, {'regret': 0.0, 'month': 20})
/usr/local/lib/python3.7/dist-packages/gym/logger.py:30: UserWarning: WARN: Box bound precision lowered by casting to float32
  warnings.warn(colorize('%s: %s'%('WARN', msg % args), 'yellow'))

It is also handy to use this environment in a type of monte carlo simulation. This establishes a baseline for what the rewards would be if purely random actions are selected.

done = 1
reward_list = []
iterations = 10000
# iterations = 50000
for i in range(iterations):
    if done == 1:
        bandit.reset()
    action = bandit.action_space.sample()
    obs = bandit.step(action)
    context, reward, done, info = obs
    reward_list.append(reward)
    # print(action, context, reward, done, info)
df_mc = pd.DataFrame(reward_list, columns=["reward"])
df_mc.head()
reward
0 -4.813760
1 -0.910186
2 -1.057027
3 -7.204110
4 2.970291 
df_mc.mean()
reward    0.794577
dtype: float64

Recall that we found the following earlier:

print(f"{avg_min:5.2f}% Average monthly worst case")
print(f"{avg_max:5.2f}% Average monthly best case\n")
print(f"{avg_min_annualized:5.2f}% Average annual worst case")
print(f"{avg_max_annualized:5.2f}% Average annual best case")
-2.30% Average monthly worst case
 3.95% Average monthly best case

-27.55% Average annual worst case
47.38% Average annual best case

We expect the monte carlo average reward (0.79%) to be more than the average monthly worst case of -2.30% – and indeed it is! Of course, it also needs to be less than the average monthly best case of 3.95%. The visualization of the monte carlo simulation shows its randomness and total lack of learning behavior:

df_mc.plot(y="reward", title="Reward Over Iterations", figsize=(10,6));

Agent

Next we will train an agent using Linear Thompson Sampling making use of the Ray RLlib framework. Our expectation is that it will do better than the random results from the monte carlo simulation. Let’s install the RLlib library:

!pip install ray[rllib]
# import ray
# ray.__version__
Requirement already satisfied: ray[rllib] in /usr/local/lib/python3.7/dist-packages (1.9.0)
Requirement already satisfied: jsonschema in /usr/local/lib/python3.7/dist-packages (from ray[rllib]) (2.6.0)
Requirement already satisfied: filelock in /usr/local/lib/python3.7/dist-packages (from ray[rllib]) (3.4.0)
Requirement already satisfied: msgpack<2.0.0,>=1.0.0 in /usr/local/lib/python3.7/dist-packages (from ray[rllib]) (1.0.3)
Requirement already satisfied: pyyaml in /usr/local/lib/python3.7/dist-packages (from ray[rllib]) (3.13)
Requirement already satisfied: grpcio>=1.28.1 in /usr/local/lib/python3.7/dist-packages (from ray[rllib]) (1.42.0)
Requirement already satisfied: attrs in /usr/local/lib/python3.7/dist-packages (from ray[rllib]) (21.2.0)
Requirement already satisfied: click>=7.0 in /usr/local/lib/python3.7/dist-packages (from ray[rllib]) (7.1.2)
Requirement already satisfied: redis>=3.5.0 in /usr/local/lib/python3.7/dist-packages (from ray[rllib]) (4.0.2)
Requirement already satisfied: numpy>=1.16 in /usr/local/lib/python3.7/dist-packages (from ray[rllib]) (1.19.5)
Requirement already satisfied: protobuf>=3.15.3 in /usr/local/lib/python3.7/dist-packages (from ray[rllib]) (3.17.3)
Requirement already satisfied: matplotlib!=3.4.3 in /usr/local/lib/python3.7/dist-packages (from ray[rllib]) (3.2.2)
Requirement already satisfied: tabulate in /usr/local/lib/python3.7/dist-packages (from ray[rllib]) (0.8.9)
Requirement already satisfied: lz4 in /usr/local/lib/python3.7/dist-packages (from ray[rllib]) (3.1.10)
Requirement already satisfied: gym in /usr/local/lib/python3.7/dist-packages (from ray[rllib]) (0.17.3)
Requirement already satisfied: requests in /usr/local/lib/python3.7/dist-packages (from ray[rllib]) (2.23.0)
Requirement already satisfied: scipy in /usr/local/lib/python3.7/dist-packages (from ray[rllib]) (1.4.1)
Requirement already satisfied: dm-tree in /usr/local/lib/python3.7/dist-packages (from ray[rllib]) (0.1.6)
Requirement already satisfied: scikit-image in /usr/local/lib/python3.7/dist-packages (from ray[rllib]) (0.18.3)
Requirement already satisfied: pandas in /usr/local/lib/python3.7/dist-packages (from ray[rllib]) (1.1.5)
Requirement already satisfied: tensorboardX>=1.9 in /usr/local/lib/python3.7/dist-packages (from ray[rllib]) (2.4.1)
Requirement already satisfied: six>=1.5.2 in /usr/local/lib/python3.7/dist-packages (from grpcio>=1.28.1->ray[rllib]) (1.15.0)
Requirement already satisfied: python-dateutil>=2.1 in /usr/local/lib/python3.7/dist-packages (from matplotlib!=3.4.3->ray[rllib]) (2.8.2)
Requirement already satisfied: cycler>=0.10 in /usr/local/lib/python3.7/dist-packages (from matplotlib!=3.4.3->ray[rllib]) (0.11.0)
Requirement already satisfied: pyparsing!=2.0.4,!=2.1.2,!=2.1.6,>=2.0.1 in /usr/local/lib/python3.7/dist-packages (from matplotlib!=3.4.3->ray[rllib]) (3.0.6)
Requirement already satisfied: kiwisolver>=1.0.1 in /usr/local/lib/python3.7/dist-packages (from matplotlib!=3.4.3->ray[rllib]) (1.3.2)
Requirement already satisfied: deprecated in /usr/local/lib/python3.7/dist-packages (from redis>=3.5.0->ray[rllib]) (1.2.13)
Requirement already satisfied: wrapt<2,>=1.10 in /usr/local/lib/python3.7/dist-packages (from deprecated->redis>=3.5.0->ray[rllib]) (1.13.3)
Requirement already satisfied: pyglet<=1.5.0,>=1.4.0 in /usr/local/lib/python3.7/dist-packages (from gym->ray[rllib]) (1.5.0)
Requirement already satisfied: cloudpickle<1.7.0,>=1.2.0 in /usr/local/lib/python3.7/dist-packages (from gym->ray[rllib]) (1.3.0)
Requirement already satisfied: future in /usr/local/lib/python3.7/dist-packages (from pyglet<=1.5.0,>=1.4.0->gym->ray[rllib]) (0.16.0)
Requirement already satisfied: pytz>=2017.2 in /usr/local/lib/python3.7/dist-packages (from pandas->ray[rllib]) (2018.9)
Requirement already satisfied: urllib3!=1.25.0,!=1.25.1,<1.26,>=1.21.1 in /usr/local/lib/python3.7/dist-packages (from requests->ray[rllib]) (1.24.3)
Requirement already satisfied: idna<3,>=2.5 in /usr/local/lib/python3.7/dist-packages (from requests->ray[rllib]) (2.10)
Requirement already satisfied: certifi>=2017.4.17 in /usr/local/lib/python3.7/dist-packages (from requests->ray[rllib]) (2021.10.8)
Requirement already satisfied: chardet<4,>=3.0.2 in /usr/local/lib/python3.7/dist-packages (from requests->ray[rllib]) (3.0.4)
Requirement already satisfied: PyWavelets>=1.1.1 in /usr/local/lib/python3.7/dist-packages (from scikit-image->ray[rllib]) (1.2.0)
Requirement already satisfied: networkx>=2.0 in /usr/local/lib/python3.7/dist-packages (from scikit-image->ray[rllib]) (2.6.3)
Requirement already satisfied: imageio>=2.3.0 in /usr/local/lib/python3.7/dist-packages (from scikit-image->ray[rllib]) (2.4.1)
Requirement already satisfied: tifffile>=2019.7.26 in /usr/local/lib/python3.7/dist-packages (from scikit-image->ray[rllib]) (2021.11.2)
Requirement already satisfied: pillow!=7.1.0,!=7.1.1,>=4.3.0 in /usr/local/lib/python3.7/dist-packages (from scikit-image->ray[rllib]) (7.1.2)

In the __init__() method for MarketBandit we set some parameters from the passed in config object. We need to create a custom config object with our parameters, by building on the default TS_CONFIG object for LinTS:

import copy
from ray.rllib.contrib.bandits.agents.lin_ts import TS_CONFIG
market_config = copy.deepcopy(TS_CONFIG)
market_config["env"] = MarketBandit
market_config["min-inflation"] = DEFAULT_MIN_INFLATION;
market_config["max-inflation"] = DEFAULT_MAX_INFLATION;
market_config["min-ppi"] = DEFAULT_MIN_PPI;
market_config["max-ppi"] = DEFAULT_MAX_PPI;
market_config["tickers"] = DEFAULT_TICKERS;
market_config["data-file"] = DEFAULT_DATA_FILE;

We’ll also define a custom trainer, which builds on the LinTSTrainer with “updates”. This will be the first argument that we’ll pass to ray.tune.run() later.

Note: if all we needed was the default LinTSTrainer trainer, (i.e. with no customized config settings), we could instead just pass the string "contrib/LinTS" to ray.tune.run().

from ray.rllib.contrib.bandits.agents.lin_ts import LinTSTrainer
import ray
ray.init(ignore_reinit_error=True)
2021-12-07 20:23:30,454 INFO worker.py:853 -- Calling ray.init() again after it has already been called.
MarketLinTSTrainer = LinTSTrainer.with_updates(
    name="MarketLinTSTrainer",
    default_config=market_config,      #merged with Trainer.COMMON_CONFIG (rllib/agent/trainer.py)
    #default_policy=[somePolicyClass]  #in case we had a policy...
)
# hide
# analysis = ray.tune.run(
#     run_or_experiment=,
#     name=None,
#     metric=None,
#     mode=None,
#     stop=None,
#     time_budget_s=None,
#     config=None,
#     resources_per_trial=None,
#     num_samples=1,
#     local_dir=None,
#     search_alg=None,
#     scheduler=None,
#     keep_checkpoints_num=None,
#     checkpoint_score_attr=None,
#     checkpoint_freq=0,
#     checkpoint_at_end=False,
#     verbose=Verbosity.V3_TRIAL_DETAILS,
#     progress_reporter=None,
#     log_to_file=False,
#     trial_name_creator=None,
#     trial_dirname_creator=None,
#     sync_config=None,
#     export_formats=None,
#     max_failures=0,
#     fail_fast=False,
#     restore=None,
#     server_port=None,
#     resume=False,
#     reuse_actors=False,
#     trial_executor=None,
#     raise_on_failed_trial=True,
#     callbacks=None,
#     max_concurrent_trials=None,
#     queue_trials=None,
#     loggers=None,
#     _remote=None)
analysis = ray.tune.run(
    MarketLinTSTrainer,
    config=market_config,
    mode='max',
    stop={"training_iteration": 200},
    num_samples=3,
    local_dir=SAVE_DIR,
    checkpoint_at_end=True,
    verbose=1,
)
== Status ==
Current time: 2021-12-07 20:32:19 (running for 00:04:13.74)
Memory usage on this node: 2.0/12.7 GiB
Using FIFO scheduling algorithm.
Resources requested: 0/2 CPUs, 0/0 GPUs, 0.0/6.99 GiB heap, 0.0/3.5 GiB objects
Result logdir: /content/gdrive/My Drive/RLlib/RLlib-MAB-Trader_SAVED/MarketLinTSTrainer_2021-12-07_20-28-06
Number of trials: 3/3 (3 TERMINATED)

2021-12-07 20:32:20,120 INFO tune.py:626 -- Total run time: 254.00 seconds (253.66 seconds for the tuning loop).
checkpoint_paths = analysis.get_trial_checkpoints_paths(
    trial=analysis.get_best_trial('episode_reward_mean'),
    metric='episode_reward_mean'
)
checkpoint_paths
[('/content/gdrive/My Drive/RLlib/RLlib-MAB-Trader_SAVED/MarketLinTSTrainer_2021-12-07_20-28-06/MarketLinTSTrainer_MarketBandit_2f4b3_00002_2_2021-12-07_20-28-21/checkpoint_000200/checkpoint-200',
  174.41112617206056)]
checkpoint_path = checkpoint_paths[0][0]
checkpoint_path
'/content/gdrive/My Drive/RLlib/RLlib-MAB-Trader_SAVED/MarketLinTSTrainer_2021-12-07_20-28-06/MarketLinTSTrainer_MarketBandit_2f4b3_00002_2_2021-12-07_20-28-21/checkpoint_000200/checkpoint-200'
stats = analysis.stats()
secs = stats["timestamp"] - stats["start_time"]
print(f'{secs:7.2f} seconds, {secs/60.0:7.2f} minutes')
 243.77 seconds,    4.06 minutes

Analyze the results

Let’s analyze the rewards and cumulative regrets from these trials.

df_ts = pd.DataFrame()
for key, df_trial in analysis.trial_dataframes.items():
    # print('key:', key, '\ndf_trial:', df_trial)
    df_ts = df_ts.append(df_trial, ignore_index=True)
# df_ts.head()
# df_ts
df_ts.columns
Index(['episode_reward_max', 'episode_reward_min', 'episode_reward_mean',
       'episode_len_mean', 'episodes_this_iter', 'num_healthy_workers',
       'timesteps_total', 'timesteps_this_iter', 'agent_timesteps_total',
       'done', 'episodes_total', 'training_iteration', 'trial_id',
       'experiment_id', 'date', 'timestamp', 'time_this_iter_s',
       'time_total_s', 'pid', 'hostname', 'node_ip', 'time_since_restore',
       'timesteps_since_restore', 'iterations_since_restore',
       'hist_stats/episode_reward', 'hist_stats/episode_lengths',
       'timers/sample_time_ms', 'timers/sample_throughput',
       'timers/load_time_ms', 'timers/load_throughput', 'timers/learn_time_ms',
       'timers/learn_throughput', 'info/num_steps_sampled',
       'info/num_agent_steps_sampled', 'info/num_steps_trained',
       'info/num_agent_steps_trained', 'perf/cpu_util_percent',
       'perf/ram_util_percent',
       'info/learner/default_policy/learner_stats/cumulative_regret',
       'info/learner/default_policy/learner_stats/update_latency'],
      dtype='object')
rewards = df_ts \
    .groupby("info/num_steps_trained")["episode_reward_mean"] \
    .aggregate(["mean", "max", "min", "std"])
rewards
mean max min std
info/num_steps_trained
100 NaN NaN NaN NaN
200 NaN NaN NaN NaN
300 187.331470 245.709469 83.732737 89.960000
400 187.331470 245.709469 83.732737 89.960000
500 196.738809 209.898217 175.570641 18.512179
... ... ... ... ...
19600 171.464961 174.801868 169.366441 2.921672
19700 171.619078 174.439291 169.477306 2.549615
19800 171.619078 174.439291 169.477306 2.549615
19900 171.390596 174.411126 168.949148 2.776653
20000 171.390596 174.411126 168.949148 2.776653

200 rows × 4 columns

rewards2 = rewards.dropna()
rewards2
mean max min std
info/num_steps_trained
300 187.331470 245.709469 83.732737 89.960000
400 187.331470 245.709469 83.732737 89.960000
500 196.738809 209.898217 175.570641 18.512179
600 196.738809 209.898217 175.570641 18.512179
700 180.336412 188.741837 169.126517 10.103910
... ... ... ... ...
19600 171.464961 174.801868 169.366441 2.921672
19700 171.619078 174.439291 169.477306 2.549615
19800 171.619078 174.439291 169.477306 2.549615
19900 171.390596 174.411126 168.949148 2.776653
20000 171.390596 174.411126 168.949148 2.776653

198 rows × 4 columns

rewards.plot(y=["mean", "max"], secondary_y=True, title="Rewards vs. Steps", figsize=(10,4));

df_ts.columns
Index(['episode_reward_max', 'episode_reward_min', 'episode_reward_mean',
       'episode_len_mean', 'episodes_this_iter', 'num_healthy_workers',
       'timesteps_total', 'timesteps_this_iter', 'agent_timesteps_total',
       'done', 'episodes_total', 'training_iteration', 'trial_id',
       'experiment_id', 'date', 'timestamp', 'time_this_iter_s',
       'time_total_s', 'pid', 'hostname', 'node_ip', 'time_since_restore',
       'timesteps_since_restore', 'iterations_since_restore',
       'hist_stats/episode_reward', 'hist_stats/episode_lengths',
       'timers/sample_time_ms', 'timers/sample_throughput',
       'timers/load_time_ms', 'timers/load_throughput', 'timers/learn_time_ms',
       'timers/learn_throughput', 'info/num_steps_sampled',
       'info/num_agent_steps_sampled', 'info/num_steps_trained',
       'info/num_agent_steps_trained', 'perf/cpu_util_percent',
       'perf/ram_util_percent',
       'info/learner/default_policy/learner_stats/cumulative_regret',
       'info/learner/default_policy/learner_stats/update_latency'],
      dtype='object')
regrets = df_ts \
    .groupby("info/num_steps_trained")["info/learner/default_policy/learner_stats/cumulative_regret"] \
    .aggregate(["mean", "max", "min", "std"])
regrets
mean max min std
info/num_steps_trained
100 299.824804 337.455497 274.296108 33.273426
200 584.055773 688.692582 523.601620 90.982618
300 880.285545 977.316484 827.512870 84.139029
400 1145.124313 1202.205894 1107.693359 50.227136
500 1448.820851 1457.059286 1438.845078 9.230552
... ... ... ... ...
19600 59001.838455 59197.373074 58692.813072 270.749541
19700 59300.200660 59506.360391 59028.120609 245.840271
19800 59616.779957 59840.733870 59353.851804 245.769771
19900 59925.446903 60170.497431 59625.497795 276.616234
20000 60255.059771 60474.302171 60000.789844 238.691593

200 rows × 4 columns

regrets.plot(y="mean", yerr="std", title="Regrets vs. Steps", figsize=(10,12));

5. EVALUATION

Let’s assess how well did the trained policy perform. The results should be better than random monte carlo simulation. At the same time, the performance should be less than the best case.

Once again we summarise some previous results:

print(f"{avg_min:5.2f}% Average monthly worst case")
print(f"{avg_max:5.2f}% Average monthly best case\n")
print(f"{avg_min_annualized:5.2f}% Average annual worst case")
print(f"{avg_max_annualized:5.2f}% Average annual best case")
-2.30% Average monthly worst case
 3.95% Average monthly best case

-27.55% Average annual worst case
47.38% Average annual best case

For the monte carlo simulation we had:

df_mc.mean()[0]
0.7945767826854163

For the trained agent we have:

optimized_avg_monthly_return = max(rewards2["mean"])/n_months
print(f"{optimized_avg_monthly_return:5.4f} optimized average monthly return")
0.9740 optimized average monthly return

This means the improvement brought about by the trained agent is 0.1794% per month:

print(f'improvement over random case: {optimized_avg_monthly_return - df_mc.mean()[0]:5.4f}% per month')
improvement over random case: 0.1794% per month

However, this is still far from the best case of 3.95% per month.

Overall, the contextual bandit performed well considering that it only used inflation for the context of its decisions (state of the environment), and could only take actions once a month.

Restore trained agent from a checkpoint

To avoid having to train the agent each time, the train artifacts can be restored from a checkpoint as follows:

# hide
# https://github.com/ray-project/ray/issues/9123
trainer = MarketLinTSTrainer(config=market_config)
trainer
/usr/local/lib/python3.7/dist-packages/gym/logger.py:30: UserWarning: WARN: Box bound precision lowered by casting to float32
  warnings.warn(colorize('%s: %s'%('WARN', msg % args), 'yellow'))
2021-12-07 20:34:07,772 WARNING util.py:57 -- Install gputil for GPU system monitoring.
MarketBandit: min_inflation: -100.0, max_inflation: 100.0, min_ppi: -250.0, max_ppi: 250.0, tickers: ['FBCVX', 'FCPGX', 'FDSVX', 'VBILX', '^GSPC'], data file: /content/gdrive/My Drive/RLlib/MAB-data.csv (config: {})
MarketLinTSTrainer
checkpoint_path
'/content/gdrive/My Drive/RLlib/RLlib-MAB-Trader_SAVED/MarketLinTSTrainer_2021-12-07_20-28-06/MarketLinTSTrainer_MarketBandit_2f4b3_00002_2_2021-12-07_20-28-21/checkpoint_000200/checkpoint-200'
trainer.restore(checkpoint_path=checkpoint_path)
2021-12-07 20:34:11,282 INFO trainable.py:468 -- Restored on 172.28.0.2 from checkpoint: /content/gdrive/My Drive/RLlib/RLlib-MAB-Trader_SAVED/MarketLinTSTrainer_2021-12-07_20-28-06/MarketLinTSTrainer_MarketBandit_2f4b3_00002_2_2021-12-07_20-28-21/checkpoint_000200/checkpoint-200
2021-12-07 20:34:11,285 INFO trainable.py:475 -- Current state after restoring: {'_iteration': 200, '_timesteps_total': 0, '_time_total': 83.15605854988098, '_episodes_total': 99}

Access the model, to review the distribution of arm weights

import pprint
model = trainer.get_policy().model
pprint.pprint(model.variables())
[Parameter containing:
tensor([[19655.3984]]),
 Parameter containing:
tensor([5930.8672]),
 Parameter containing:
tensor([[5.0877e-05]]),
 Parameter containing:
tensor([0.3017]),
 Parameter containing:
tensor([[24172.1680]]),
 Parameter containing:
tensor([11054.0928]),
 Parameter containing:
tensor([[4.1370e-05]]),
 Parameter containing:
tensor([0.4573]),
 Parameter containing:
tensor([[25337.4844]]),
 Parameter containing:
tensor([12553.6074]),
 Parameter containing:
tensor([[3.9467e-05]]),
 Parameter containing:
tensor([0.4955]),
 Parameter containing:
tensor([[16308.4043]]),
 Parameter containing:
tensor([3098.0303]),
 Parameter containing:
tensor([[6.1318e-05]]),
 Parameter containing:
tensor([0.1900])]
pprint.pprint(model.value_function())
tensor([[0., 0., 0., 0.],
        [0., 0., 0., 0.],
        [0., 0., 0., 0.],
        [0., 0., 0., 0.],
        [0., 0., 0., 0.],
        [0., 0., 0., 0.],
        [0., 0., 0., 0.],
        [0., 0., 0., 0.],
        [0., 0., 0., 0.],
        [0., 0., 0., 0.],
        [0., 0., 0., 0.],
        [0., 0., 0., 0.],
        [0., 0., 0., 0.],
        [0., 0., 0., 0.],
        [0., 0., 0., 0.],
        [0., 0., 0., 0.],
        [0., 0., 0., 0.],
        [0., 0., 0., 0.],
        [0., 0., 0., 0.],
        [0., 0., 0., 0.],
        [0., 0., 0., 0.],
        [0., 0., 0., 0.],
        [0., 0., 0., 0.],
        [0., 0., 0., 0.],
        [0., 0., 0., 0.],
        [0., 0., 0., 0.],
        [0., 0., 0., 0.],
        [0., 0., 0., 0.],
        [0., 0., 0., 0.],
        [0., 0., 0., 0.],
        [0., 0., 0., 0.],
        [0., 0., 0., 0.]])
# hide
# print(model.base_model.summary())
# model.arms.
means = [model.arms[i].theta.numpy() for i in range(3)]
means
[array([0.3017424], dtype=float32),
 array([0.45730665], dtype=float32),
 array([0.49545595], dtype=float32)]
covs = [model.arms[i].covariance.numpy() for i in range(3)]
covs
[array([[5.087661e-05]], dtype=float32),
 array([[4.1369894e-05]], dtype=float32),
 array([[3.9467217e-05]], dtype=float32)]
means, covs, model.arms[0].theta.numpy()
([array([0.3017424], dtype=float32),
  array([0.45730665], dtype=float32),
  array([0.49545595], dtype=float32)],
 [array([[5.087661e-05]], dtype=float32),
  array([[4.1369894e-05]], dtype=float32),
  array([[3.9467217e-05]], dtype=float32)],
 array([0.3017424], dtype=float32))

Final evaluation

bandit = MarketBandit()
episode_cumulative_reward = 0
episode_rewards = []
done = False
obs = bandit.reset()
while not done:
  action = trainer.compute_action(obs)
  obs, reward, done, info = bandit.step(action)
  episode_cumulative_reward += reward
  episode_rewards.append(episode_cumulative_reward)
  # print(obs, reward, done, info)
MarketBandit: min_inflation: -100.0, max_inflation: 100.0, min_ppi: -250.0, max_ppi: 250.0, tickers: ['FBCVX', 'FCPGX', 'FDSVX', 'VBILX', '^GSPC'], data file: /content/gdrive/My Drive/RLlib/MAB-data.csv (config: {})
/usr/local/lib/python3.7/dist-packages/gym/logger.py:30: UserWarning: WARN: Box bound precision lowered by casting to float32
  warnings.warn(colorize('%s: %s'%('WARN', msg % args), 'yellow'))
df['^GSPC'].cumsum()
0       -2.529047
1       -0.638712
2       -2.550478
3       -4.561336
4       -1.566131
          ...    
197    144.820669
198    147.095475
199    149.994516
200    145.237600
201    152.151983
Name: ^GSPC, Length: 202, dtype: float64
df_mc.loc[0:201, 'reward'].cumsum()
0       -4.813760
1       -5.723946
2       -6.780973
3      -13.985082
4      -11.014791
          ...    
197    110.392133
198    109.402571
199    104.464508
200    100.201109
201     95.387349
Name: reward, Length: 202, dtype: float64
min_max['min'].cumsum()
0       -4.813760
1       -5.723946
2       -8.441847
3      -15.645956
4      -14.200573
          ...    
197   -440.837905
198   -441.827467
199   -446.765530
200   -463.113897
201   -463.790798
Name: min, Length: 202, dtype: float64

The following chart shows performance in the wider setting of worst case and best case performances:

fig,axs = plt.subplots(figsize=(14,18))
axs.set_xlabel('Months', fontsize=20)
axs.set_ylabel('Cumulative Reward (%)', fontsize=20)
axs.set_title(f'MAB Agent over episode of 202 months ({202/12:2.0f} years)', fontsize=24)
axs.plot(episode_rewards, color='r', label='MAB Investment Agent')
axs.plot(df['^GSPC'].cumsum(), color='k', label='S&P500')
axs.plot(df_mc.loc[0:201, 'reward'].cumsum(), color='blue', label='Monte Carlo')
axs.plot(min_max['min'].cumsum(), color='k', label='Worst case', linestyle='-.')
axs.plot(min_max['max'].cumsum(), color='k', label='Best case', linestyle='--')
# axs.xaxis.set_major_locator(plt.AutoLocator())
axs.legend(fontsize=20);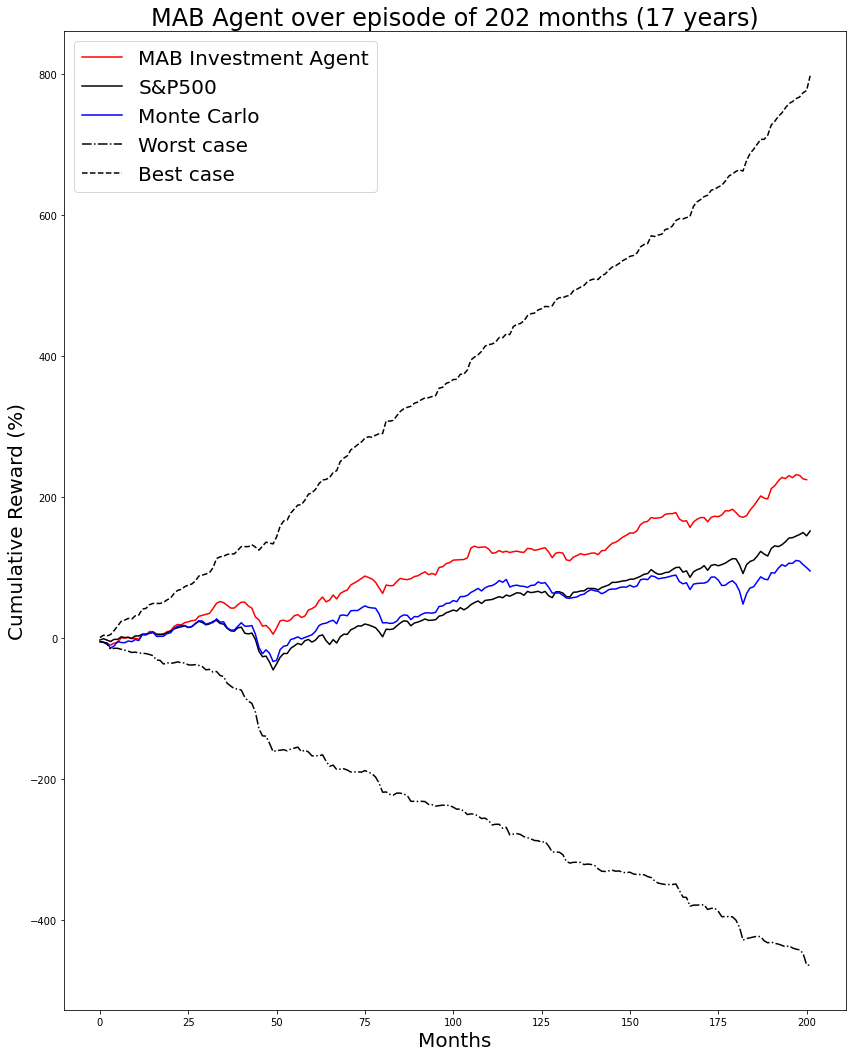

The next chart shows the performance of the trained agent against the S&P500:

fig,axs = plt.subplots(figsize=(14,10))
axs.set_xlabel('Months', fontsize=20)
axs.set_ylabel('Cumulative Reward (%)', fontsize=20)
axs.set_title(f'MAB Agent vs S&P500', fontsize=24)
axs.plot(episode_rewards, color='r', label='MAB Investment Agent')
axs.plot(df['^GSPC'].cumsum(), color='k', label='S&P500')
# axs.plot(df_mc.loc[0:201, 'reward'].cumsum(), color='blue', label='Monte Carlo')
# axs.plot(min_max['min'].cumsum(), color='k', label='Worst case', linestyle='-.')
# axs.plot(min_max['max'].cumsum(), color='k', label='Best case', linestyle='--')
# axs.xaxis.set_major_locator(plt.AutoLocator())
axs.legend(fontsize=20);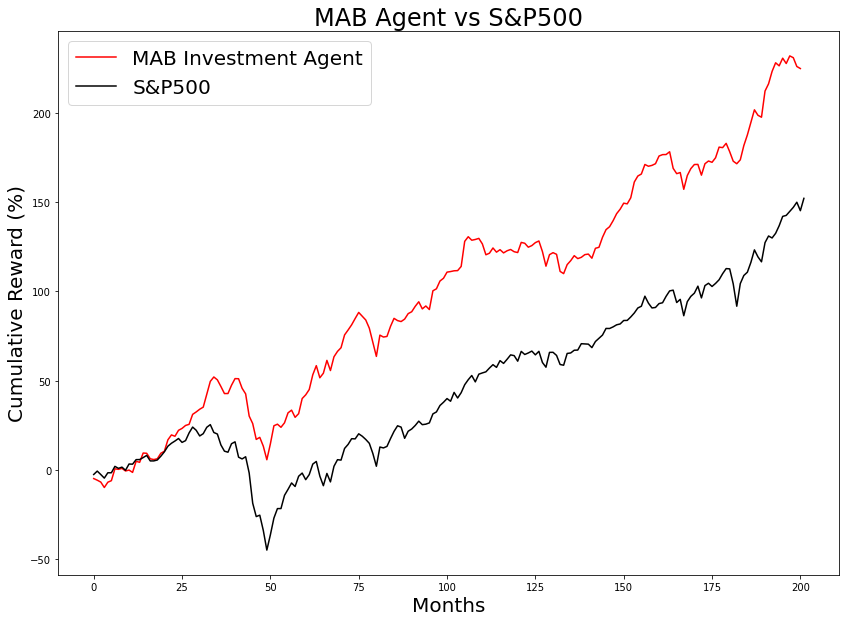

Finally, here is a summary of all the pertinent performances:

print('------- PERFORMANCE OF MAB AGENT -------')
print(f"Avg Monthly return: {episode_cumulative_reward/n_months:1.3f}%")
print(f"Avg Annual return: {12*episode_cumulative_reward/n_months:1.3f}%")
------- PERFORMANCE OF MAB AGENT -------
Avg Monthly return: 1.113%
Avg Annual return: 13.358%
print('------- PERFORMANCE OF S&P500 -------')
print(f"Avg Monthly return: {df['^GSPC'].cumsum().values[-1]/n_months:1.3f}%")
print(f"Avg Annual return: {12*df['^GSPC'].cumsum().values[-1]/n_months:1.3f}%")
------- PERFORMANCE OF S&P500 -------
Avg Monthly return: 0.753%
Avg Annual return: 9.039%
print('------- PERFORMANCE OF MONTE CARLO -------')
print(f"Avg Monthly return: {df_mc.loc[0:201, 'reward'].cumsum().values[-1]/n_months:1.3f}%")
print(f"Avg Annual return: {12*df_mc.loc[0:201, 'reward'].cumsum().values[-1]/n_months:1.3f}%")
------- PERFORMANCE OF MONTE CARLO -------
Avg Monthly return: 0.472%
Avg Annual return: 5.667%
print('------- PERFORMANCE OF WORST CASE -------')
print(f"Avg Monthly return: {min_max['min'].cumsum().values[-1]/n_months:1.3f}%")
print(f"Avg Annual return: {12*min_max['min'].cumsum().values[-1]/n_months:1.3f}%")
------- PERFORMANCE OF WORST CASE -------
Avg Monthly return: -2.296%
Avg Annual return: -27.552%
print('------- PERFORMANCE OF BEST CASE -------')
print(f"Avg Monthly return: {min_max['max'].cumsum().values[-1]/n_months:1.3f}%")
print(f"Avg Annual return: {12*min_max['max'].cumsum().values[-1]/n_months:1.3f}%")
------- PERFORMANCE OF BEST CASE -------
Avg Monthly return: 3.949%
Avg Annual return: 47.383%
ray.shutdown()

Disclaimer

This content is only meant for research purposes and is not meant to be used in any form of trading. Past performance is no guarantee of future results. If you suffer losses from making use of this content, directly or indirectly, you are the sole person responsible for the losses. The author will not be held responsible in any way.