Dealership Inventory Management using the Powell Unified Framework (Part 4)

Using Sequential Decision Analytics to find ongoing optimal decisions

Automotive Industry
Inventory Management
Powell Unified Framework
Reinforcement Learning
Python
Author

Kobus Esterhuysen

Published

November 7, 2022

0 INTRODUCTION

In part 3 we added stockout costs as well as holding costs to complicate Mr. Optimal’s task of managing the number of Elantras and Sonatas on his dealership space of 57 lots. So far, he has chosen to partition the 57 lots between the models as 40 for Elantras and 17 for Sonatas. These parameters were indicated by \(R^{maxELA}\) and \(R^{maxSON}\). The question in this project is whether this partitioning could have been done in a more optimal way. We will now add two more learnable parameters, \(\theta^{maxELA}\) and \(\theta^{maxSON}\). This will allow us to have an order-up-to policy. Whenever the inventory level of say the Elantras falls below \(\theta^{buy}_{ELA}\), Mr. Optimal will place an order - however not up to \(R^{maxELA}=40\) anymore, but up to \(R^{maxELA}=\theta^{max}_{ELA}\). The same rule will apply for the Sonatas. In total we will have four parameters to learn which leads to the parameter vector: \[((\theta^{buy}_{ELA}, \theta^{buy}_{SON}), (\theta^{max}_{ELA}, \theta^{max}_{SON}))\]

We will also make the code more generic so that it can be scaled up in the future without too much trouble. For example, instead of hardcoding variables, we often access them by traversing the entity names list eNames.

The overall structure of this project and report follows the traditional CRISP-DM format. However, instead of the CRISP-DM’S “4 Modeling” section, we inserted the “6 step modeling process” of Dr. Warren Powell in section 4 of this document. Dr Powell’s unified framework shows great promise for unifying the formalisms of at least a dozen different fields. Using his framework enables easier access to thinking patterns in these other fields that might be beneficial and informative to the sequential decision problem at hand. Traditionally, this kind of problem would be approached from the reinforcement learning perspective. However, using Dr. Powell’s wider and more comprehensive perspective almost certainly provides additional value.

Here is information on Dr. Powell’s perspective on Sequential Decision Analytics.

In order to make a strong mapping between the code in this notebook and the mathematics in the Powell Unified Framework (PUF), we follow the following convention for naming Python identifier names:

  • Superscripts
    • variable names have a double underscore to indicate a superscript
    • \(X^{\pi}\): has code X__pi, is read X pi
  • Subscripts
    • variable names have a single underscore to indicate a subscript
    • \(S_t\): has code S_t, is read ‘S at t’
    • \(M^{Spend}_t\) has code M__Spend_t which is read: “MSpend at t”
  • Arguments
    • collection variable names may have argument information added
    • \(X^{\pi}(S_t)\): has code X__piIS_tI, is read ‘X pi in S at t’
    • the surrounding I’s are used to imitate the parentheses around the argument
  • Next time/iteration
    • variable names that indicate one step in the future are quite common
    • \(R_{t+1}\): has code R_tt1, is read ‘R at t+1’
    • \(R^{n+1}\): has code R__nt1, is read ‘R at n+1’
  • Rewards
    • State-independent terminal reward and cumulative reward
      • \(F\): has code F for terminal reward
      • \(\sum_{n}F\): has code cumF for cumulative reward
    • State-dependent terminal reward and cumulative reward
      • \(C\): has code C for terminal reward
      • \(\sum_{t}C\): has code cumC for cumulative reward
  • Vectors where components use different names
    • \(S_t(R_t, p_t)\): has code S_t.R_t and S_t.p_t, is read ‘S at t in R at t, and, S at t in p at t’
    • the code implementation is by means of a named tuple
      • self.State = namedtuple('State', SVarNames) for the ‘class’ of the vector
      • self.S_t for the ‘instance’ of the vector
  • Vectors where components reuse names
    • \(x_t(x_{t,GB}, x_{t,BL})\): has code x_t.x_t_GB and x_t.x_t_BL, is read ‘x at t in x at t for GB, and, x at t in x at t for BL’
    • the code implementation is by means of a named tuple
      • self.Decision = namedtuple('Decision', xVarNames) for the ‘class’ of the vector
      • self.x_t for the ‘instance’ of the vector
  • Use of mixed-case variable names
    • to reduce confusion, sometimes the use of mixed-case variable names are preferred (even though it is not a best practice in the Python community), reserving the use of underscores and double underscores for math-related variables

1 BUSINESS UNDERSTANDING

Inventory management is a critical component of any business, whether it be a small retail store or a multinational corporation. At its core, inventory management is the process of tracking and controlling a company’s inventory, from raw materials to finished products. Proper inventory management is important for several reasons.

First and foremost, inventory management helps businesses avoid stock overages and underages (overstocks and stockouts). By tracking inventory levels and forecasting demand, businesses can ensure that they always have the right amount of product on hand to meet customer needs without overbuying and tying up capital in excess inventory. This helps businesses maintain a healthy cash flow and avoid costly stockouts that can result in lost sales and dissatisfied customers.

In addition, effective inventory management can help businesses streamline their operations and improve their overall efficiency. By reducing excess inventory and optimizing order quantities and lead times, businesses can minimize waste and improve their supply chain management. This can lead to cost savings, improved profitability, and increased customer satisfaction.

Finally, inventory management is critical for businesses that need to comply with regulatory requirements, such as those in the pharmaceutical or food industries. Proper inventory tracking and documentation can help businesses meet these requirements and avoid costly fines and penalties.

Overall, inventory management is an essential function for any business that wants to operate efficiently, meet customer demand, and maximize profitability. Effective inventory management requires careful planning, accurate data, and the right tools and processes to ensure that businesses always have the right amount of product on hand, at the right time, and at the right cost.

In this project the client had a need to be convinced of the benefits of formal optimized sequential decision making. This was provided in the form of a series of POCs.

2 DATA UNDERSTANDING

Based on recent market research, the demand may be modeled by two Poisson distributions with means: \[ \begin{aligned} \mu^{ELA} &= 19 \\ \mu^{SON} &= 8 \end{aligned} \]

We will simulate the inventory demand for Elantras, \(D^{ELA}\), by: \[ D^{ELA}_{t+1} \sim Pois(\mu^{ELA}) \]

Similarly,

the inventory demand for Sonatas, \(D^{SON}\), is given by: \[ D^{SON}_{t+1} \sim Pois(\mu^{SON}) \]

The order window is 1 month and these simulations are for the monthly demands.

# !pip install multidispatch
# import pdb
from collections import namedtuple, defaultdict
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from copy import copy
import time
from scipy.ndimage.interpolation import shift
import pickle
from bisect import bisect
import math
from pprint import pprint
import matplotlib as mpl
from certifi.core import where
pd.options.display.float_format = '{:,.4f}'.format
pd.set_option('display.max_columns', None)
pd.set_option('display.max_rows', None)
pd.set_option('display.max_colwidth', None)
! python --version
Python 3.10.11
DeprecationWarning: Please use `shift` from the `scipy.ndimage` namespace, the `scipy.ndimage.interpolation` namespace is deprecated.
  from scipy.ndimage.interpolation import shift

The parameters of the inventory system under management (SUM) are:

SNames = ['R_t', 'D_t']
xNames = ['x_t']
eNames = ['ELA', 'SON']
piNames = ['X__BuyBelow']

T__sim = 60 #50 #100
muD = {'ELA': 19, 'SON': 8}
eventTimeD = {'ELA': None, 'SON': None}
muDeltaD = {'ELA': None, 'SON': None}

p__buy = {'ELA': 19_300, 'SON': 22_100} #dollars
p__sell = {'ELA': 23_470, 'SON': 27_250} #dollars

# R__maxELA = 40 #spaces #is now learned
# R__maxSON = 17 #spaces #is now learned

c__interest = 0.05/12

c__upkeep = {'ELA': 28.43, 'SON': 34.72} #dollars per item
class DemandSimulator():
    def __init__(self, 
            T__sim, 
            muD, 
            eventTimeD,
            muDeltaD):
        self.time = 0
        self.T__sim = T__sim
        self.muD = muD
        self.eventTimeD = eventTimeD
        self.muDeltaD = muDeltaD    

    def simulate(self):
        if self.time > T__sim - 1:
            self.time = 0
        D_tt1 = {}
        for e in eNames:
            if self.eventTimeD[e] and self.time > self.eventTimeD[e]: #event for entity
                D_tt1[e] = self.muDeltaD[e] + np.random.poisson(self.muD[e]) #after event
            else:
                D_tt1[e] = np.random.poisson(self.muD[e])
        self.time += 1
        return {e: max(0, D_tt1[e]) for e in eNames} #always positive
dem_sim = DemandSimulator(
    T__sim=T__sim, 
    muD=muD,
    eventTimeD=eventTimeD,
    muDeltaD=muDeltaD)

DemandData = []
for i in range(T__sim):
  d_e = list(dem_sim.simulate().values())
  DemandData.append(d_e)
labels = [f'{e}_demand' for e in eNames]
df = pd.DataFrame.from_records(data=DemandData, columns=labels); df[:10]
ELA_demand SON_demand
0 12 10
1 19 7
2 18 10
3 18 9
4 15 11
5 27 3
6 10 4
7 20 10
8 22 11
9 19 4 
import random
def plot_output(df1, df2):
  n_charts = len(eNames)
  ylabelsize = 16
  mpl.rcParams['lines.linewidth'] = 1.2
  default_colors = plt.rcParams['axes.prop_cycle'].by_key()['color']
  fig, axs = plt.subplots(n_charts, sharex=True)
  fig.set_figwidth(13); fig.set_figheight(9)
  fig.suptitle('Demand Simulation', fontsize=20)

  for i,e in enumerate(eNames):
    axs[i].set_title(f'Demanded {e}')
    axs[i].set_ylim(auto=True); axs[i].spines['top'].set_visible(False); axs[i].spines['right'].set_visible(True); axs[i].spines['bottom'].set_visible(False)
    axs[i].step(df1[f'{e}_demand'], random.choice(default_colors))
    axs[i].axhline(y=dem_sim.muD[e], color='k', linestyle=':')

  axs[i].set_xlabel('$t\ \mathrm{[monthly\ order\ windows]}$', rotation=0, ha='center', va='center', fontweight='bold', size=ylabelsize)
plot_output(df, None)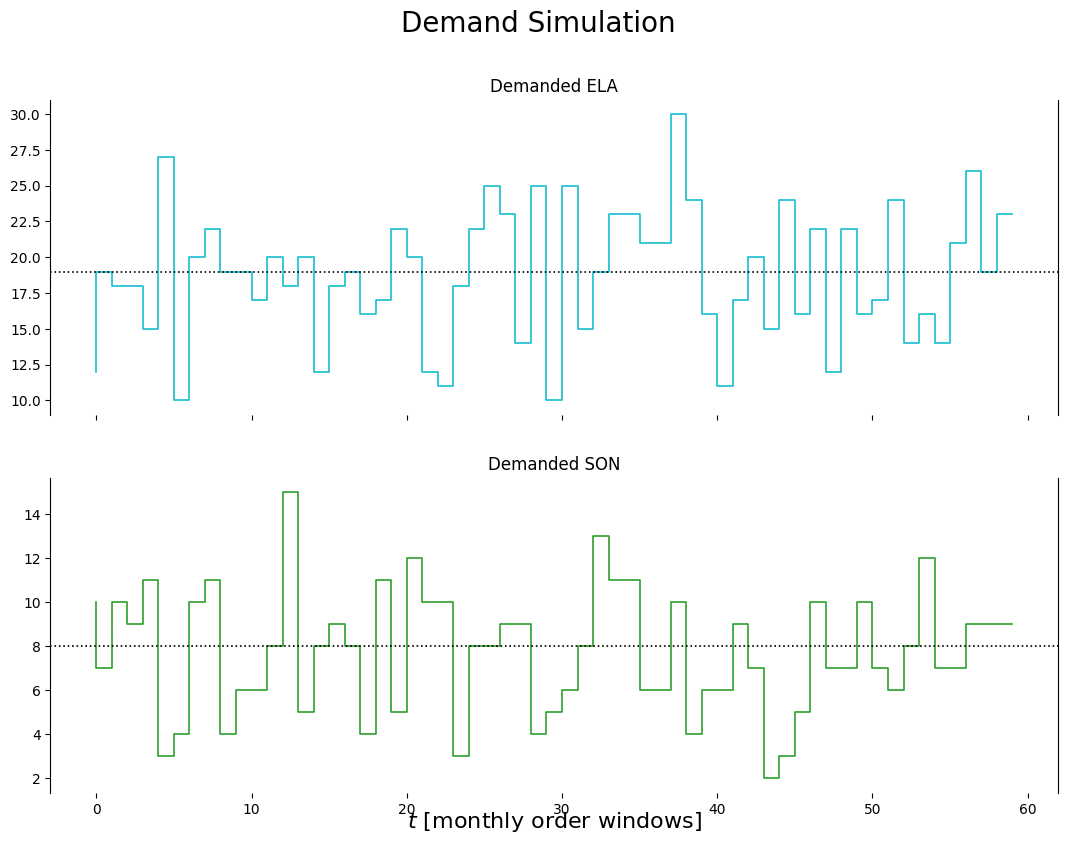

seed = 189654913
file = 'Parameters.xlsx'
# NOTE:
# R__max: maximum number of inventory units
# R_0:    initial number of inventory units
parDf = pd.read_excel(f'{base_dir}/{file}', sheet_name='ParamsModel', index_col=0); print(f'{parDf}')
parDict = parDf.T.to_dict('list') #.
params = {key:v for key, value in parDict.items() for v in value}
params['seed'] = seed
params['T'] = min(params['T'], 192); print(f'{params=}')
                    0
Index                
Algorithm  GridSearch
T                 195
eta                 1
R__max             57
R_0                 0
params={'Algorithm': 'GridSearch', 'T': 192, 'eta': 1, 'R__max': 57, 'R_0': 0, 'seed': 189654913}
parDf = pd.read_excel(f'{base_dir}/{file}', sheet_name='GridSearch', index_col=0); print(parDf)
parDict = parDf.T.to_dict('list')
paramsPolicy = {key:v for key, value in parDict.items() for v in value}; print(f'{paramsPolicy=}')
params.update(paramsPolicy); pprint(f'{params=}')
                  0
Index              
theta_sell_min   10
theta_sell_max  100
theta_buy_min    10
theta_buy_max   100
theta_inc         1
paramsPolicy={'theta_sell_min': 10, 'theta_sell_max': 100, 'theta_buy_min': 10, 'theta_buy_max': 100, 'theta_inc': 1}
("params={'Algorithm': 'GridSearch', 'T': 192, 'eta': 1, 'R__max': 57, 'R_0': "
 "0, 'seed': 189654913, 'theta_sell_min': 10, 'theta_sell_max': 100, "
 "'theta_buy_min': 10, 'theta_buy_max': 100, 'theta_inc': 1}")
pprint(f"{params=}")
("params={'Algorithm': 'GridSearch', 'T': 192, 'eta': 1, 'R__max': 57, 'R_0': "
 "0, 'seed': 189654913, 'theta_sell_min': 10, 'theta_sell_max': 100, "
 "'theta_buy_min': 10, 'theta_buy_max': 100, 'theta_inc': 1}")

3 DATA PREPARATION

We will use the data provided by the simulator directly. There is no need to perform additional data preparation.

4 MODELING

4.1 Narrative

As pointed out in the introduction, this fourth project in the Inventory Series expands the problem in part 3 to have four parameters:

\[((\theta^{buy}_{ELA}, \theta^{buy}_{SON}), (\theta^{max}_{ELA}, \theta^{max}_{SON}))\]

To remind the reader, we have the following setting: Mr. Optimal is an inventory manager for the largest dealership in a big city. He is responsible to manage the inventory levels of the two mentioned Hyundai models. He has a maximum number of lot spaces assigned to him (which is 57). So far, Mr. Optimal decided to reserve a maximum of 40 spaces for the Elantras. The remaining 17 spaces will be used for Sonata. In this project he will instead rely on the two learned values for the maximum number of spaces for the two models. He has a choice to strive to always keep these spaces occupied by new cars. This way he is unlikely to run out of stock and lose a sale due to that. However, capital is tied up by the unsold inventory in his lot space.

At the other extreme, he may choose to work on a just-in-time principle: Each time a potential customer expresses interest in a model, the customer will have to wait until he obtains a new car from the supplier. Of course, he will likely lose the sale, but the upside is that no capital is tied up in his inventory.

It seems intuitive that the optimal levels of inventory will be somewhere between these extremes. The challenge is to find that optimal levels. For now, we will assume that the buy and sell prices will remain constant. The only random variables will be the demands for these models. Another assumption is that ordered inventory will arrive immediately.

Unsatisfied demands are lost, i.e. there will be no ability to backlog unsatisfied demands. However, a stockout cost is incurred when demand is unsatisfied. Moreover, existing inventory brings about a holding cost for each item. The latter cost is usually made up of lost interest on cash used to buy the item as well as upkeep cost. Under upkeep we could think of making sure batteries are kept in a charged state, fuel associated with drive arounds to showcase a vehicle, as well as costs associated with keeping the vehicles clean and groomed.

4.2 Core Elements

This section attempts to answer three important questions: - What metrics are we going to track? - What decisions do we intend to make? - What are the sources of uncertainty?

For this problem, the only metric we are interested in is the amount of profit we make after each decision window. A single type of decision needs to be made at the start of each window - how many new cars to order of each model. The only source of uncertainty are the levels of demand for the models.

4.3 Mathematical Model | SUM Design

A Python class is used to implement the model for the SUM (System Under Management):

class InventoryStorageModel():
    def __init__(
        self, SNames, xNames, eNames, params, exogParams, possibleDecisions,
        p__buy, p__sell, W_fn=None, S__M_fn=None, C_fn=None):
        ...
        ...

4.3.1 State variables

The state variables represent what we need to know. - \(R_t = (R_{te})_{e \in \cal E}\) where \(\cal{E} = \mathrm{\{ELA, SON\}}\) - the inventory on hand at time \(t\) before we make a new ordering decision, and before we have satisfied any demands arising in time interval \(t\) - measured in inventory units - \(D_t = (D_{te})_{e \in \cal E}\) where \(\cal{E} = \mathrm{\{ELA, SON\}}\) - the demand - measured in inventory units

The state is:

  • \(S_t = (R_t, D_t) = ((R_{te})_{e \in \cal E}, (D_{te})_{e \in \cal E})\)

The state variables are represented by the following variables in the InventoryStorageModel class:

self.SNames = SNames
self.State = namedtuple('State', SNames) # 'class'
self.S_t = self.build_state(self.S_0) # 'instance'

where

SNames = ['R_t', 'D_t']

4.3.2 Decision variables

The decision variables represent what we control.

  • \(x_t = (x_{te})_{e\in \cal X}\) where \(\cal{X} = \mathrm{\{ELA, SON\}} = \cal E\)
    • number of Elantras and Sonatas ordered (\(x_t\ge0\)) where \(x_t\) is a positive integer
  • Constraints
    • \(x_{t,ELA} \le (R^{maxELA} - R_{t,ELA})\) where \(R^{maxELA} = \theta^{max}_{ELA}\), a learned parameter
    • \(x_{t,SON} \le (R^{maxSON} - R_{t,SON})\) where \(R^{maxSON} = \theta^{max}_{SON}\), a learned parameter
    • \(R^{max}\) is the number of lot units (i.e. parking spaces) assigned to Mr. Optimal
    • \(R^{max} = R^{maxELA} + R^{maxSON} = 57\)
  • Decisions are made with a policy (TBD below):
    • \(X^{\pi}(S_t)\)

The decision variables are represented by the following variables in the InventoryStorageModel class:

self.Decision = namedtuple('Decision', xNames) # 'class'

where

xNames = ['x_t']

4.3.3 Exogenous information variables

The exogenous information variables represent what we did not know (when we made a decision). These are the variables that we cannot control directly. The information in these variables become available after we make the decision \(x_t\).

We assume that any unsatisfied demand is lost. Additionally, we assume that the demand in each time period is revealed, so that we have:

\[ W_{t+1} = \hat{D}_{t+1}=D_{t+1} \]

The exogenous information is obtained by a call to

DemandSimulator.simulate(...)

The latest exogenous information can be accessed by calling the following method from class InventoryStorageModel():

def W_fn(self, t):
    W_tt1_ELA, W_tt1_SON = dem_sim.simulate()
    W_ttl = {'ELA': W_tt1_ELA, 'SON': W_tt1_SON}
    return W_ttl

4.3.4 Transition function

The transition function describe how the state variables evolve over time. Because we currently have two state variables in the state, \(S_t=(R_t,D_t)\), we have the equations:

\[ \begin{aligned} R_{t+1} &= (R_{t,ELA} - \mathrm{min}\{R_{t,ELA},D_{t,ELA}\}+x_{t,ELA}, R_{t,SON} - \mathrm{min}\{R_{t,SON},D_{t,SON}\}+x_{t,SON}) \quad (Eq. 1) \\ D_{t+1} &= (\hat{D}_{t+1,ELA}, \hat{D}_{t+1,SON}) \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad (Eq. 2) \end{aligned} \]

Collectively, they represent the general transition function:

\[ S_{t+1} = S^M(S_t,X^{\pi}(S_t)) \] The transition function is implemented by the following method in class InventoryStorageModel():

def S__M_fn(self, x_t, Dhat_tt1):
    R_tt1 = {e: max( 0, self.S_t.R_t[e] - min(self.S_t.R_t[e], self.S_t.D_t[e]) + x_t.x_t[e] ) for e in eNames} #max to keep >0
    D_tt1 = {e: Dhat_tt1[e] for e in eNames}
    S_tt1 = self.build_state({
        'R_t': {e: R_tt1[e] for e in eNames}, 
        'D_t': {e: D_tt1[e] for e in eNames}
    })
    return S_tt1

4.3.5 Objective function

The objective function captures the performance metrics of the solution to the problem.

First, let us state the stockout and holding costs:

\[ \begin{align} c^{soutELA} &= p^{sellELA}\max\{D_{t,ELA} - R_{t,ELA}, 0 \} \\ c^{soutSON} &= p^{sellSON}\max\{D_{t,SON} - R_{t,SON}, 0 \} \\ c^{holdELA} &= c^{interest}p^{buyELA} + c^{upkeepELA} \\ c^{holdSON} &= c^{interest}p^{buySON} + c^{upkeepSON} \end{align} \] where the first two equations represent the opportunity cost of unsatisfied demand. The last two equations represent the interest and upkeep costs for each item over each order window. Each of these costs will have to be subtracted from the contribution, \(C\).

We can write the state-dependant reward (also called contribution) based on what we will receive between \(t-1\) and \(t\) (i.e. looking backward relative to \((S_t,x_t)\)):

\[ \begin{align} C(S_t,x_t) = p^{sellELA}\min\{R_{t,ELA}, D_{t,ELA}\} - p^{buyELA}x_{t,ELA} - c^{soutELA} - c^{holdELA} \\ + p^{sellSON}\min\{R_{t,SON}, D_{t,SON}\} - p^{buySON}x_{t,SON} - c^{soutSON} - c^{holdSON} \end{align} \] This is a deterministic expression.

Alternatively, we can write the state-dependant reward based on what we will receive between \(t\) and \(t+1\) (i.e. looking forward relative to \((S_t,x_t)\)):

\[ \begin{aligned} C(S_t,x_t,\hat{D}_{t+1}) & = p^{sellELA}\min\{R_{t+1,ELA},D_{t+1,ELA}\} - p^{buyELA}x_{t,ELA} - c^{soutELA} - c^{holdELA} + p^{sellSON}\min\{R_{t+1,SON},D_{t+1,SON}\} - p^{buySON}x_{t,SON} - c^{soutSON} - c^{holdSON} \\ & = p^{sellELA}\mathrm{min}\{(R_{t,ELA}-\mathrm{min}\{R_{t,ELA}, D_{t,ELA}\}+x_{t,ELA}), \hat{D}_{t+1,ELA}\} - p^{buyELA}x_{t,ELA} - c^{soutELA} - c^{holdELA} + p^{sellSON}\mathrm{min}\{(R_{t,SON}-\mathrm{min}\{R_{t,SON}, D_{t,SON}\}+x_{t,SON}), \hat{D}_{t+1,SON}\} - p^{buySON}x_{t,SON} - c^{soutSON} - c^{holdSON} \end{aligned} \]

because, from (Eq. 1) and (Eq. 2) above:

\[ \begin{aligned} R_{t+1} &= (R_{t,ELA} - \mathrm{min}\{R_{t,ELA},D_{t,ELA}\}+x_{t,ELA}, R_{t,ELA} - \mathrm{min}\{R_{t,ELA},D_{t,ELA}\}+x_{t,ELA}) \quad (Eq. 1) \\ D_{t+1} &= (\hat{D}_{t+1,ELA}, \hat{D}_{t+1,SON}) \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad (Eq. 2) \end{aligned} \]

This is a stochastic expression due to the dependence on the random variable \(\hat{D}_{t+1}\). It is random because it comes from a stochastic process but it is also in the future.

This second form leads to the objective function:

\[ \max_{\pi}\mathbb{E}\{\sum_{t=0}^{T}C(S_t,x_t,W_{t+1}) \} \]

The contribution (reward) function is implemented by the following method in class InventoryStorageModel:

def C_fn(self, x_t):
    Dhat_tt1 = dem_sim.simulate()        
    c__sout = {e: self.p__sell[e]*max(self.S_t.D_t[e] - self.S_t.R_t[e], 0) for e in eNames} #unmet demand
    c__hold = {e: c__interest*self.p__buy[e] + c__upkeep[e] for e in eNames} #interest & upkeep
    C = 0
    for e in eNames:
      C += self.p__sell[e]*min((self.S_t.R_t[e] - min(self.S_t.R_t[e], self.S_t.D_t[e]) + x_t.x_t[e]), Dhat_tt1[e]) \
        - self.p__buy[e]*x_t.x_t[e] - c__sout[e] - c__hold[e] 
    return C, Dhat_tt1 #pass along exog_info, else data is skipped/wasted

4.3.6 Implementation of SUM Model

Here is the complete implementation of the InventoryStorageModel class:

class InventoryStorageModel():
    def __init__(
        self, SNames, xNames, eNames, params, exogParams, possibleDecisions,
        p__buy, p__sell, W_fn=None, S__M_fn=None, C_fn=None):
        self.initArgs = params
        self.prng = np.random.RandomState(params['seed'])
        self.exogParams = exogParams
        self.S_0 = {
          'R_t': {e: params['R_0'][0] for e in eNames},
          'D_t': {e: 0 for e in eNames},
        }
        self.SNames = SNames
        self.xNames = xNames
        self.eNames = eNames
        self.possibleDecisions = possibleDecisions
        self.p__buy = p__buy
        self.p__sell = p__sell
        self.State = namedtuple('State', SNames) #. 'class'
        self.S_t = self.build_state(self.S_0) #. 'instance'
        self.Decision = namedtuple('Decision', xNames) #. 'class'
        self.cumC = 0.0 #. cumulative reward

    def reset(self):
        self.cumC = 0.0
        self.S_t = self.build_state(self.S_0)

    def build_state(self, info):
        return self.State(*[info[sn] for sn in self.SNames])

    def build_decision(self, info):
        return self.Decision(*[info[xn] for xn in self.xNames])

    def W_fn(self, t):
        W_tt1_ELA, W_tt1_SON = dem_sim.simulate()
        W_ttl = {'ELA': W_tt1_ELA, 'SON': W_tt1_SON}
        return W_ttl

    def S__M_fn(self, x_t, Dhat_tt1):
        R_tt1 = {e: max( 0, self.S_t.R_t[e] - min(self.S_t.R_t[e], self.S_t.D_t[e]) + x_t.x_t[e] ) for e in eNames} #max to keep >0
        D_tt1 = {e: Dhat_tt1[e] for e in eNames}
        S_tt1 = self.build_state({
            'R_t': {e: R_tt1[e] for e in eNames}, 
            'D_t': {e: D_tt1[e] for e in eNames}
        })
        return S_tt1

    # based on what we will receive between t and t+1 (i.e. looking *forward* relative to (S_t,x_t) #.
    # RLSO-Eq8.5
    def C_fn(self, x_t):
        Dhat_tt1 = dem_sim.simulate()        
        c__sout = {e: self.p__sell[e]*max(self.S_t.D_t[e] - self.S_t.R_t[e], 0) for e in eNames} #unmet demand
        c__hold = {e: c__interest*self.p__buy[e] + c__upkeep[e] for e in eNames} #interest & upkeep
        C = 0
        for e in eNames:
          C += self.p__sell[e]*min((self.S_t.R_t[e] - min(self.S_t.R_t[e], self.S_t.D_t[e]) + x_t.x_t[e]), Dhat_tt1[e]) \
            - self.p__buy[e]*x_t.x_t[e] - c__sout[e] - c__hold[e] 
        return C, Dhat_tt1 #pass along exog_info, else data is skipped/wasted

    def step(self, t, x_t):
        C, Dhat_tt1 = self.C_fn(x_t)
        self.cumC += C
        self.S_t = self.S__M_fn(x_t, Dhat_tt1)
        return (self.S_t, self.cumC, x_t) #. for plotting

4.4 Uncertainty Model

We will simulate the inventory demand vector \(D_{t+1} = (D_{t+1,ELA}, D_{t+1,SON})\) as described in section 2.

4.5 Policy Design

There are two main meta-classes of policy design. Each of these has two subclasses: - Policy Search - Policy Function Approximations (PFAs) - Cost Function Approximations (CFAs) - Lookahead - Value Function Approximations (VFAs) - Direct Lookaheads (DLAs)

In this project we will only use one approach: - A simple buy below parameterized policy (from the PFA class)

The buy below policy is implemented by the following method in class InventoryStoragePolicy():

def X__BuyBelow(self, t, S_t, theta, T): #theta is a vector
    info = {
        'x_t': {'ELA': 0, 'SON': 0}
    }
    if t >= T:
        print(f"ERROR: t={t} should not reach or exceed the max steps ({T})")
        return self.model.build_decision(info)
    theta__buy_ELA = theta[0]
    R__maxELA = theta[2]
    if S_t.R_t['ELA'] <= theta__buy_ELA: # BUY if R_t_ELA <= theta__buy_ELA
        info['x_t']['ELA'] = R__maxELA - S_t.R_t['ELA']
    theta__buy_SON = theta[1]
    R__maxSON = theta[3]
    if S_t.R_t['SON'] <= theta__buy_SON: # BUY if R_t_SON <= theta__buy_SON
        info['x_t']['SON'] = R__maxSON - S_t.R_t['SON']
    return self.model.build_decision(info)

4.5.1 Implementation of Policy Design

The InventoryStoragePolicy() class implements the policy design.

import random
# from multidispatch import dispatch
from certifi.core import where
class InventoryStoragePolicy():
    def __init__(self, model, piNames):
        self.model = model
        self.piNames = piNames
        self.Policy = namedtuple('Policy', piNames)

    def X__BuyBelow(self, t, S_t, theta, T): #theta is a vector
        info = {
            'x_t': {'ELA': 0, 'SON': 0}
        }
        if t >= T:
            print(f"ERROR: t={t} should not reach or exceed the max steps ({T})")
            return self.model.build_decision(info)
        theta__buy_ELA = theta[0]
        R__maxELA = theta[2]
        if S_t.R_t['ELA'] <= theta__buy_ELA: # BUY if R_t_ELA <= theta__buy_ELA
            info['x_t']['ELA'] = R__maxELA - S_t.R_t['ELA']
        theta__buy_SON = theta[1]
        R__maxSON = theta[3]
        if S_t.R_t['SON'] <= theta__buy_SON: # BUY if R_t_SON <= theta__buy_SON
            info['x_t']['SON'] = R__maxSON - S_t.R_t['SON']
        return self.model.build_decision(info)

    def run_policy(self, piInfo, piName, params):
        model_copy = copy(self.model)
        T = params['T']
        for t in range(T): #for each transition/step
            x_t = getattr(self, piName)(t, model_copy.S_t, piInfo, T) # piInfo is theta value
            _, _, _ = model_copy.step(t, x_t)
        cumC = model_copy.cumC        
        return cumC

    def perform_grid_search(self, params, thetas):
        tS = time.time()
        cumCI_theta_I = {}
        bestTheta = None
        i = 0; print(f'... printing every 100th theta ...')
        for theta in thetas:
            if i%100 == 0: print(f'=== {theta=} ===')
            cumC = self.run_policy(theta, "X__BuyBelow", params)
            cumCI_theta_I[theta] = cumC
            best_theta = max(cumCI_theta_I, key=cumCI_theta_I.get)
            # print(f"Finishing theta {theta} with cumC {cumC:,}. Best theta so far {best_theta}. Best cumC {cumCI_theta_I[best_theta]:,}")
            i += 1
        print(f"Finishing GridSearch in {time.time() - tS:.2f} secs")
        print(f"Best theta: {best_theta}. Best cumC: {cumCI_theta_I[best_theta]:,}")
        return cumCI_theta_I, best_theta

    def run_policy_sample_paths(self, T, L, theta, pi, record): #theta could be a vector
        FhatIomega__lI = []
        for l in range(1, L + 1): #for each sample-path
            model_copy = copy(self.model)
            record_l = [pi, theta, l]
            for t in range(T): #for each transition/step
                x_t = getattr(self, pi)(t, model_copy.S_t, theta, T)
                # _, _, _ = model_copy.step(t, x_t)
                S_t, cumC, x_t = model_copy.step(t, x_t)
                record_t = [t] + [S_t.R_t[e] for e in eNames] + [S_t.D_t[e] for e in eNames] + [cumC] + [x_t.x_t[e] for e in eNames]
                record.append(record_l + record_t)
            FhatIomega__lI.append(model_copy.cumC) # just above (SDAM-eq2.9); Fhat for this sample-path is in model_copy.cumC
        return FhatIomega__lI

    def perform_grid_search_sample_paths(self, T, L, thetas, pi):
        tS = time.time()
        Fhat_mean = None
        Fhat_var = None
        Fhat__meanI_th_I = defaultdict(float) #{}
        Fhat__stdvI_th_I = defaultdict(float) #{}
        num_thetas = len(thetas)
        record = []
        i = 0; print(f'... printing every 20th theta if considered ...')
        for theta in thetas:
            # theta__buy_ELA < theta_max_ELA
            # theta__buy_SON < theta_max_SON
            # theta_max_ELA + theta_max_SON == 57
            if( (theta[0] < theta[2]) and \
                (theta[1] < theta[3]) and \
                (theta[2] + theta[3] == 57) ):
                if i%20 == 0: print(f'=== ({i:,} / {num_thetas:,}), {theta=} ===')      
                
                FhatIomega__lI = self.run_policy_sample_paths(
                    T, L, theta, pi, record)
                
                Fhat_mean = np.array(FhatIomega__lI).mean() #. (SDAM-eq2.9); call Fbar in future
                Fhat_var = np.sum(np.square(np.array(FhatIomega__lI) - Fhat_mean))/(L - 1)
                Fhat__meanI_th_I[theta] = Fhat_mean
                Fhat__stdvI_th_I[theta]= np.sqrt(Fhat_var/L)
                best_theta = max(Fhat__meanI_th_I, key=Fhat__meanI_th_I.get)
                # print(f"Finishing theta {theta} with cumC {Fhat__meanI_th_I[best_theta]:,}. Best theta so far {best_theta}. Best cumC {Fhat__meanI_th_I[best_theta]:,}")
            i += 1
        print(f"Finishing GridSearch in {time.time() - tS:.2f} secs")
        print(f"Best theta: {best_theta}. Best cumC: {Fhat__meanI_th_I[best_theta]:,}")
        return Fhat__meanI_th_I, Fhat__stdvI_th_I, best_theta, record

    # dispatch {prepend @}
    # def grid_search_theta_values(self, thetas0): #. using vectors reduces loops in perform_grid_search_sample_paths()
    #     thetas = [(th0,) for th0 in thetas0]
    #     return thetas

    # dispatch {prepend @}
    # def grid_search_theta_values(self, thetas0, thetas1): #. using vectors reduces loops in perform_grid_search_sample_paths()
    #     thetas = [(th0, th1) for th0 in thetas0 for th1 in thetas1]
    #     return thetas

    # dispatch {prepend @}
    # def grid_search_theta_values(self, thetas0, thetas1, thetas2): #. using vectors reduces loops in perform_grid_search_sample_paths()
    #     thetas = [(th0, th1, th2) for th0 in thetas0 for th1 in thetas1 for th2 in thetas2]
    #     return thetas

    def grid_search_theta_values(self, thetas0, thetas1, thetas2, thetas3): #. using vectors reduces loops in perform_grid_search_sample_paths()
        thetas = [(th0, th1, th2, th3) for th0 in thetas0 for th1 in thetas1 for th2 in thetas2 for th3 in thetas3]
        return thetas

    def plot_Fhat_map(self, Fhat__mean, thetasX, thetasY, labelX, labelY, title, theta__max_ELA, theta__max_SON):
        # Fhat_values = [FhatI_theta_I[(thetaX,thetaY)] for thetaY in thetasY for thetaX in thetasX]
        Fhat_values = [Fhat__mean[(thetaX,thetaY, theta__max_ELA,theta__max_SON)] for thetaY in thetasY for thetaX in thetasX]
        Fhats = np.array(Fhat_values)
        increment_count = len(thetasX)
        Fhats = np.reshape(Fhats, (-1, increment_count))
        fig, ax = plt.subplots()
        im = ax.imshow(Fhats, cmap='hot', origin='lower', aspect='auto')
        # create colorbar
        cbar = ax.figure.colorbar(im, ax=ax)
        # cbar.ax.set_ylabel(cbarlabel, rotation=-90, va="bottom")
        # we want to show all ticks...
        ax.set_xticks(np.arange(0,len(thetasX), 5))
        ax.set_yticks(np.arange(0,len(thetasY), 5))
        # ... and label them with the respective list entries
        ax.set_xticklabels(thetasX[::5])
        ax.set_yticklabels(thetasY[::5])
        # rotate the tick labels and set their alignment.
        #plt.setp(ax.get_xticklabels(), rotation=45, ha="right",rotation_mode="anchor")
        ax.set_title(title, fontsize=16)
        ax.set_xlabel(labelX)
        ax.set_ylabel(labelY)
        #fig.tight_layout()
        plt.show()
        return True

    def plot_Fhat_maps(self, 
          Fhat__mean, Fhat__stdv, 
          thetasX, thetasY, labelX, labelY, title_mean, title_stdv, 
          theta__max_ELA, theta__max_SON):
        # Fhat_values = [FhatI_theta_I[(thetaX,thetaY)] for thetaY in thetasY for thetaX in thetasX]
        Fhat_values = [Fhat__mean[(thetaX,thetaY, theta__max_ELA,theta__max_SON)] for thetaY in thetasY for thetaX in thetasX]
        Fhats = np.array(Fhat_values)
        increment_count = len(thetasX)
        Fhats = np.reshape(Fhats, (-1, increment_count))
        fig, ax = plt.subplots()
        im = ax.imshow(Fhats, cmap='hot', origin='lower', aspect='auto')
        # create colorbar
        cbar = ax.figure.colorbar(im, ax=ax)
        # cbar.ax.set_ylabel(cbarlabel, rotation=-90, va="bottom")
        # we want to show all ticks...
        ax.set_xticks(np.arange(0,len(thetasX), 5))
        ax.set_yticks(np.arange(0,len(thetasY), 5))
        # ... and label them with the respective list entries
        ax.set_xticklabels(thetasX[::5])
        ax.set_yticklabels(thetasY[::5])
        # rotate the tick labels and set their alignment.
        #plt.setp(ax.get_xticklabels(), rotation=45, ha="right",rotation_mode="anchor")
        ax.set_title(title_mean, fontsize=16)
        ax.set_xlabel(labelX)
        ax.set_ylabel(labelY)
        #fig.tight_layout()

        print()

        Fhat_values = [Fhat__stdv[(thetaX,thetaY, theta__max_ELA,theta__max_SON)] for thetaY in thetasY for thetaX in thetasX]
        Fhats = np.array(Fhat_values)
        increment_count = len(thetasX)
        Fhats = np.reshape(Fhats, (-1, increment_count))
        fig, ax = plt.subplots()
        im = ax.imshow(Fhats, cmap='hot', origin='lower', aspect='auto')
        # create colorbar
        cbar = ax.figure.colorbar(im, ax=ax)
        # cbar.ax.set_ylabel(cbarlabel, rotation=-90, va="bottom")
        # we want to show all ticks...
        ax.set_xticks(np.arange(0,len(thetasX), 5))
        ax.set_yticks(np.arange(0,len(thetasY), 5))
        # ... and label them with the respective list entries
        ax.set_xticklabels(thetasX[::5])
        ax.set_yticklabels(thetasY[::5])
        # rotate the tick labels and set their alignment.
        #plt.setp(ax.get_xticklabels(), rotation=45, ha="right",rotation_mode="anchor")
        ax.set_title(title_stdv, fontsize=16)
        ax.set_xlabel(labelX)
        ax.set_ylabel(labelY)
        #fig.tight_layout()

        plt.show()
        return True

    def plot_Fhat_chart(self, FhatI_theta_I, thetasX, labelX, labelY, title, color_style):
        mpl.rcParams['lines.linewidth'] = 1.2
        xylabelsize = 18
        plt.figure(figsize=(25, 8))
        plt.title(title, fontsize=20)
        Fhats = FhatI_theta_I.values()
        plt.plot(thetasX, Fhats, color_style)
        plt.xlabel(labelX, rotation=0, ha='right', va='center', fontweight='bold', size=xylabelsize)
        plt.ylabel(labelY, rotation=0, ha='right', va='center', fontweight='bold', size=xylabelsize)
        plt.show()

    def plot_train(self, df, policy, comment):
      # legendlabels = [r'$\mathrm{opt}$', r'$\mathrm{non}$']
      n_e = len(eNames) #number of entities
      n_charts = 2*n_e + 1 + 1#6
      ylabelsize = 16
      mpl.rcParams['lines.linewidth'] = 1.2
      # plt.rcParams['axes.prop_cycle'] = plt.cycler(color=['g', 'b', 'c', 'm'])
      # mycolors = {e: mycolors[i] for i,e in enumerate(eNames)}
      mycolors = ['g', 'b', 'c', 'm']
      fig, axs = plt.subplots(n_charts, sharex=True)
      fig.set_figwidth(13); fig.set_figheight(9)
      fig.suptitle(f'TRAINING OF {policy} POLICY'+'\n'+f'{comment}'+'\n'+f'L = {L}, T = {T}', fontsize=16)

      for xi,e in enumerate(eNames):
        axs[xi].set_ylim(auto=True); axs[xi].spines['top'].set_visible(False); axs[xi].spines['right'].set_visible(True); axs[xi].spines['bottom'].set_visible(False)
        axs[xi].step(df[f'x_t_{e}'], mycolors[xi%len(mycolors)])
        axs[xi].axhline(y=0, color='k', linestyle=':')
        axs[xi].set_ylabel('$x_{t,'+f'{e}'+'}$', rotation=0, ha='right', va='center', fontweight='bold', size=ylabelsize)
        for j in range(df.shape[0]//T): axs[xi].axvline(x=j*T, color='grey', ls=':')

      xi = n_e #xi: axis index, ci: chart index on same axis
      axs[xi].set_ylim(auto=True); axs[xi].spines['top'].set_visible(False); axs[xi].spines['right'].set_visible(True); axs[xi].spines['bottom'].set_visible(False)
      for ci,e in enumerate(eNames):
        axs[xi].step(df[f'D_t_{e}'], mycolors[ci])
        axs[xi].axhline(y=dem_sim.muD[e], color='g', linestyle=':')
        axs[xi].text(-4, dem_sim.muD[e], r'$\mu^{'+f'{e}'+'}$', size=16, color=mycolors[ci%len(mycolors)])
      axs[xi].set_ylabel('$D_{t,e}$'+'\n'+'$\mathrm{[units]}$', rotation=0, ha='right', va='center', fontweight='bold', size=ylabelsize)
      for j in range(df.shape[0]//T): axs[xi].axvline(x=j*T, color='grey', ls=':')    

      xi = n_e + 1
      for i,e in enumerate(eNames):
        axs[xi+i].set_ylim(auto=True); axs[xi+i].spines['top'].set_visible(False); axs[xi+i].spines['right'].set_visible(True); axs[xi+i].spines['bottom'].set_visible(False)
        axs[xi+i].step(df[f'R_t_{e}'], mycolors[i%len(mycolors)])
        axs[xi+i].axhline(y=0, color='k', linestyle=':')
        axs[xi+i].set_ylabel('$R_{t,'+f'{e}'+'}$', rotation=0, ha='right', va='center', fontweight='bold', size=ylabelsize)
        for j in range(df.shape[0]//T): axs[i].axvline(x=j*T, color='grey', ls=':')

      xi = 2*n_e + 1 #cumC
      axs[xi].set_ylim(auto=True); axs[xi].spines['top'].set_visible(False); axs[xi].spines['right'].set_visible(True); axs[xi].spines['bottom'].set_visible(False)
      axs[xi].step(df['cumC'], 'k')
      axs[xi].axhline(y=0, color='k', linestyle=':')
      axs[xi].set_ylabel('$\mathrm{cumC}$'+'\n'+'$\mathrm{(Profit)}$'+'\n'+''+'$\mathrm{[\$]}$', rotation=0, ha='right', va='center', fontweight='bold', size=ylabelsize);
      axs[xi].set_xlabel('$t\ \mathrm{[order\ windows]}$', rotation=0, ha='right', va='center', fontweight='bold', size=ylabelsize);
      for j in range(df.shape[0]//T): axs[i].axvline(x=j*T, color='grey', ls=':')

      # fig.legend(labels=legendlabels, loc='lower left', fontsize=16)

    def plot_evalu(self, df_non, df, thetaStar):
      legendlabels = [r'$\mathrm{opt}$', r'$\mathrm{non}$']
      n_e = len(eNames) #number of entities
      n_charts = 2*n_e + 1 + 1#6
      ylabelsize = 16
      mpl.rcParams['lines.linewidth'] = 1.2
      mycolors = ['g', 'b', 'c', 'm']
      fig, axs = plt.subplots(n_charts, sharex=True)
      # fig.set_figwidth(50); fig.set_figheight(10)
      fig.set_figwidth(13); fig.set_figheight(9)
      fig.suptitle(f'PERFORMANCE OF OPTIMIZED Buy-Below POLICY\nOptimal (magenta), Non-optimal (cyan), '+r'$\theta^*$'+f'= {thetaStar}', fontsize=16)

      for xi,e in enumerate(eNames):
        axs[xi].set_ylim(auto=True); axs[xi].spines['top'].set_visible(False); axs[xi].spines['right'].set_visible(True); axs[xi].spines['bottom'].set_visible(False)
        axs[xi].step(df['x_t_ELA'], 'm')
        axs[xi].step(df_non['x_t_ELA'], 'c')
        axs[xi].axhline(y=0, color='k', linestyle=':')
        axs[xi].set_ylabel('$x_{t,'+f'{e}'+'}$', rotation=0, ha='right', va='center', fontweight='bold', size=ylabelsize)

      xi = n_e #xi: axis index, ci: chart index on same axis
      axs[xi].set_ylim(auto=True); axs[xi].spines['top'].set_visible(False); axs[xi].spines['right'].set_visible(True); axs[xi].spines['bottom'].set_visible(False)
      for ci,e in enumerate(eNames):
        axs[xi].step(df[f'D_t_{e}'], mycolors[ci])
        axs[xi].text(-4, dem_sim.muD[e], r'$\mu^{'+f'{e}'+'}$', size=16, color=mycolors[ci%len(mycolors)])
        axs[xi].axhline(y=dem_sim.muD[e], color='g', linestyle=':')
      axs[xi].set_ylabel('$D_{t,e}$'+'\n'+'$\mathrm{[units]}$', rotation=0, ha='right', va='center', fontweight='bold', size=ylabelsize)

      xi = n_e + 1
      for i,e in enumerate(eNames):
        axs[xi+i].set_ylim(auto=True); axs[xi+i].spines['top'].set_visible(False); axs[xi+i].spines['right'].set_visible(True); axs[xi+i].spines['bottom'].set_visible(False)
        axs[xi+i].step(df[f'R_t_{e}'], 'm')
        axs[xi+i].text(-4, theta_evalu[i], r'$\theta^{buy'+f'{e}'+'}$'+f"={theta_evalu[i]}", size=16, color='m')
        axs[xi+i].axhline(y=theta_evalu[i], color='m', linestyle=':')
        axs[xi+i].step(df_non[f'R_t_{e}'], 'c')
        axs[xi+i].text(-4, theta_evalu_non[i], r'$\theta^{buy'+f'{e}'+'}$', size=16, color='c')
        axs[xi+i].axhline(y=theta_evalu_non[i], color='c', linestyle=':')
        axs[xi+i].text(22, theta_evalu[i+2], r'$R^{max'+f'{e}'+'}$'+f'{theta_evalu[i+2]}', size=16, color='k')
        axs[xi+i].axhline(y=theta_evalu[i+2], color='k', linestyle=':') #max spaces
        axs[xi+i].set_ylabel('$R_{t,'+f'{e}'+'}$'+'\n'+'$\mathrm{[units]}$', rotation=0, ha='right', va='center', fontweight='bold', size=ylabelsize)

      xi = 2*n_e + 1 #cumC
      axs[xi].set_ylim(auto=True); axs[xi].spines['top'].set_visible(False); axs[xi].spines['right'].set_visible(True); axs[xi].spines['bottom'].set_visible(False)
      axs[xi].step(df['cumC'], 'm')
      axs[xi].step(df_non['cumC'], 'c')
      axs[xi].set_ylabel('$\mathrm{cumC}$'+'\n'+'$\mathrm{(Profit)}$'+'\n'+''+'$\mathrm{[\$]}$', rotation=0, ha='right', va='center', fontweight='bold', size=ylabelsize)
      axs[xi].set_xlabel('$t\ \mathrm{[order\ windows]}$', rotation=0, ha='right', va='center', fontweight='bold', size=ylabelsize);

      fig.legend(labels=legendlabels, loc='lower left', fontsize=16)

4.6 Policy Evaluation

4.6.1 Training/Tuning

# UPDATE PARAMETERS
# T__sim = 100
L = 2*T__sim #number of sample-paths
T = T__sim #number of transitions/steps in each sample-path
# create a model, policy, and demand simulator
params.update({'Algorithm': 'GridSearch'}); pprint(f'{params=}')
params.update({'R_0': (0, 0)}) #for 'R_t_ELA', 'R_t_SON'
params.update({'eta': None})
exogParams = {}# we use simulation
possibleDecisions = None
M = InventoryStorageModel(
    SNames, 
    xNames, 
    eNames,
    params, 
    exogParams,
    possibleDecisions,
    p__buy,
    p__sell
)
M.S_0.update({
    'R_t': {'ELA': params['R_0'][0], 'SON': params['R_0'][1]},
    'D_t': {'ELA': 0, 'SON': 0}})
P = InventoryStoragePolicy(M, piNames)

dem_sim = DemandSimulator(
    T__sim=T__sim, 
    muD=muD,
    eventTimeD={'ELA': None, 'SON': None},
    muDeltaD={'ELA': None, 'SON': None},
)
("params={'Algorithm': 'GridSearch', 'T': 192, 'eta': 1, 'R__max': 57, 'R_0': "
 "0, 'seed': 189654913, 'theta_sell_min': 10, 'theta_sell_max': 100, "
 "'theta_buy_min': 10, 'theta_buy_max': 100, 'theta_inc': 1}")
L,T
(120, 60)
%%time
##########################################################################
#GridSearch #. SDAM-9.4.1
if params['Algorithm'] == 'GridSearch':
    thetasBuy = {'ELA': np.arange(10, 40, 1), 'SON': np.arange(10, 20, 1)}

    thetasMax = {'ELA': np.arange(10, 40, 1), 'SON': np.arange(10, 40, 1)}

    thetas = P.grid_search_theta_values(
        thetasBuy['ELA'], thetasBuy['SON'], thetasMax['ELA'], thetasMax['SON'])
    Fhat__mean_BuyBelow, Fhat__stdv_BuyBelow, thetaStar_BuyBelow, record_BuyBelow = \
      P.perform_grid_search_sample_paths(T, L, thetas, 'X__BuyBelow')
##################################################################################
... printing every 20th theta if considered ...
=== (820 / 270,000), theta=(10, 10, 37, 20) ===
=== (1,720 / 270,000), theta=(10, 11, 37, 20) ===
=== (2,620 / 270,000), theta=(10, 12, 37, 20) ===
=== (3,520 / 270,000), theta=(10, 13, 37, 20) ===
=== (4,420 / 270,000), theta=(10, 14, 37, 20) ===
=== (5,320 / 270,000), theta=(10, 15, 37, 20) ===
=== (6,220 / 270,000), theta=(10, 16, 37, 20) ===
=== (7,120 / 270,000), theta=(10, 17, 37, 20) ===
=== (8,020 / 270,000), theta=(10, 18, 37, 20) ===
=== (8,920 / 270,000), theta=(10, 19, 37, 20) ===
=== (9,820 / 270,000), theta=(11, 10, 37, 20) ===
=== (10,720 / 270,000), theta=(11, 11, 37, 20) ===
=== (11,620 / 270,000), theta=(11, 12, 37, 20) ===
=== (12,520 / 270,000), theta=(11, 13, 37, 20) ===
=== (13,420 / 270,000), theta=(11, 14, 37, 20) ===
=== (14,320 / 270,000), theta=(11, 15, 37, 20) ===
=== (15,220 / 270,000), theta=(11, 16, 37, 20) ===
=== (16,120 / 270,000), theta=(11, 17, 37, 20) ===
=== (17,020 / 270,000), theta=(11, 18, 37, 20) ===
=== (17,920 / 270,000), theta=(11, 19, 37, 20) ===
=== (18,820 / 270,000), theta=(12, 10, 37, 20) ===
=== (19,720 / 270,000), theta=(12, 11, 37, 20) ===
=== (20,620 / 270,000), theta=(12, 12, 37, 20) ===
=== (21,520 / 270,000), theta=(12, 13, 37, 20) ===
=== (22,420 / 270,000), theta=(12, 14, 37, 20) ===
=== (23,320 / 270,000), theta=(12, 15, 37, 20) ===
=== (24,220 / 270,000), theta=(12, 16, 37, 20) ===
=== (25,120 / 270,000), theta=(12, 17, 37, 20) ===
=== (26,020 / 270,000), theta=(12, 18, 37, 20) ===
=== (26,920 / 270,000), theta=(12, 19, 37, 20) ===
=== (27,820 / 270,000), theta=(13, 10, 37, 20) ===
=== (28,720 / 270,000), theta=(13, 11, 37, 20) ===
=== (29,620 / 270,000), theta=(13, 12, 37, 20) ===
=== (30,520 / 270,000), theta=(13, 13, 37, 20) ===
=== (31,420 / 270,000), theta=(13, 14, 37, 20) ===
=== (32,320 / 270,000), theta=(13, 15, 37, 20) ===
=== (33,220 / 270,000), theta=(13, 16, 37, 20) ===
=== (34,120 / 270,000), theta=(13, 17, 37, 20) ===
=== (35,020 / 270,000), theta=(13, 18, 37, 20) ===
=== (35,920 / 270,000), theta=(13, 19, 37, 20) ===
=== (36,820 / 270,000), theta=(14, 10, 37, 20) ===
=== (37,720 / 270,000), theta=(14, 11, 37, 20) ===
=== (38,620 / 270,000), theta=(14, 12, 37, 20) ===
=== (39,520 / 270,000), theta=(14, 13, 37, 20) ===
=== (40,420 / 270,000), theta=(14, 14, 37, 20) ===
=== (41,320 / 270,000), theta=(14, 15, 37, 20) ===
=== (42,220 / 270,000), theta=(14, 16, 37, 20) ===
=== (43,120 / 270,000), theta=(14, 17, 37, 20) ===
=== (44,020 / 270,000), theta=(14, 18, 37, 20) ===
=== (44,920 / 270,000), theta=(14, 19, 37, 20) ===
=== (45,820 / 270,000), theta=(15, 10, 37, 20) ===
=== (46,720 / 270,000), theta=(15, 11, 37, 20) ===
=== (47,620 / 270,000), theta=(15, 12, 37, 20) ===
=== (48,520 / 270,000), theta=(15, 13, 37, 20) ===
=== (49,420 / 270,000), theta=(15, 14, 37, 20) ===
=== (50,320 / 270,000), theta=(15, 15, 37, 20) ===
=== (51,220 / 270,000), theta=(15, 16, 37, 20) ===
=== (52,120 / 270,000), theta=(15, 17, 37, 20) ===
=== (53,020 / 270,000), theta=(15, 18, 37, 20) ===
=== (53,920 / 270,000), theta=(15, 19, 37, 20) ===
=== (54,820 / 270,000), theta=(16, 10, 37, 20) ===
=== (55,720 / 270,000), theta=(16, 11, 37, 20) ===
=== (56,620 / 270,000), theta=(16, 12, 37, 20) ===
=== (57,520 / 270,000), theta=(16, 13, 37, 20) ===
=== (58,420 / 270,000), theta=(16, 14, 37, 20) ===
=== (59,320 / 270,000), theta=(16, 15, 37, 20) ===
=== (60,220 / 270,000), theta=(16, 16, 37, 20) ===
=== (61,120 / 270,000), theta=(16, 17, 37, 20) ===
=== (62,020 / 270,000), theta=(16, 18, 37, 20) ===
=== (62,920 / 270,000), theta=(16, 19, 37, 20) ===
=== (63,820 / 270,000), theta=(17, 10, 37, 20) ===
=== (64,720 / 270,000), theta=(17, 11, 37, 20) ===
=== (65,620 / 270,000), theta=(17, 12, 37, 20) ===
=== (66,520 / 270,000), theta=(17, 13, 37, 20) ===
=== (67,420 / 270,000), theta=(17, 14, 37, 20) ===
=== (68,320 / 270,000), theta=(17, 15, 37, 20) ===
=== (69,220 / 270,000), theta=(17, 16, 37, 20) ===
=== (70,120 / 270,000), theta=(17, 17, 37, 20) ===
=== (71,020 / 270,000), theta=(17, 18, 37, 20) ===
=== (71,920 / 270,000), theta=(17, 19, 37, 20) ===
=== (72,820 / 270,000), theta=(18, 10, 37, 20) ===
=== (73,720 / 270,000), theta=(18, 11, 37, 20) ===
=== (74,620 / 270,000), theta=(18, 12, 37, 20) ===
=== (75,520 / 270,000), theta=(18, 13, 37, 20) ===
=== (76,420 / 270,000), theta=(18, 14, 37, 20) ===
=== (77,320 / 270,000), theta=(18, 15, 37, 20) ===
=== (78,220 / 270,000), theta=(18, 16, 37, 20) ===
=== (79,120 / 270,000), theta=(18, 17, 37, 20) ===
=== (80,020 / 270,000), theta=(18, 18, 37, 20) ===
=== (80,920 / 270,000), theta=(18, 19, 37, 20) ===
=== (81,820 / 270,000), theta=(19, 10, 37, 20) ===
=== (82,720 / 270,000), theta=(19, 11, 37, 20) ===
=== (83,620 / 270,000), theta=(19, 12, 37, 20) ===
=== (84,520 / 270,000), theta=(19, 13, 37, 20) ===
=== (85,420 / 270,000), theta=(19, 14, 37, 20) ===
=== (86,320 / 270,000), theta=(19, 15, 37, 20) ===
=== (87,220 / 270,000), theta=(19, 16, 37, 20) ===
=== (88,120 / 270,000), theta=(19, 17, 37, 20) ===
=== (89,020 / 270,000), theta=(19, 18, 37, 20) ===
=== (89,920 / 270,000), theta=(19, 19, 37, 20) ===
=== (90,820 / 270,000), theta=(20, 10, 37, 20) ===
=== (91,720 / 270,000), theta=(20, 11, 37, 20) ===
=== (92,620 / 270,000), theta=(20, 12, 37, 20) ===
=== (93,520 / 270,000), theta=(20, 13, 37, 20) ===
=== (94,420 / 270,000), theta=(20, 14, 37, 20) ===
=== (95,320 / 270,000), theta=(20, 15, 37, 20) ===
=== (96,220 / 270,000), theta=(20, 16, 37, 20) ===
=== (97,120 / 270,000), theta=(20, 17, 37, 20) ===
=== (98,020 / 270,000), theta=(20, 18, 37, 20) ===
=== (98,920 / 270,000), theta=(20, 19, 37, 20) ===
=== (99,820 / 270,000), theta=(21, 10, 37, 20) ===
=== (100,720 / 270,000), theta=(21, 11, 37, 20) ===
=== (101,620 / 270,000), theta=(21, 12, 37, 20) ===
=== (102,520 / 270,000), theta=(21, 13, 37, 20) ===
=== (103,420 / 270,000), theta=(21, 14, 37, 20) ===
=== (104,320 / 270,000), theta=(21, 15, 37, 20) ===
=== (105,220 / 270,000), theta=(21, 16, 37, 20) ===
=== (106,120 / 270,000), theta=(21, 17, 37, 20) ===
=== (107,020 / 270,000), theta=(21, 18, 37, 20) ===
=== (107,920 / 270,000), theta=(21, 19, 37, 20) ===
=== (108,820 / 270,000), theta=(22, 10, 37, 20) ===
=== (109,720 / 270,000), theta=(22, 11, 37, 20) ===
=== (110,620 / 270,000), theta=(22, 12, 37, 20) ===
=== (111,520 / 270,000), theta=(22, 13, 37, 20) ===
=== (112,420 / 270,000), theta=(22, 14, 37, 20) ===
=== (113,320 / 270,000), theta=(22, 15, 37, 20) ===
=== (114,220 / 270,000), theta=(22, 16, 37, 20) ===
=== (115,120 / 270,000), theta=(22, 17, 37, 20) ===
=== (116,020 / 270,000), theta=(22, 18, 37, 20) ===
=== (116,920 / 270,000), theta=(22, 19, 37, 20) ===
=== (117,820 / 270,000), theta=(23, 10, 37, 20) ===
=== (118,720 / 270,000), theta=(23, 11, 37, 20) ===
=== (119,620 / 270,000), theta=(23, 12, 37, 20) ===
=== (120,520 / 270,000), theta=(23, 13, 37, 20) ===
=== (121,420 / 270,000), theta=(23, 14, 37, 20) ===
=== (122,320 / 270,000), theta=(23, 15, 37, 20) ===
=== (123,220 / 270,000), theta=(23, 16, 37, 20) ===
=== (124,120 / 270,000), theta=(23, 17, 37, 20) ===
=== (125,020 / 270,000), theta=(23, 18, 37, 20) ===
=== (125,920 / 270,000), theta=(23, 19, 37, 20) ===
=== (126,820 / 270,000), theta=(24, 10, 37, 20) ===
=== (127,720 / 270,000), theta=(24, 11, 37, 20) ===
=== (128,620 / 270,000), theta=(24, 12, 37, 20) ===
=== (129,520 / 270,000), theta=(24, 13, 37, 20) ===
=== (130,420 / 270,000), theta=(24, 14, 37, 20) ===
=== (131,320 / 270,000), theta=(24, 15, 37, 20) ===
=== (132,220 / 270,000), theta=(24, 16, 37, 20) ===
=== (133,120 / 270,000), theta=(24, 17, 37, 20) ===
=== (134,020 / 270,000), theta=(24, 18, 37, 20) ===
=== (134,920 / 270,000), theta=(24, 19, 37, 20) ===
=== (135,820 / 270,000), theta=(25, 10, 37, 20) ===
=== (136,720 / 270,000), theta=(25, 11, 37, 20) ===
=== (137,620 / 270,000), theta=(25, 12, 37, 20) ===
=== (138,520 / 270,000), theta=(25, 13, 37, 20) ===
=== (139,420 / 270,000), theta=(25, 14, 37, 20) ===
=== (140,320 / 270,000), theta=(25, 15, 37, 20) ===
=== (141,220 / 270,000), theta=(25, 16, 37, 20) ===
=== (142,120 / 270,000), theta=(25, 17, 37, 20) ===
=== (143,020 / 270,000), theta=(25, 18, 37, 20) ===
=== (143,920 / 270,000), theta=(25, 19, 37, 20) ===
=== (144,820 / 270,000), theta=(26, 10, 37, 20) ===
=== (145,720 / 270,000), theta=(26, 11, 37, 20) ===
=== (146,620 / 270,000), theta=(26, 12, 37, 20) ===
=== (147,520 / 270,000), theta=(26, 13, 37, 20) ===
=== (148,420 / 270,000), theta=(26, 14, 37, 20) ===
=== (149,320 / 270,000), theta=(26, 15, 37, 20) ===
=== (150,220 / 270,000), theta=(26, 16, 37, 20) ===
=== (151,120 / 270,000), theta=(26, 17, 37, 20) ===
=== (152,020 / 270,000), theta=(26, 18, 37, 20) ===
=== (152,920 / 270,000), theta=(26, 19, 37, 20) ===
=== (153,820 / 270,000), theta=(27, 10, 37, 20) ===
=== (154,720 / 270,000), theta=(27, 11, 37, 20) ===
=== (155,620 / 270,000), theta=(27, 12, 37, 20) ===
=== (156,520 / 270,000), theta=(27, 13, 37, 20) ===
=== (157,420 / 270,000), theta=(27, 14, 37, 20) ===
=== (158,320 / 270,000), theta=(27, 15, 37, 20) ===
=== (159,220 / 270,000), theta=(27, 16, 37, 20) ===
=== (160,120 / 270,000), theta=(27, 17, 37, 20) ===
=== (161,020 / 270,000), theta=(27, 18, 37, 20) ===
=== (161,920 / 270,000), theta=(27, 19, 37, 20) ===
=== (162,820 / 270,000), theta=(28, 10, 37, 20) ===
=== (163,720 / 270,000), theta=(28, 11, 37, 20) ===
=== (164,620 / 270,000), theta=(28, 12, 37, 20) ===
=== (165,520 / 270,000), theta=(28, 13, 37, 20) ===
=== (166,420 / 270,000), theta=(28, 14, 37, 20) ===
=== (167,320 / 270,000), theta=(28, 15, 37, 20) ===
=== (168,220 / 270,000), theta=(28, 16, 37, 20) ===
=== (169,120 / 270,000), theta=(28, 17, 37, 20) ===
=== (170,020 / 270,000), theta=(28, 18, 37, 20) ===
=== (170,920 / 270,000), theta=(28, 19, 37, 20) ===
=== (171,820 / 270,000), theta=(29, 10, 37, 20) ===
=== (172,720 / 270,000), theta=(29, 11, 37, 20) ===
=== (173,620 / 270,000), theta=(29, 12, 37, 20) ===
=== (174,520 / 270,000), theta=(29, 13, 37, 20) ===
=== (175,420 / 270,000), theta=(29, 14, 37, 20) ===
=== (176,320 / 270,000), theta=(29, 15, 37, 20) ===
=== (177,220 / 270,000), theta=(29, 16, 37, 20) ===
=== (178,120 / 270,000), theta=(29, 17, 37, 20) ===
=== (179,020 / 270,000), theta=(29, 18, 37, 20) ===
=== (179,920 / 270,000), theta=(29, 19, 37, 20) ===
=== (180,820 / 270,000), theta=(30, 10, 37, 20) ===
=== (181,720 / 270,000), theta=(30, 11, 37, 20) ===
=== (182,620 / 270,000), theta=(30, 12, 37, 20) ===
=== (183,520 / 270,000), theta=(30, 13, 37, 20) ===
=== (184,420 / 270,000), theta=(30, 14, 37, 20) ===
=== (185,320 / 270,000), theta=(30, 15, 37, 20) ===
=== (186,220 / 270,000), theta=(30, 16, 37, 20) ===
=== (187,120 / 270,000), theta=(30, 17, 37, 20) ===
=== (188,020 / 270,000), theta=(30, 18, 37, 20) ===
=== (188,920 / 270,000), theta=(30, 19, 37, 20) ===
=== (189,820 / 270,000), theta=(31, 10, 37, 20) ===
=== (190,720 / 270,000), theta=(31, 11, 37, 20) ===
=== (191,620 / 270,000), theta=(31, 12, 37, 20) ===
=== (192,520 / 270,000), theta=(31, 13, 37, 20) ===
=== (193,420 / 270,000), theta=(31, 14, 37, 20) ===
=== (194,320 / 270,000), theta=(31, 15, 37, 20) ===
=== (195,220 / 270,000), theta=(31, 16, 37, 20) ===
=== (196,120 / 270,000), theta=(31, 17, 37, 20) ===
=== (197,020 / 270,000), theta=(31, 18, 37, 20) ===
=== (197,920 / 270,000), theta=(31, 19, 37, 20) ===
=== (198,820 / 270,000), theta=(32, 10, 37, 20) ===
=== (199,720 / 270,000), theta=(32, 11, 37, 20) ===
=== (200,620 / 270,000), theta=(32, 12, 37, 20) ===
=== (201,520 / 270,000), theta=(32, 13, 37, 20) ===
=== (202,420 / 270,000), theta=(32, 14, 37, 20) ===
=== (203,320 / 270,000), theta=(32, 15, 37, 20) ===
=== (204,220 / 270,000), theta=(32, 16, 37, 20) ===
=== (205,120 / 270,000), theta=(32, 17, 37, 20) ===
=== (206,020 / 270,000), theta=(32, 18, 37, 20) ===
=== (206,920 / 270,000), theta=(32, 19, 37, 20) ===
=== (207,820 / 270,000), theta=(33, 10, 37, 20) ===
=== (208,720 / 270,000), theta=(33, 11, 37, 20) ===
=== (209,620 / 270,000), theta=(33, 12, 37, 20) ===
=== (210,520 / 270,000), theta=(33, 13, 37, 20) ===
=== (211,420 / 270,000), theta=(33, 14, 37, 20) ===
=== (212,320 / 270,000), theta=(33, 15, 37, 20) ===
=== (213,220 / 270,000), theta=(33, 16, 37, 20) ===
=== (214,120 / 270,000), theta=(33, 17, 37, 20) ===
=== (215,020 / 270,000), theta=(33, 18, 37, 20) ===
=== (215,920 / 270,000), theta=(33, 19, 37, 20) ===
=== (216,820 / 270,000), theta=(34, 10, 37, 20) ===
=== (217,720 / 270,000), theta=(34, 11, 37, 20) ===
=== (218,620 / 270,000), theta=(34, 12, 37, 20) ===
=== (219,520 / 270,000), theta=(34, 13, 37, 20) ===
=== (220,420 / 270,000), theta=(34, 14, 37, 20) ===
=== (221,320 / 270,000), theta=(34, 15, 37, 20) ===
=== (222,220 / 270,000), theta=(34, 16, 37, 20) ===
=== (223,120 / 270,000), theta=(34, 17, 37, 20) ===
=== (224,020 / 270,000), theta=(34, 18, 37, 20) ===
=== (224,920 / 270,000), theta=(34, 19, 37, 20) ===
=== (225,820 / 270,000), theta=(35, 10, 37, 20) ===
=== (226,720 / 270,000), theta=(35, 11, 37, 20) ===
=== (227,620 / 270,000), theta=(35, 12, 37, 20) ===
=== (228,520 / 270,000), theta=(35, 13, 37, 20) ===
=== (229,420 / 270,000), theta=(35, 14, 37, 20) ===
=== (230,320 / 270,000), theta=(35, 15, 37, 20) ===
=== (231,220 / 270,000), theta=(35, 16, 37, 20) ===
=== (232,120 / 270,000), theta=(35, 17, 37, 20) ===
=== (233,020 / 270,000), theta=(35, 18, 37, 20) ===
=== (233,920 / 270,000), theta=(35, 19, 37, 20) ===
=== (234,820 / 270,000), theta=(36, 10, 37, 20) ===
=== (235,720 / 270,000), theta=(36, 11, 37, 20) ===
=== (236,620 / 270,000), theta=(36, 12, 37, 20) ===
=== (237,520 / 270,000), theta=(36, 13, 37, 20) ===
=== (238,420 / 270,000), theta=(36, 14, 37, 20) ===
=== (239,320 / 270,000), theta=(36, 15, 37, 20) ===
=== (240,220 / 270,000), theta=(36, 16, 37, 20) ===
=== (241,120 / 270,000), theta=(36, 17, 37, 20) ===
=== (242,020 / 270,000), theta=(36, 18, 37, 20) ===
=== (242,920 / 270,000), theta=(36, 19, 37, 20) ===
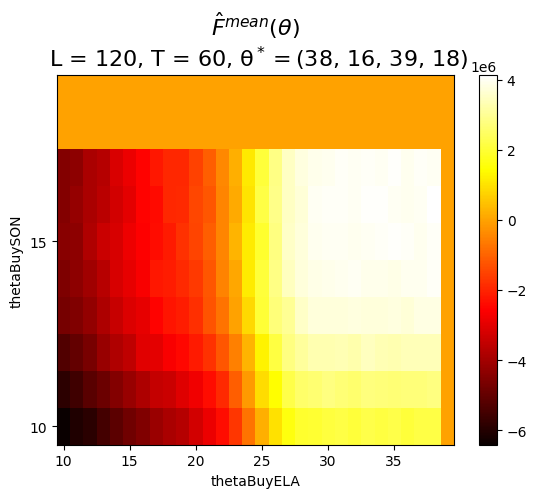
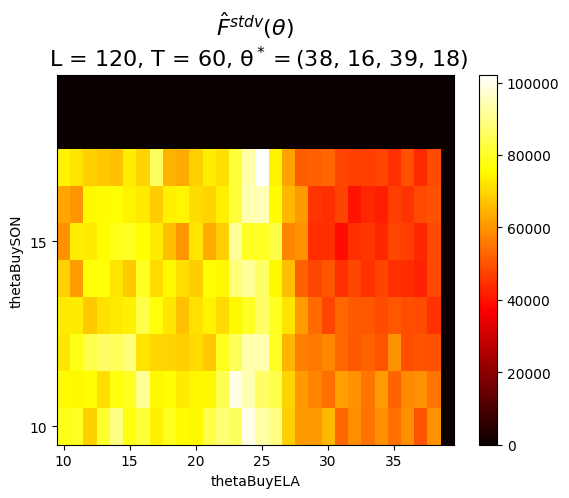
Finishing GridSearch in 948.47 secs
Best theta: (38, 16, 39, 18). Best cumC: 4,135,296.250000002
CPU times: user 15min 25s, sys: 11.8 s, total: 15min 37s
Wall time: 15min 48s
P.plot_Fhat_maps(
    Fhat__mean_BuyBelow, 
    Fhat__stdv_BuyBelow, 
    thetasBuy['ELA'], 
    thetasBuy['SON'], 
    'thetaBuyELA', 
    'thetaBuySON', 
    r"$\hat{F}^{mean}(\theta)$"+f"\n L = {L}, T = {T}, "+r"$\mathrm{\theta^*} =$"+f"{thetaStar_BuyBelow}",
    r"$\hat{F}^{stdv}(\theta)$"+f"\n L = {L}, T = {T}, "+r"$\mathrm{\theta^*} =$"+f"{thetaStar_BuyBelow}",
    thetaStar_BuyBelow[2],
    thetaStar_BuyBelow[3],
)

True
R_t_labels = ['R_t_'+e for e in eNames]
D_t_labels = ['D_t_'+e for e in eNames]
x_t_labels = ['x_t_'+e for e in eNames]
labels = ['piName', 'theta', 'l'] + \
  ['t'] + R_t_labels + D_t_labels + ['cumC'] + x_t_labels
# labels
f'{len(record_BuyBelow):,}', L, T
('28,684,800', 120, 60)
df_X__BuyBelow = pd.DataFrame.from_records(record_BuyBelow[:200], columns=labels)
# df_X__BuyBelow = pd.DataFrame.from_records(record_BuyBelow[-100:], columns=labels)
P.plot_train(df_X__BuyBelow, 'Buy-Below', '(first 200 records)')
df_X__BuyBelow.head()
piName theta l t R_t_ELA R_t_SON D_t_ELA D_t_SON cumC x_t_ELA x_t_SON
0 X__BuyBelow (10, 10, 18, 39) 1 0 18 39 17 8 -592,545.6500 18 39
1 X__BuyBelow (10, 10, 18, 39) 1 1 1 31 12 7 -378,561.3000 0 0
2 X__BuyBelow (10, 10, 18, 39) 1 2 17 24 16 7 -398,796.9500 17 0
3 X__BuyBelow (10, 10, 18, 39) 1 3 1 17 26 8 -157,562.6000 0 0
4 X__BuyBelow (10, 10, 18, 39) 1 4 17 9 20 6 -510,158.2500 17 0 

# df_X__BuyBelow = pd.DataFrame.from_records(record[:100], columns=labels)
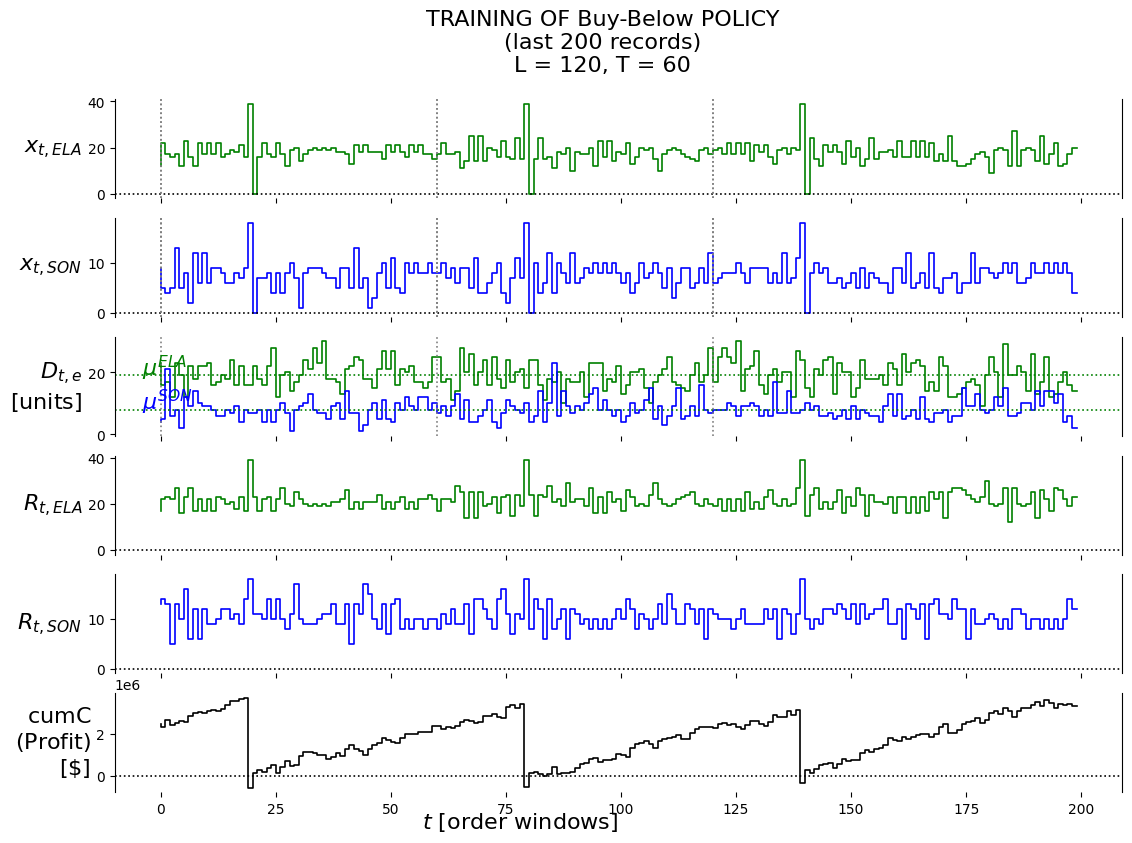
df_X__BuyBelow = pd.DataFrame.from_records(record_BuyBelow[-200:], columns=labels)
P.plot_train(df_X__BuyBelow, 'Buy-Below', '(last 200 records)')
df_X__BuyBelow.head()
piName theta l t R_t_ELA R_t_SON D_t_ELA D_t_SON cumC x_t_ELA x_t_SON
0 X__BuyBelow (38, 17, 39, 18) 117 40 17 13 23 4 2,490,238.3500 12 9
1 X__BuyBelow (38, 17, 39, 18) 117 41 22 14 16 5 2,325,852.7000 22 5
2 X__BuyBelow (38, 17, 39, 18) 117 42 23 13 17 21 2,662,357.0500 17 4
3 X__BuyBelow (38, 17, 39, 18) 117 43 22 5 12 6 2,442,711.4000 16 5
4 X__BuyBelow (38, 17, 39, 18) 117 44 27 13 23 8 2,557,635.7500 17 13

4.6.2 Evaluation

# EVALUATION
piName_evalu = 'X__BuyBelow'
stop_time_evalu = T__sim
M_evalu = InventoryStorageModel(
    SNames, 
    xNames, 
    eNames,
    params, 
    exogParams,
    possibleDecisions,
    p__buy,
    p__sell    
)
M_evalu.S_0.update({
    'R_t': {'ELA': params['R_0'][0], 'SON': params['R_0'][1]},
    'D_t': {'ELA': 0, 'SON': 0}})
P_evalu = InventoryStoragePolicy(M_evalu, piNames)

dem_sim = DemandSimulator(
    T__sim=T__sim, 
    muD=muD, #19, 8
    eventTimeD={'ELA': None, 'SON': None},
    muDeltaD={'ELA': None, 'SON': None},
)
def run_policy_evalu(piInfo_evalu, piName_evalu, stop_time_evalu, model_copy):
    record = []
    for t in range(stop_time_evalu):
        x_t = getattr(P_evalu, piName_evalu)(t, model_copy.S_t, piInfo_evalu, stop_time_evalu)
        S_t, cumC, x_t = model_copy.step(t, x_t) # step the model forward one iteration
        record_t = \
          [S_t.R_t[e] for e in eNames] + \
          [S_t.D_t[e] for e in eNames] + \
          [cumC] + \
          [x_t.x_t[e] for e in eNames]
        record.append(record_t)
    cumC = model_copy.cumC    
    return cumC, record
4.6.2.1 Evalutate with data similar to train data
4.6.2.1.1 Non-optimal policy
# theta_evalu_non=(3, 3)
# theta_evalu_non=(10, 10, 11, 11)
theta_evalu_non=(20, 10, 40, 17)
piName_evalu_non = 'X__BuyBelow'
cumC, record = run_policy_evalu(theta_evalu_non, piName_evalu_non, stop_time_evalu, copy(M_evalu))
labels = ['R_t_ELA', 'R_t_SON', 'D_t_ELA', 'D_t_SON', "cumC", 'x_t_ELA', 'x_t_SON']
print(f'{theta_evalu_non=}')
print(f'{int(cumC)=:,}')
df_non = pd.DataFrame.from_records(data=record, columns=labels); df_non[:10]
theta_evalu_non=(20, 10, 40, 17)
int(cumC)=-2,767,808
R_t_ELA R_t_SON D_t_ELA D_t_SON cumC x_t_ELA x_t_SON
0 40 17 15 8 -577,885.6500 40 17
1 25 9 25 8 226,628.7000 0 0
2 0 9 19 9 294,843.0500 0 8
3 40 8 20 5 -494,472.6000 40 8
4 20 12 35 10 48,291.7500 0 9
5 20 2 20 7 -166,093.9000 20 0
6 20 15 20 13 -196,429.5500 20 15
7 20 2 24 9 -58,765.2000 20 0
8 20 15 18 8 -420,670.8500 20 15
9 22 7 26 12 -99,816.5000 20 0
4.6.2.1.2 Optimal policy
theta_evalu = thetaStar_BuyBelow
piName_evalu = 'X__BuyBelow'
cumC, record = run_policy_evalu(theta_evalu, piName_evalu, stop_time_evalu, copy(M_evalu))
labels = ['R_t_ELA', 'R_t_SON', 'D_t_ELA', 'D_t_SON', "cumC", 'x_t_ELA', 'x_t_SON']
print(f'{theta_evalu=}')
print(f'{int(cumC)=:,}')
df = pd.DataFrame.from_records(data=record, columns=labels); df[:10]
theta_evalu=(38, 16, 39, 18)
int(cumC)=4,150,531
R_t_ELA R_t_SON D_t_ELA D_t_SON cumC x_t_ELA x_t_SON
0 39 18 14 10 -549,655.6500 39 18
1 25 8 18 10 90,568.7000 0 0
2 21 10 16 5 56,403.0500 14 10
3 23 13 12 7 4,357.4000 18 8
4 27 11 18 3 89,031.7500 16 5
5 21 15 18 5 261,206.1000 12 7
6 21 13 17 9 491,510.4500 18 3
7 22 9 20 7 693,524.8000 18 5
8 19 11 18 6 752,249.1500 17 9
9 21 12 26 4 813,183.5000 20 7 
P.plot_evalu(df_non, df, thetaStar_BuyBelow)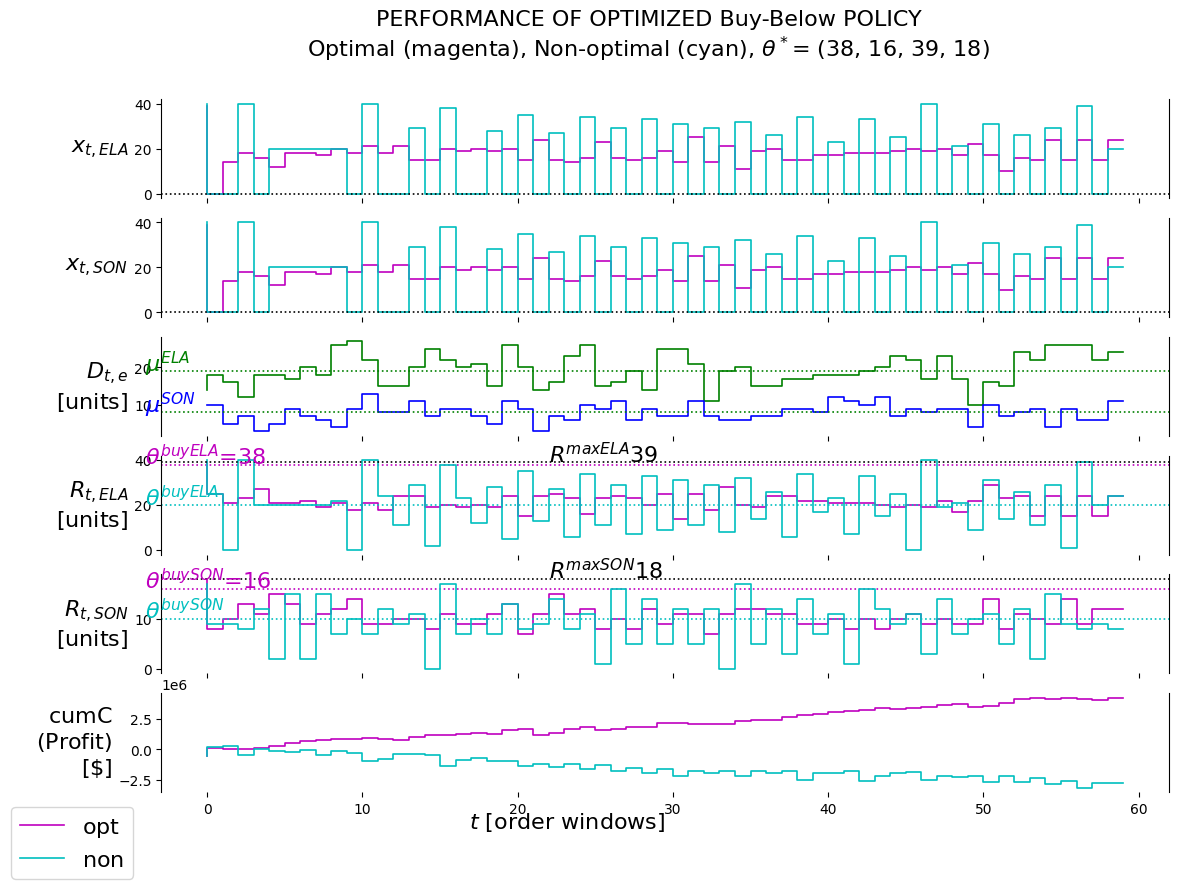

From the cumC plot we see that the cumulative reward for the optimal policy keeps on rising. The non-optimal, status-quo policy keeps losing money. Mr. Optimal currently has a partitioning of 40/17 spaces for Elantras/Sonatas. When levels fall below 20/10 he reorders up to 40/17. The optimal policy prescribes that Elantras/Sonatas should be partitioned 39/18 and ordered up to 38/16. Overall, it must be encouraging for Mr. Optimal that his partitioning was not too far from optimal. However, if he changes to the optimal policy, he stands to gain about a 175% improvement in profitability over a 100 order windows.