An RL Approach for Inventory Management (Part 6)

Tabular as a Form of Function Approximation

Inventory Management
Markov Decision Process
Python
Author

Kobus Esterhuysen

Published

July 14, 2022

1 Tabular as a Form of FunctionApprox

We now take a step back. Let us again consider a finite set of \(x\)-values \(\mathcal X={x_1,x_2,...,x_n}\). We further assume that all data sets consisting of \((x,y)\) pairs that we use have all their \(x\)-values inside this finite set \(\mathcal X\). We want to have \(\hat y = \mathbb E[y|x]\) such that - the prediction for this \(x\) is only calculated from the \(y\)-values in the data set associated with this \(x\) - the \(y\)-values in the data set associated with other \(x\)-values should not influence the prediction for this \(x\) - the prediction for this \(x\) is a kind of average of all the \(y\)-values associated with this \(x\)

We refer to this kind of setup as Tabular - each \(x \in \mathcal X\) can be stored in a table associated with its corresponding prediction \(\mathbb E[y|x]\).

!python --version
Python 3.7.15

We make use of the approach followed in http://web.stanford.edu/class/cme241/.

from __future__ import annotations
from typing import Tuple, Sequence, Iterator, List, TypeVar, Generic, overload
from scipy.stats import norm
import numpy as np
from abc import ABC, abstractmethod
from collections import defaultdict
from dataclasses import dataclass, replace, field
import itertools

2 Example Model Data Generator

Let’s setup a Data Model: \[ \begin{aligned} y &= \alpha + \beta_1 x_1 + \beta_2x_2 - \beta_3x_3 + \mathcal N(0, 2.0) \\ &= 2 + 10x_1 + 4x_2 - 6x_3 + \mathcal N(0, 2.0) \end{aligned} \]

Triple = Tuple[float, float, float]
Aug_Triple = Tuple[float, float, float, float] #. augmented to prepend bias
DataSeq = Sequence[Tuple[Triple, float]] #. last float is for y
def example_model_data_generator() -> Iterator[DataSeq]:
    coeffs: Aug_Triple = (2., 10., 4., -6.)
    values = np.linspace(-10.0, 10.0, 21)
    pts: Sequence[Triple] = [(x, y, z) for x in values for y in values
                             for z in values]
    d = norm(loc=0., scale=2.0) #. normal distribution
    while True:
        res: List[Tuple[Triple, float]] = []
        for pt in pts:
          # pt: np.ndarray = np.random.randn(3)
          x_val: Triple = (pt[0], pt[1], pt[2])
          y_val: float = coeffs[0] + np.dot(coeffs[1:], pt) + \
            d.rvs(size=1)[0]
          res.append((x_val, y_val))
        yield res
data_gen: Iterator[DataSeq] = example_model_data_generator(); data_gen
<generator object example_model_data_generator at 0x7f037d757b50>
next(data_gen)[:10]
[((-10.0, -10.0, -10.0), -79.48767732128363),
 ((-10.0, -10.0, -9.0), -82.06969223580259),
 ((-10.0, -10.0, -8.0), -88.14484959324732),
 ((-10.0, -10.0, -7.0), -98.79564553233163),
 ((-10.0, -10.0, -6.0), -100.54401550033428),
 ((-10.0, -10.0, -5.0), -108.94733942986316),
 ((-10.0, -10.0, -4.0), -114.67929646511288),
 ((-10.0, -10.0, -3.0), -122.14685477082418),
 ((-10.0, -10.0, -2.0), -127.84849723837867),
 ((-10.0, -10.0, -1.0), -131.72740725100914)]

3. Implement \(f(x; w)\)

We define the next class to implement the function approximation \(f(x;w)\). This class is generic in X to allow for arbitrary data types \(\mathcal X\). An instance of this class approximates a function \(x ↦ \mathbb R\). It enables: - evaluation of \(f(x;w)\) at specific predictor points - updating with additional \((x,\mathbb R)\) data points

X = TypeVar('X') #. for arbitrary data types scriptX
F = TypeVar('F', bound='FunctionApprox')
SMALL_NUM = 1e-6

class FunctionApprox(ABC, Generic[X]):
    @abstractmethod
    def __add__(self: F, other: F) -> F:
        pass

    @abstractmethod
    def __mul__(self: F, scalar: float) -> F:
        pass

    @abstractmethod
    def objective_gradient(
        self: F,
        xy_vals_seq: Iterable[Tuple[X, float]],
        obj_deriv_out_fun: Callable[[Sequence[X], Sequence[float]], np.ndarray]
    ) -> Gradient[F]:
      pass

    @abstractmethod
    def evaluate(self, x_values_seq: Iterable[X]) -> np.ndarray:
      pass

    def __call__(self, x_value: X) -> float:
        return self.evaluate([x_value]).item()

    @abstractmethod
    def update_with_gradient(
        self: F,
        gradient: Gradient[F]
    ) -> F:
      pass

    def update(
        self: F,
        xy_vals_seq: Iterable[Tuple[X, float]]
    ) -> F:
        def deriv_func(x: Sequence[X], y: Sequence[float]) -> np.ndarray:
            return self.evaluate(x) - np.array(y)

        return self.update_with_gradient(
            self.objective_gradient(xy_vals_seq, deriv_func)
        )

    @abstractmethod
    def solve(
        self: F,
        xy_vals_seq: Iterable[Tuple[X, float]],
        error_tolerance: Optional[float] = None
    ) -> F:
      pass

    @abstractmethod
    def within(self: F, other: F, tolerance: float) -> bool:
      pass

    def iterate_updates(
        self: F,
        xy_seq_stream: Iterator[Iterable[Tuple[X, float]]]
    ) -> Iterator[F]:
        return iterate.accumulate(
            xy_seq_stream,
            lambda fa, xy: fa.update(xy),
            initial=self
        )

    def rmse(
        self,
        xy_vals_seq: Iterable[Tuple[X, float]]
    ) -> float:
        x_seq, y_seq = zip(*xy_vals_seq)
        errors: np.ndarray = self.evaluate(x_seq) - np.array(y_seq)
        return np.sqrt(np.mean(errors * errors))

    def argmax(self, xs: Iterable[X]) -> X:
        args: Sequence[X] = list(xs)
        return args[np.argmax(self.evaluate(args))]

4. Implement Tabular

Now we implement the main class of this project: Tabular. A tabular prediction fits well into the interface of FunctionApprox. By considering tabular prediction as a special case of the class FunctionApprox, we can cast the

  • Tabular DP algorithms as special cases of the function approximation versions of the algorithms
  • Tabular RL algorithms as special cases of the function approximation versions of the algorithms We do all this by using the Tabular class.

The Tabular class approximates a function with a discrete domain (X), without interpolation. The value for each X is maintained as a weighted average of observations based on recency (tracked by count_to_weight_func).

So here is the implementation of this class:

@dataclass(frozen=True)
class Tabular(FunctionApprox[X]):
    values_map: Mapping[X, float] = field(default_factory=lambda: {})
    counts_map: Mapping[X, int] = field(default_factory=lambda: {})
    count_to_weight_func: Callable[[int], float] = \
        field(default_factory=lambda: lambda n: 1.0 / n)

    def objective_gradient( #. scriptG(w_t)
        self,
        xy_vals_seq: Iterable[Tuple[X, float]],
        obj_deriv_out_fun: Callable[[Sequence[X], Sequence[float]], float]
    ) -> Gradient[Tabular[X]]:
        x_vals, y_vals = zip(*xy_vals_seq)
        obj_deriv_out: np.ndarray = obj_deriv_out_fun(x_vals, y_vals)
        sums_map: Dict[X, float] = defaultdict(float)
        counts_map: Dict[X, int] = defaultdict(int)
        for x, o in zip(x_vals, obj_deriv_out):
            sums_map[x] += o
            counts_map[x] += 1
        return Gradient(replace(
            self,
            values_map={x: sums_map[x] / counts_map[x] for x in sums_map},
            counts_map=counts_map
        ))

    def __add__(self, other: Tabular[X]) -> Tabular[X]:
        values_map: Dict[X, float] = {}
        counts_map: Dict[X, int] = {}
        for key in set.union(
                set(self.values_map.keys()),
                set(other.values_map.keys())
        ):
            values_map[key] = self.values_map.get(key, 0.) + \
                other.values_map.get(key, 0.)
            counts_map[key] = counts_map.get(key, 0) + \
                other.counts_map.get(key, 0)
        return replace(
            self,
            values_map=values_map,
            counts_map=counts_map
        )

    def __mul__(self, scalar: float) -> Tabular[X]:
        return replace(
            self,
            values_map={x: scalar*y for x, y in self.values_map.items()}
        )

    def evaluate(self, x_values_seq: Iterable[X]) -> np.ndarray:
        return np.array([self.values_map.get(x, 0.) for x in x_values_seq])

    def update_with_gradient(
        self,
        gradient: Gradient[Tabular[X]]
    ) -> Tabular[X]:
        values_map: Dict[X, float] = dict(self.values_map)
        counts_map: Dict[X, int] = dict(self.counts_map)
        for key in gradient.function_approx.values_map:
            counts_map[key] = counts_map.get(key, 0) + \
                gradient.function_approx.counts_map[key]
            weight: float = self.count_to_weight_func(counts_map[key])
            values_map[key] = values_map.get(key, 0.) - \
                weight * gradient.function_approx.values_map[key]
        return replace(
            self,
            values_map=values_map,
            counts_map=counts_map
        )

    def solve(
        self,
        xy_vals_seq: Iterable[Tuple[X, float]],
        error_tolerance: Optional[float] = None
    ) -> Tabular[X]:
        values_map: Dict[X, float] = {}
        counts_map: Dict[X, int] = {}
        for x, y in xy_vals_seq:
            counts_map[x] = counts_map.get(x, 0) + 1
            weight: float = self.count_to_weight_func(counts_map[x])
            values_map[x] = weight * y + (1 - weight) * values_map.get(x, 0.)
        return replace(
            self,
            values_map=values_map,
            counts_map=counts_map
        )

    def within(self, other: FunctionApprox[X], tolerance: float) -> bool:
        if isinstance(other, Tabular):
            return all(abs(self.values_map[s] - other.values_map.get(s, 0.))
                       <= tolerance for s in self.values_map)
        return False

The attributes are: - values_map: Mapping[X, float] - mapping from each \(x\)-value to the average of the \(y\)-values associated with \(x\) that have been seen so far - counts_map: Mapping[X, int] - mapping from each \(x\)-value to the count of \(y\)-values associated with \(x\) that have been seen so far - count_to_weight_func: Callable[[int], float] - defines a function from number of \(y\)-values seen so far for each \(x\), to the weight assigned to the most recent \(y\).

The most important methods are: - solve - calculate the average of all the \(y\)-values associated with each \(x\) in the provided data set and store it in a table - inputs - xy_vals_seq: Iterable[Tuple[X, float]] - error_tolerance: Optional[float]=None - output - Tabular[X] - update - Update the FunctionApprox’s internal parameters \(w\) defined in \(f(x;w)\) based on incremental data supplied as \((x,y)\) pairs in the xy_vals_seq data structure. - inputs - xy_vals_seq: Iterable[Tuple[X, float]]
- the \((x,y)\) pairs in the current iteration - ouputs - F - the FunctionApprox \(f(x;w)\) corresponding to the updated parameters - evaluate - Evaluate the function approximation by looking up the value in the mapping for each state. If an X value has not been seen before and hence not initialized,returns 0 - inputs - x_values_seq: Iterable[X] - output - np.ndarray

The Gradient class holds the FunctionApprox F:

@dataclass(frozen=True)
class Gradient(Generic[F]):
    function_approx: F

    @overload
    def __add__(self, x: Gradient[F]) -> Gradient[F]:
        ...

    @overload
    def __add__(self, x: F) -> F:
        ...

    def __add__(self, x):
        if isinstance(x, Gradient):
            return Gradient(self.function_approx + x.function_approx)
        return self.function_approx + x

    def __mul__(self: Gradient[F], x: float) -> Gradient[F]:
        return Gradient(self.function_approx*x)

    def zero(self) -> Gradient[F]:
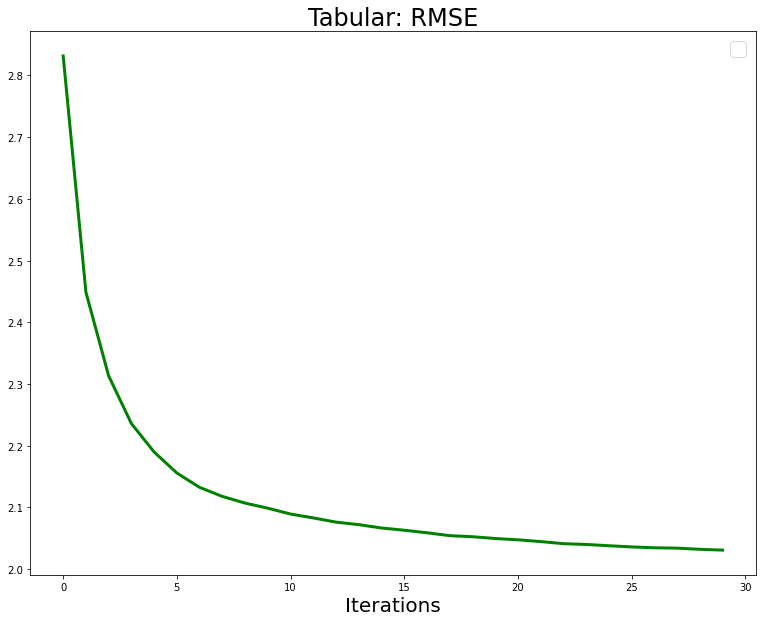
        return Gradient(self.function_approx*0.0)

5 RMSE

Next we run a training loop and plot the RMSE.

trn_iterations: int = 30
data_gen: Iterator[DataSeq] = example_model_data_generator()
tst_data: DataSeq = list(next(data_gen))
tabular: Tabular[Triple] = Tabular()
rmses = []
for xy_seq in itertools.islice(data_gen, trn_iterations):
    tabular = tabular.update(xy_seq)
    rmse: float = tabular.rmse(tst_data)
    rmses.append(rmse)
    print(f"RMSE: {rmse:.2f}")
RMSE: 2.83
RMSE: 2.45
RMSE: 2.31
RMSE: 2.24
RMSE: 2.19
RMSE: 2.16
RMSE: 2.13
RMSE: 2.12
RMSE: 2.11
RMSE: 2.10
RMSE: 2.09
RMSE: 2.08
RMSE: 2.08
RMSE: 2.07
RMSE: 2.07
RMSE: 2.06
RMSE: 2.06
RMSE: 2.05
RMSE: 2.05
RMSE: 2.05
RMSE: 2.05
RMSE: 2.04
RMSE: 2.04
RMSE: 2.04
RMSE: 2.04
RMSE: 2.04
RMSE: 2.03
RMSE: 2.03
RMSE: 2.03
RMSE: 2.03
import matplotlib.pyplot as plt
fig,axs = plt.subplots(figsize=(13,10))
axs.set_xlabel('Iterations', fontsize=20)
axs.set_title(f'Tabular: RMSE', fontsize=24)
axs.plot(rmses, linewidth=3.0, color='green')
axs.legend(fontsize=20);
WARNING:matplotlib.legend:No handles with labels found to put in legend.