!python --versionPython 3.7.15Introduction to Function Approximation
Kobus Esterhuysen
July 13, 2022
When the state space becomes very large it is not feasible or even possible to make use of a tabular representation for a MDP (Markov Decision Process). Assume we have access to data in the form of a sequence of
We can now attempt to estimate the probability density of
The model-expected value of
Some terminology:
We are laying the groundwork for the development of software for Approximate Dynamic Programming as well as Reinforcement Learning. In this context
We make use of the approach followed in http://web.stanford.edu/class/cme241/.
from __future__ import annotations
from typing import (Callable, Dict, Generic, Iterator, Iterable, List,
Mapping, Optional, Sequence, Tuple, TypeVar, overload)
from scipy.stats import norm
import numpy as np
from abc import ABC, abstractmethod
from collections import defaultdict
from dataclasses import dataclass, replace, field
import itertoolsLet’s setup a Data Model:
def example_model_data_generator() -> Iterator[Tuple[Triple, float]]:
coeffs: Aug_Triple = (1., 7., -2., 8.)
d = norm(loc=0., scale=0.3) #. normal distribution
while True:
pt: np.ndarray = np.random.randn(3)
x_val: Triple = (pt[0], pt[1], pt[2])
y_val: float = coeffs[0] + np.dot(coeffs[1:], pt) + \
d.rvs(size=1)[0]
yield (x_val, y_val)<generator object example_model_data_generator at 0x7f229409e050>Here are two ways to generate a specific number of data points:
[((-1.676290585013634, -0.20330675764064765, 1.2409198966103707),
-0.21621778064248845),
((0.8904228844005586, -1.0571951299100364, -1.3494027985154795),
-1.4489959017682092),
((-0.08739558879596565, -0.6113476539743781, -0.7888914401285738),
-4.6533727569600245),
((0.5708696624914378, -0.08369486644635994, -0.4633710969742489),
1.7281828649292816),
((0.35765591694879084, 1.5036560666530643, 1.5036581693073041),
12.660202897065746)][((1.0085819743173652, -1.268842630676064, -1.4728299417090938),
-1.0929519721173804),
((0.15991749003209738, 0.7827078239138043, -0.23670087664912695),
-0.8322309073547126),
((-0.03626491676513139, -0.22962172359834823, -0.16924944879064824),
0.18957400851337064),
((-0.6166727432386784, -0.7364383180552759, -0.3245738309763991),
-3.798426645143519),
((-0.4391577407965104, -0.00453671521783716, 0.5744307739264344),
2.7594997387666362)]Now we wrap this generator in an iterator that returns a specified number of
Configure it to generate train data:
trn_num_pts: int = 10_000
trn_data_gen: Iterator[DataSeq] = data_seq_generator(
data_generator=data_gen,
num_pts=trn_num_pts
)
trn_data_gen<generator object data_seq_generator at 0x7f2294105550>[((1.5141116022641963, 0.26998740175974173, -0.8685503731379335),
4.089701120386119),
((1.0820407355967383, 0.3427549775851617, 1.1078679073305953),
16.953635131550595),
((1.3241105796410801, 0.4075553673033938, -0.3144729996416032),
7.088605383221274),
((-0.1839293455432471, -0.7972913552060831, -0.2851165267014572),
-1.075779837694524),
((-0.675285392797429, -0.2880798686047421, 0.031245908101714626),
-2.553426109315997)]Configure it to generate test data:
tst_num_pts: int = 1_000
tst_data_gen: Iterator[DataSeq] = data_seq_generator(
data_generator=data_gen,
num_pts=tst_num_pts
)
tst_data_gen<generator object data_seq_generator at 0x7f2293e02050>[((-0.10523271957547835, -2.170589448784764, 0.3010749843788246),
7.277767867698341),
((-0.9983512260844962, 0.2934685812942415, -0.3282888943142292),
-9.20126365132198),
((0.4995019622616231, -1.0578397350955713, 1.546176654939797),
19.57345833833039),
((-0.10804134248084613, 1.1247507613502794, 0.9118420560826367),
5.368526961464931),
((0.3780358510623769, -1.6538367411196908, -1.2552602675932416),
-3.3073160186043435)]We define the next class to implement the function approximation X to allow for arbitrary data types
X = TypeVar('X') #. for arbitrary data types scriptX
F = TypeVar('F', bound='FunctionApprox')
SMALL_NUM = 1e-6
class FunctionApprox(ABC, Generic[X]):
@abstractmethod
def __add__(self: F, other: F) -> F:
pass
@abstractmethod
def __mul__(self: F, scalar: float) -> F:
pass
@abstractmethod
def objective_gradient(
self: F,
xy_vals_seq: Iterable[Tuple[X, float]],
obj_deriv_out_fun: Callable[[Sequence[X], Sequence[float]], np.ndarray]
) -> Gradient[F]:
pass
@abstractmethod
def evaluate(self, x_values_seq: Iterable[X]) -> np.ndarray:
pass
def __call__(self, x_value: X) -> float:
return self.evaluate([x_value]).item()
@abstractmethod
def update_with_gradient(
self: F,
gradient: Gradient[F]
) -> F:
pass
def update(
self: F,
xy_vals_seq: Iterable[Tuple[X, float]]
) -> F:
def deriv_func(x: Sequence[X], y: Sequence[float]) -> np.ndarray:
return self.evaluate(x) - np.array(y)
return self.update_with_gradient(
self.objective_gradient(xy_vals_seq, deriv_func)
)
@abstractmethod
def solve(
self: F,
xy_vals_seq: Iterable[Tuple[X, float]],
error_tolerance: Optional[float] = None
) -> F:
pass
@abstractmethod
def within(self: F, other: F, tolerance: float) -> bool:
pass
def iterate_updates(
self: F,
xy_seq_stream: Iterator[Iterable[Tuple[X, float]]]
) -> Iterator[F]:
return iterate.accumulate(
xy_seq_stream,
lambda fa, xy: fa.update(xy),
initial=self
)
def rmse(
self,
xy_vals_seq: Iterable[Tuple[X, float]]
) -> float:
x_seq, y_seq = zip(*xy_vals_seq)
errors: np.ndarray = self.evaluate(x_seq) - np.array(y_seq)
return np.sqrt(np.mean(errors * errors))
def argmax(self, xs: Iterable[X]) -> X:
args: Sequence[X] = list(xs)
return args[np.argmax(self.evaluate(args))]The most important methods are:
solve
xy_vals_seq: Iterable[Tuple[X, float]]error_tolerance: Optional[float]=NoneF
FunctionApprox update
xy_vals_seq: Iterable[Tuple[X, float]]
F
FunctionApprox evaluate
x_values_seq: Iterable[X]The following two methods provide support to the update method: - objective_gradient - Computes the gradient of an objective function of the self FunctionApprox with respect to the parameters in the internal representation of the FunctionApprox - The gradient is output in the form of a Gradient[FunctionApprox] whose internal parameters are equal to the gradient values - inputs - xy_vals_seq: Iterable[Tuple[X, float]] - obj_deriv_out_fun: Callable[[Sequence[X], Sequence[float]], np.ndarray] - the derivative of the objective with respect to the output (evaluate) of the FunctionApprox, when evaluated at a Sequence of x values and a Sequence of y values (to be obtained from xy_vals_seq) - output - Gradient[F] - update_with_gradient - Update the internal parameters of self FunctionApprox - inputs - gradient: Gradient[F] - output - F
The following methods are useful for derived classes of FunctionApprox:
iterate_updates
update method), with each internal parameter update done for each data set of (x,y) pairs in the input stream of xy_seq_streamxy_seq_stream: Iterator[Iterable[Tuple[X, float]]]Iterator[F]rmse
FunctionApprox’s predictions (from evaluate) and the associated xy_vals_seq: Iterable[Tuple[X, float]]float which is the RMSEargmax
X that maximizes the function being approximated.X
The Gradient class holds the FunctionApprox F:
@dataclass(frozen=True)
class Gradient(Generic[F]):
function_approx: F
@overload
def __add__(self, x: Gradient[F]) -> Gradient[F]:
...
@overload
def __add__(self, x: F) -> F:
...
def __add__(self, x):
if isinstance(x, Gradient):
return Gradient(self.function_approx + x.function_approx)
return self.function_approx + x
def __mul__(self: Gradient[F], x: float) -> Gradient[F]:
return Gradient(self.function_approx*x)
def zero(self) -> Gradient[F]:
return Gradient(self.function_approx*0.0)We need to transform a measurement of the state into a sequence of features
We also define a sequence of feature functions
We will treat
This leads to
Given that we have a sequence of data points
Similarly, we define the regularized cross-entropy loss function as
using
The gradient of
The update to the weights vector will be
where the gradient estimate
with
Next we implement the classes AdamGradient and Weights.
@dataclass(frozen=True)
class Weights:
adam_gradient: AdamGradient #. ADAM parameters
time: int #. how many times the weights have been updated
weights: np.ndarray #. weight parameters of the function approximation
adam_cache1: np.ndarray
adam_cache2: np.ndarray
@staticmethod
def create(
weights: np.ndarray,
adam_gradient: AdamGradient = AdamGradient.default_settings(),
adam_cache1: Optional[np.ndarray] = None,
adam_cache2: Optional[np.ndarray] = None
) -> Weights:
return Weights(
adam_gradient=adam_gradient,
time=0,
weights=weights,
adam_cache1=np.zeros_like(
weights
) if adam_cache1 is None else adam_cache1,
adam_cache2=np.zeros_like(
weights
) if adam_cache2 is None else adam_cache2
)
def update(self, gradient: np.ndarray) -> Weights:
time: int = self.time + 1
new_adam_cache1: np.ndarray = self.adam_gradient.decay1* \
self.adam_cache1 + (1 - self.adam_gradient.decay1)* gradient
new_adam_cache2: np.ndarray = self.adam_gradient.decay2* \
self.adam_cache2 + (1 - self.adam_gradient.decay2)*gradient**2
corrected_m: np.ndarray = new_adam_cache1 / \
(1 - self.adam_gradient.decay1**time)
corrected_v: np.ndarray = new_adam_cache2 / \
(1 - self.adam_gradient.decay2**time)
new_weights: np.ndarray = self.weights - \
self.adam_gradient.learning_rate*corrected_m / \
(np.sqrt(corrected_v) + SMALL_NUM)
return replace(
self,
time=time,
weights=new_weights,
adam_cache1=new_adam_cache1,
adam_cache2=new_adam_cache2,
)
def within(self, other: Weights, tolerance: float) -> bool:
return np.all(np.abs(self.weights - other.weights) <= tolerance).item()Now we are ready to implement the LinearFunctionApprox class:
@dataclass(frozen=True)
class LinearFunctionApprox(FunctionApprox[X]):
feature_functions: Sequence[Callable[[X], float]]
regularization_coeff: float
weights: Weights
direct_solve: bool
@staticmethod
def create( #. factory method
feature_functions: Sequence[Callable[[X], float]],
adam_gradient: AdamGradient = AdamGradient.default_settings(),
regularization_coeff: float = 0.,
weights: Optional[Weights] = None,
direct_solve: bool = True
) -> LinearFunctionApprox[X]:
return LinearFunctionApprox(
feature_functions=feature_functions,
regularization_coeff=regularization_coeff,
weights=Weights.create(
adam_gradient=adam_gradient,
weights=np.zeros(len(feature_functions))
) if weights is None else weights,
direct_solve=direct_solve
)
def get_feature_values(self, x_values_seq: Iterable[X]) -> np.ndarray:
return np.array(
[[f(x) for f in self.feature_functions] for x in x_values_seq]
)
def objective_gradient(
self,
xy_vals_seq: Iterable[Tuple[X, float]],
obj_deriv_out_fun: Callable[[Sequence[X], Sequence[float]], float]
) -> Gradient[LinearFunctionApprox[X]]:
x_vals, y_vals = zip(*xy_vals_seq)
obj_deriv_out: np.ndarray = obj_deriv_out_fun(x_vals, y_vals)
features: np.ndarray = self.get_feature_values(x_vals)
gradient: np.ndarray = \
features.T.dot(obj_deriv_out) / len(obj_deriv_out) \
+ self.regularization_coeff * self.weights.weights
return Gradient(replace(
self,
weights=replace(
self.weights,
weights=gradient
)
))
def __add__(self, other: LinearFunctionApprox[X]) -> \
LinearFunctionApprox[X]:
return replace(
self,
weights=replace(
self.weights,
weights=self.weights.weights + other.weights.weights
)
)
def __mul__(self, scalar: float) -> LinearFunctionApprox[X]:
return replace(
self,
weights=replace(
self.weights,
weights=self.weights.weights * scalar
)
)
def evaluate(self, x_values_seq: Iterable[X]) -> np.ndarray:
return np.dot(
self.get_feature_values(x_values_seq),
self.weights.weights
)
def update_with_gradient(
self,
gradient: Gradient[LinearFunctionApprox[X]]
) -> LinearFunctionApprox[X]:
return replace(
self,
weights=self.weights.update(
gradient.function_approx.weights.weights
)
)
def solve(
self,
xy_vals_seq: Iterable[Tuple[X, float]],
error_tolerance: Optional[float] = None
) -> LinearFunctionApprox[X]:
if self.direct_solve:
x_vals, y_vals = zip(*xy_vals_seq)
feature_vals: np.ndarray = self.get_feature_values(x_vals)
feature_vals_T: np.ndarray = feature_vals.T
left: np.ndarray = np.dot(feature_vals_T, feature_vals) \
+ feature_vals.shape[0] * self.regularization_coeff * \
np.eye(len(self.weights.weights))
right: np.ndarray = np.dot(feature_vals_T, y_vals)
ret = replace(
self,
weights=Weights.create(
adam_gradient=self.weights.adam_gradient,
weights=np.linalg.solve(left, right)
)
)
else:
tol: float = 1e-6 if error_tolerance is None else error_tolerance
def done(
a: LinearFunctionApprox[X],
b: LinearFunctionApprox[X],
tol: float = tol
) -> bool:
return a.within(b, tol)
ret = iterate.converged(
self.iterate_updates(itertools.repeat(list(xy_vals_seq))),
done=done
)
return ret
def within(self, other: FunctionApprox[X], tolerance: float) -> bool:
if isinstance(other, LinearFunctionApprox):
return self.weights.within(other.weights, tolerance)
return FalseSome of the methods are:
get_feature_values
x_values_seq: Iterable[X]np.ndarray
evaluate
x_values_seq: Iterable[X]np.ndarrayobjective_gradient
xy_vals_seq: Iterable[Tuple[X, float]]obj_deriv_out_fun: Callable[[Sequence[X], Sequence[float]], float]Gradient[LinearFunctionApprox[X]]update_with_gradient
gradient: Gradient[LinearFunctionApprox[X]]LinearFunctionApprox[X]solve
xy_vals_seq: Iterable[Tuple[X, float]]error_tolerance: Optional[float]=NoneLinearFunctionApprox[X]Next we write a function to create a LinearFunctionApprox.
[<function __main__.feature_functions.<locals>.<lambda>(_)>,
<function __main__.feature_functions.<locals>.<lambda>(x)>,
<function __main__.feature_functions.<locals>.<lambda>(x)>,
<function __main__.feature_functions.<locals>.<lambda>(x)>]Next, we will generalize the linear function approximation so that we can have non-linear functions. For this we use a simple deep neural network. It will be of the feed-forward, fully-connected type. A neural network consists of
Additionally, - vector
Some conventions on linear algebra: - all vectors treated as column vectors - gradient of a vector of dimension
The calculation provided by a neural network to transform a predictor variable
This calculation will be implemented by means of the evaluate method below.
Next we want an expression for the cross-entropy loss gradient with respect to the parameters for each of the layers, i.e.
where the symbol
Adding
The following class captures the architecture of an implemented neural network.
@dataclass(frozen=True)
class DNNSpec:
neurons: Sequence[int]
bias: bool
hidden_activation: Callable[[np.ndarray], np.ndarray]
hidden_activation_deriv: Callable[[np.ndarray], np.ndarray]
output_activation: Callable[[np.ndarray], np.ndarray]
output_activation_deriv: Callable[[np.ndarray], np.ndarray]neurons
bias
bias is True:
hidden_activation np.array to np.array
hidden_activation_deriv np.array to np.array
output_activation np.array to np.array
output_activation_deriv np.array to np.array
The next class implements the Deep Neural Network Approximation:
@dataclass(frozen=True)
class DNNApprox(FunctionApprox[X]):
feature_functions: Sequence[Callable[[X], float]]
dnn_spec: DNNSpec
regularization_coeff: float
weights: Sequence[Weights]
@staticmethod
def create( #. factory method
feature_functions: Sequence[Callable[[X], float]],
dnn_spec: DNNSpec,
adam_gradient: AdamGradient = AdamGradient.default_settings(),
regularization_coeff: float = 0.,
weights: Optional[Sequence[Weights]] = None
) -> DNNApprox[X]:
if weights is None:
inputs: Sequence[int] = [len(feature_functions)] + \
[n + (1 if dnn_spec.bias else 0)
for i, n in enumerate(dnn_spec.neurons)]
outputs: Sequence[int] = list(dnn_spec.neurons) + [1]
wts = [Weights.create(
weights=np.random.randn(output, inp)/np.sqrt(inp),
adam_gradient=adam_gradient
) for inp, output in zip(inputs, outputs)]
else:
wts = weights
return DNNApprox(
feature_functions=feature_functions,
dnn_spec=dnn_spec,
regularization_coeff=regularization_coeff,
weights=wts
)
def get_feature_values(self, x_values_seq: Iterable[X]) -> np.ndarray:
return np.array(
[[f(x) for f in self.feature_functions] for x in x_values_seq]
)
def forward_propagation(
self,
x_values_seq: Iterable[X]
) -> Sequence[np.ndarray]:
inp: np.ndarray = self.get_feature_values(x_values_seq)
ret: List[np.ndarray] = [inp]
for w in self.weights[:-1]:
out: np.ndarray = self.dnn_spec.hidden_activation(
np.dot(inp, w.weights.T)
)
if self.dnn_spec.bias:
inp = np.insert(out, 0, 1., axis=1)
else:
inp = out
ret.append(inp)
ret.append(
self.dnn_spec.output_activation(
np.dot(inp, self.weights[-1].weights.T)
)[:, 0]
)
return ret
def evaluate(self, x_values_seq: Iterable[X]) -> np.ndarray:
return self.forward_propagation(x_values_seq)[-1]
def backward_propagation(
self,
fwd_prop: Sequence[np.ndarray],
obj_deriv_out: np.ndarray
) -> Sequence[np.ndarray]:
deriv: np.ndarray = obj_deriv_out.reshape(1, -1)
back_prop: List[np.ndarray] = [np.dot(deriv, fwd_prop[-1]) /
deriv.shape[1]]
for i in reversed(range(len(self.weights) - 1)):
deriv = np.dot(self.weights[i + 1].weights.T, deriv) * \
self.dnn_spec.hidden_activation_deriv(fwd_prop[i + 1].T)
if self.dnn_spec.bias:
deriv = deriv[1:]
back_prop.append(np.dot(deriv, fwd_prop[i]) / deriv.shape[1])
return back_prop[::-1]
def objective_gradient(
self,
xy_vals_seq: Iterable[Tuple[X, float]],
obj_deriv_out_fun: Callable[[Sequence[X], Sequence[float]], float]
) -> Gradient[DNNApprox[X]]:
x_vals, y_vals = zip(*xy_vals_seq)
obj_deriv_out: np.ndarray = obj_deriv_out_fun(x_vals, y_vals)
fwd_prop: Sequence[np.ndarray] = self.forward_propagation(x_vals)[:-1]
gradient: Sequence[np.ndarray] = \
[x + self.regularization_coeff * self.weights[i].weights
for i, x in enumerate(self.backward_propagation(
fwd_prop=fwd_prop,
obj_deriv_out=obj_deriv_out
))]
return Gradient(replace(
self,
weights=[replace(w, weights=g) for
w, g in zip(self.weights, gradient)]
))
def __add__(self, other: DNNApprox[X]) -> DNNApprox[X]:
return replace(
self,
weights=[replace(w, weights=w.weights + o.weights) for
w, o in zip(self.weights, other.weights)]
)
def __mul__(self, scalar: float) -> DNNApprox[X]:
return replace(
self,
weights=[replace(w, weights=w.weights * scalar)
for w in self.weights]
)
def update_with_gradient(
self,
gradient: Gradient[DNNApprox[X]]
) -> DNNApprox[X]:
return replace(
self,
weights=[w.update(g.weights) for w, g in
zip(self.weights, gradient.function_approx.weights)]
)
def solve(
self,
xy_vals_seq: Iterable[Tuple[X, float]],
error_tolerance: Optional[float] = None
) -> DNNApprox[X]:
tol: float = 1e-6 if error_tolerance is None else error_tolerance
def done(
a: DNNApprox[X],
b: DNNApprox[X],
tol: float = tol
) -> bool:
return a.within(b, tol)
return iterate.converged(
self.iterate_updates(itertools.repeat(list(xy_vals_seq))),
done=done
)
def within(self, other: FunctionApprox[X], tolerance: float) -> bool:
if isinstance(other, DNNApprox):
return all(w1.within(w2, tolerance)
for w1, w2 in zip(self.weights, other.weights))
else:
return Falsefeature_functions: Sequence[Callable[[X], float]]
dnn_spec: DNNSpecregularization_coeff: float
weights: Sequence[Weights]
get_feature_values
x_values_seq: Iterable[X]np.ndarray
forward_propagation
x_values_seq: Iterable[X]
Sequence[np.ndarray]evaluate
x_values_seq: Iterable[X]
np.ndarrayforward_propagation (backward_propagation
fwd_prop: Sequence[np.ndarray]
obj_deriv_out: np.ndarray
Sequence[np.ndarray]
objective_gradient
xy_vals_seq: Iterable[Tuple[X, float]]obj_deriv_out_fun: Callable[[Sequence[X], Sequence[float]], float]update_with_gradient
gradient: Gradient[DNNApprox[X]]DNNApprox[X]solve
xy_vals_seq: Iterable[Tuple[X, float]]error_tolerance: Optional[float]=NoneDNNApprox[X]iterate_updates and within to perform a best-fit of the weights Next we write a function to create a DNNApprox with 1 hidden layer having 2 neurons. We also add some regularization.
def get_dnn_model() -> DNNApprox[Triple]:
ffs = feature_functions()
ag = adam_gradient()
def relu(arg: np.ndarray) -> np.ndarray:
return np.vectorize(lambda x: x if x > 0. else 0.)(arg)
def relu_deriv(res: np.ndarray) -> np.ndarray:
return np.vectorize(lambda x: 1. if x > 0. else 0.)(res)
def identity(arg: np.ndarray) -> np.ndarray:
return arg
def identity_deriv(res: np.ndarray) -> np.ndarray:
return np.ones_like(res)
ds = DNNSpec(
neurons=[2],
bias=True,
hidden_activation=relu,
hidden_activation_deriv=relu_deriv,
output_activation=identity,
output_activation_deriv=identity_deriv
)
return DNNApprox.create(
feature_functions=ffs,
dnn_spec=ds,
adam_gradient=ag,
regularization_coeff=0.05
)DNNApprox(feature_functions=[<function feature_functions.<locals>.<lambda> at 0x7f22a03227a0>, <function feature_functions.<locals>.<lambda> at 0x7f22a0322e60>, <function feature_functions.<locals>.<lambda> at 0x7f22a0322560>, <function feature_functions.<locals>.<lambda> at 0x7f22a0322440>], dnn_spec=DNNSpec(neurons=[2], bias=True, hidden_activation=<function get_dnn_model.<locals>.relu at 0x7f22a0322050>, hidden_activation_deriv=<function get_dnn_model.<locals>.relu_deriv at 0x7f22a0322c20>, output_activation=<function get_dnn_model.<locals>.identity at 0x7f22a0322dd0>, output_activation_deriv=<function get_dnn_model.<locals>.identity_deriv at 0x7f22a0322d40>), regularization_coeff=0.05, weights=[Weights(adam_gradient=AdamGradient(learning_rate=0.1, decay1=0.9, decay2=0.999), time=0, weights=array([[ 0.1933681 , 0.38027881, -0.00492979, -0.76650108],
[-0.10652202, -0.0332175 , -0.17239005, 0.89441099]]), adam_cache1=array([[0., 0., 0., 0.],
[0., 0., 0., 0.]]), adam_cache2=array([[0., 0., 0., 0.],
[0., 0., 0., 0.]])), Weights(adam_gradient=AdamGradient(learning_rate=0.1, decay1=0.9, decay2=0.999), time=0, weights=array([[-0.69480787, -0.92598947, 0.12214709]]), adam_cache1=array([[0., 0., 0.]]), adam_cache2=array([[0., 0., 0.]]))])Next, we do a direct solve on a LinearFunctionApprox instance.
direct_solve_lfap: LinearFunctionApprox[Triple] = \
get_linear_model().solve(next(trn_data_gen))
direct_solve_rmse: float = direct_solve_lfap.rmse(tst_data)
print(f"Linear Model Direct Solve RMSE = {direct_solve_rmse:.3f}")
print("-----------------------------")Linear Model Direct Solve RMSE = 0.302
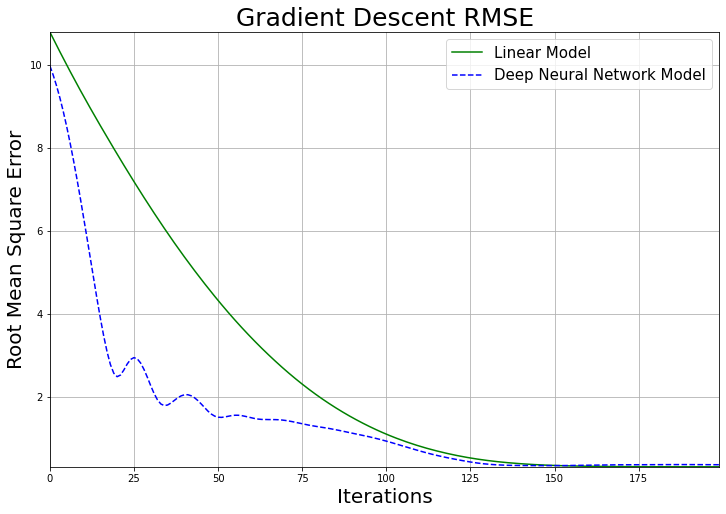
-----------------------------Next we want to do SGD (Stochastic Gradient Descent) with each of the two function approximations so that we can compare how their RMSE (Root-Mean-Square-Errors) decline with the number of iterations.
print("Linear Model SGD")
print("----------------")
lfap_rmse_seq: List[float] = []
lfap_weights_seq: List[Weights] = [] #.
for lfap in itertools.islice(
get_linear_model().iterate_updates(trn_data_gen),
trn_iterations
):
this_rmse: float = lfap.rmse(tst_data)
lfap_rmse_seq.append(this_rmse)
lfap_weights_seq.append(lfap.weights) #.
iter: int = len(lfap_rmse_seq)
print(f"Iteration {iter:d}: RMSE = {this_rmse:.3f}")Linear Model SGD
----------------
Iteration 1: RMSE = 10.803
Iteration 2: RMSE = 10.641
Iteration 3: RMSE = 10.481
Iteration 4: RMSE = 10.322
Iteration 5: RMSE = 10.164
Iteration 6: RMSE = 10.008
Iteration 7: RMSE = 9.854
Iteration 8: RMSE = 9.702
Iteration 9: RMSE = 9.552
Iteration 10: RMSE = 9.403
Iteration 11: RMSE = 9.256
Iteration 12: RMSE = 9.110
Iteration 13: RMSE = 8.966
Iteration 14: RMSE = 8.824
Iteration 15: RMSE = 8.682
Iteration 16: RMSE = 8.542
Iteration 17: RMSE = 8.403
Iteration 18: RMSE = 8.264
Iteration 19: RMSE = 8.127
Iteration 20: RMSE = 7.990
Iteration 21: RMSE = 7.854
Iteration 22: RMSE = 7.719
Iteration 23: RMSE = 7.586
Iteration 24: RMSE = 7.452
Iteration 25: RMSE = 7.320
Iteration 26: RMSE = 7.190
Iteration 27: RMSE = 7.060
Iteration 28: RMSE = 6.931
Iteration 29: RMSE = 6.804
Iteration 30: RMSE = 6.677
Iteration 31: RMSE = 6.552
Iteration 32: RMSE = 6.428
Iteration 33: RMSE = 6.306
Iteration 34: RMSE = 6.184
Iteration 35: RMSE = 6.064
Iteration 36: RMSE = 5.945
Iteration 37: RMSE = 5.827
Iteration 38: RMSE = 5.711
Iteration 39: RMSE = 5.596
Iteration 40: RMSE = 5.482
Iteration 41: RMSE = 5.370
Iteration 42: RMSE = 5.260
Iteration 43: RMSE = 5.150
Iteration 44: RMSE = 5.042
Iteration 45: RMSE = 4.935
Iteration 46: RMSE = 4.829
Iteration 47: RMSE = 4.725
Iteration 48: RMSE = 4.622
Iteration 49: RMSE = 4.520
Iteration 50: RMSE = 4.420
Iteration 51: RMSE = 4.321
Iteration 52: RMSE = 4.223
Iteration 53: RMSE = 4.127
Iteration 54: RMSE = 4.032
Iteration 55: RMSE = 3.939
Iteration 56: RMSE = 3.847
Iteration 57: RMSE = 3.757
Iteration 58: RMSE = 3.668
Iteration 59: RMSE = 3.581
Iteration 60: RMSE = 3.495
Iteration 61: RMSE = 3.410
Iteration 62: RMSE = 3.327
Iteration 63: RMSE = 3.245
Iteration 64: RMSE = 3.164
Iteration 65: RMSE = 3.085
Iteration 66: RMSE = 3.007
Iteration 67: RMSE = 2.930
Iteration 68: RMSE = 2.855
Iteration 69: RMSE = 2.781
Iteration 70: RMSE = 2.708
Iteration 71: RMSE = 2.636
Iteration 72: RMSE = 2.566
Iteration 73: RMSE = 2.498
Iteration 74: RMSE = 2.430
Iteration 75: RMSE = 2.364
Iteration 76: RMSE = 2.300
Iteration 77: RMSE = 2.236
Iteration 78: RMSE = 2.174
Iteration 79: RMSE = 2.114
Iteration 80: RMSE = 2.055
Iteration 81: RMSE = 1.997
Iteration 82: RMSE = 1.940
Iteration 83: RMSE = 1.885
Iteration 84: RMSE = 1.831
Iteration 85: RMSE = 1.778
Iteration 86: RMSE = 1.726
Iteration 87: RMSE = 1.676
Iteration 88: RMSE = 1.627
Iteration 89: RMSE = 1.579
Iteration 90: RMSE = 1.532
Iteration 91: RMSE = 1.487
Iteration 92: RMSE = 1.443
Iteration 93: RMSE = 1.399
Iteration 94: RMSE = 1.357
Iteration 95: RMSE = 1.316
Iteration 96: RMSE = 1.276
Iteration 97: RMSE = 1.237
Iteration 98: RMSE = 1.199
Iteration 99: RMSE = 1.162
Iteration 100: RMSE = 1.126
Iteration 101: RMSE = 1.091
Iteration 102: RMSE = 1.058
Iteration 103: RMSE = 1.025
Iteration 104: RMSE = 0.993
Iteration 105: RMSE = 0.963
Iteration 106: RMSE = 0.933
Iteration 107: RMSE = 0.904
Iteration 108: RMSE = 0.877
Iteration 109: RMSE = 0.850
Iteration 110: RMSE = 0.824
Iteration 111: RMSE = 0.799
Iteration 112: RMSE = 0.774
Iteration 113: RMSE = 0.751
Iteration 114: RMSE = 0.729
Iteration 115: RMSE = 0.707
Iteration 116: RMSE = 0.686
Iteration 117: RMSE = 0.666
Iteration 118: RMSE = 0.646
Iteration 119: RMSE = 0.628
Iteration 120: RMSE = 0.609
Iteration 121: RMSE = 0.592
Iteration 122: RMSE = 0.575
Iteration 123: RMSE = 0.559
Iteration 124: RMSE = 0.544
Iteration 125: RMSE = 0.530
Iteration 126: RMSE = 0.516
Iteration 127: RMSE = 0.503
Iteration 128: RMSE = 0.490
Iteration 129: RMSE = 0.478
Iteration 130: RMSE = 0.467
Iteration 131: RMSE = 0.456
Iteration 132: RMSE = 0.446
Iteration 133: RMSE = 0.436
Iteration 134: RMSE = 0.427
Iteration 135: RMSE = 0.419
Iteration 136: RMSE = 0.411
Iteration 137: RMSE = 0.403
Iteration 138: RMSE = 0.396
Iteration 139: RMSE = 0.389
Iteration 140: RMSE = 0.383
Iteration 141: RMSE = 0.377
Iteration 142: RMSE = 0.372
Iteration 143: RMSE = 0.366
Iteration 144: RMSE = 0.361
Iteration 145: RMSE = 0.357
Iteration 146: RMSE = 0.353
Iteration 147: RMSE = 0.349
Iteration 148: RMSE = 0.345
Iteration 149: RMSE = 0.341
Iteration 150: RMSE = 0.338
Iteration 151: RMSE = 0.335
Iteration 152: RMSE = 0.332
Iteration 153: RMSE = 0.330
Iteration 154: RMSE = 0.328
Iteration 155: RMSE = 0.326
Iteration 156: RMSE = 0.324
Iteration 157: RMSE = 0.322
Iteration 158: RMSE = 0.320
Iteration 159: RMSE = 0.319
Iteration 160: RMSE = 0.317
Iteration 161: RMSE = 0.316
Iteration 162: RMSE = 0.315
Iteration 163: RMSE = 0.314
Iteration 164: RMSE = 0.313
Iteration 165: RMSE = 0.312
Iteration 166: RMSE = 0.311
Iteration 167: RMSE = 0.310
Iteration 168: RMSE = 0.309
Iteration 169: RMSE = 0.309
Iteration 170: RMSE = 0.308
Iteration 171: RMSE = 0.308
Iteration 172: RMSE = 0.307
Iteration 173: RMSE = 0.307
Iteration 174: RMSE = 0.306
Iteration 175: RMSE = 0.306
Iteration 176: RMSE = 0.305
Iteration 177: RMSE = 0.305
Iteration 178: RMSE = 0.305
Iteration 179: RMSE = 0.305
Iteration 180: RMSE = 0.304
Iteration 181: RMSE = 0.304
Iteration 182: RMSE = 0.304
Iteration 183: RMSE = 0.304
Iteration 184: RMSE = 0.304
Iteration 185: RMSE = 0.304
Iteration 186: RMSE = 0.304
Iteration 187: RMSE = 0.304
Iteration 188: RMSE = 0.304
Iteration 189: RMSE = 0.304
Iteration 190: RMSE = 0.303
Iteration 191: RMSE = 0.303
Iteration 192: RMSE = 0.303
Iteration 193: RMSE = 0.303
Iteration 194: RMSE = 0.303
Iteration 195: RMSE = 0.303
Iteration 196: RMSE = 0.303
Iteration 197: RMSE = 0.303
Iteration 198: RMSE = 0.303
Iteration 199: RMSE = 0.303
Iteration 200: RMSE = 0.303print("DNN Model SGD")
print("-------------")
dfap_rmse_seq: List[float] = []
dfap_weights_seq: List[Weights] = [] #.
for dfap in itertools.islice(
get_dnn_model().iterate_updates(trn_data_gen),
trn_iterations
):
this_rmse: float = dfap.rmse(tst_data)
dfap_rmse_seq.append(this_rmse)
dfap_weights_seq.append(dfap.weights) #.
iter: int = len(dfap_rmse_seq)
print(f"Iteration {iter:d}: RMSE = {this_rmse:.3f}")DNN Model SGD
-------------
Iteration 1: RMSE = 9.987
Iteration 2: RMSE = 9.761
Iteration 3: RMSE = 9.501
Iteration 4: RMSE = 9.208
Iteration 5: RMSE = 8.881
Iteration 6: RMSE = 8.522
Iteration 7: RMSE = 8.133
Iteration 8: RMSE = 7.718
Iteration 9: RMSE = 7.279
Iteration 10: RMSE = 6.820
Iteration 11: RMSE = 6.343
Iteration 12: RMSE = 5.853
Iteration 13: RMSE = 5.353
Iteration 14: RMSE = 4.855
Iteration 15: RMSE = 4.367
Iteration 16: RMSE = 3.900
Iteration 17: RMSE = 3.467
Iteration 18: RMSE = 3.085
Iteration 19: RMSE = 2.773
Iteration 20: RMSE = 2.563
Iteration 21: RMSE = 2.479
Iteration 22: RMSE = 2.518
Iteration 23: RMSE = 2.641
Iteration 24: RMSE = 2.785
Iteration 25: RMSE = 2.895
Iteration 26: RMSE = 2.939
Iteration 27: RMSE = 2.909
Iteration 28: RMSE = 2.807
Iteration 29: RMSE = 2.652
Iteration 30: RMSE = 2.462
Iteration 31: RMSE = 2.259
Iteration 32: RMSE = 2.070
Iteration 33: RMSE = 1.918
Iteration 34: RMSE = 1.820
Iteration 35: RMSE = 1.781
Iteration 36: RMSE = 1.795
Iteration 37: RMSE = 1.843
Iteration 38: RMSE = 1.906
Iteration 39: RMSE = 1.968
Iteration 40: RMSE = 2.015
Iteration 41: RMSE = 2.042
Iteration 42: RMSE = 2.044
Iteration 43: RMSE = 2.018
Iteration 44: RMSE = 1.971
Iteration 45: RMSE = 1.902
Iteration 46: RMSE = 1.820
Iteration 47: RMSE = 1.732
Iteration 48: RMSE = 1.647
Iteration 49: RMSE = 1.576
Iteration 50: RMSE = 1.527
Iteration 51: RMSE = 1.501
Iteration 52: RMSE = 1.496
Iteration 53: RMSE = 1.507
Iteration 54: RMSE = 1.524
Iteration 55: RMSE = 1.539
Iteration 56: RMSE = 1.548
Iteration 57: RMSE = 1.548
Iteration 58: RMSE = 1.539
Iteration 59: RMSE = 1.523
Iteration 60: RMSE = 1.503
Iteration 61: RMSE = 1.483
Iteration 62: RMSE = 1.467
Iteration 63: RMSE = 1.454
Iteration 64: RMSE = 1.447
Iteration 65: RMSE = 1.444
Iteration 66: RMSE = 1.444
Iteration 67: RMSE = 1.443
Iteration 68: RMSE = 1.442
Iteration 69: RMSE = 1.439
Iteration 70: RMSE = 1.432
Iteration 71: RMSE = 1.423
Iteration 72: RMSE = 1.410
Iteration 73: RMSE = 1.394
Iteration 74: RMSE = 1.377
Iteration 75: RMSE = 1.359
Iteration 76: RMSE = 1.342
Iteration 77: RMSE = 1.324
Iteration 78: RMSE = 1.309
Iteration 79: RMSE = 1.294
Iteration 80: RMSE = 1.281
Iteration 81: RMSE = 1.268
Iteration 82: RMSE = 1.256
Iteration 83: RMSE = 1.243
Iteration 84: RMSE = 1.229
Iteration 85: RMSE = 1.214
Iteration 86: RMSE = 1.198
Iteration 87: RMSE = 1.182
Iteration 88: RMSE = 1.165
Iteration 89: RMSE = 1.147
Iteration 90: RMSE = 1.130
Iteration 91: RMSE = 1.114
Iteration 92: RMSE = 1.097
Iteration 93: RMSE = 1.080
Iteration 94: RMSE = 1.063
Iteration 95: RMSE = 1.045
Iteration 96: RMSE = 1.026
Iteration 97: RMSE = 1.008
Iteration 98: RMSE = 0.988
Iteration 99: RMSE = 0.967
Iteration 100: RMSE = 0.946
Iteration 101: RMSE = 0.923
Iteration 102: RMSE = 0.900
Iteration 103: RMSE = 0.877
Iteration 104: RMSE = 0.853
Iteration 105: RMSE = 0.829
Iteration 106: RMSE = 0.804
Iteration 107: RMSE = 0.780
Iteration 108: RMSE = 0.755
Iteration 109: RMSE = 0.731
Iteration 110: RMSE = 0.707
Iteration 111: RMSE = 0.684
Iteration 112: RMSE = 0.661
Iteration 113: RMSE = 0.639
Iteration 114: RMSE = 0.618
Iteration 115: RMSE = 0.598
Iteration 116: RMSE = 0.579
Iteration 117: RMSE = 0.560
Iteration 118: RMSE = 0.542
Iteration 119: RMSE = 0.525
Iteration 120: RMSE = 0.508
Iteration 121: RMSE = 0.492
Iteration 122: RMSE = 0.477
Iteration 123: RMSE = 0.462
Iteration 124: RMSE = 0.447
Iteration 125: RMSE = 0.432
Iteration 126: RMSE = 0.419
Iteration 127: RMSE = 0.407
Iteration 128: RMSE = 0.395
Iteration 129: RMSE = 0.385
Iteration 130: RMSE = 0.376
Iteration 131: RMSE = 0.368
Iteration 132: RMSE = 0.361
Iteration 133: RMSE = 0.355
Iteration 134: RMSE = 0.350
Iteration 135: RMSE = 0.346
Iteration 136: RMSE = 0.342
Iteration 137: RMSE = 0.340
Iteration 138: RMSE = 0.338
Iteration 139: RMSE = 0.336
Iteration 140: RMSE = 0.335
Iteration 141: RMSE = 0.334
Iteration 142: RMSE = 0.333
Iteration 143: RMSE = 0.333
Iteration 144: RMSE = 0.332
Iteration 145: RMSE = 0.332
Iteration 146: RMSE = 0.332
Iteration 147: RMSE = 0.332
Iteration 148: RMSE = 0.331
Iteration 149: RMSE = 0.331
Iteration 150: RMSE = 0.331
Iteration 151: RMSE = 0.331
Iteration 152: RMSE = 0.332
Iteration 153: RMSE = 0.332
Iteration 154: RMSE = 0.333
Iteration 155: RMSE = 0.334
Iteration 156: RMSE = 0.335
Iteration 157: RMSE = 0.336
Iteration 158: RMSE = 0.337
Iteration 159: RMSE = 0.338
Iteration 160: RMSE = 0.340
Iteration 161: RMSE = 0.341
Iteration 162: RMSE = 0.343
Iteration 163: RMSE = 0.344
Iteration 164: RMSE = 0.345
Iteration 165: RMSE = 0.346
Iteration 166: RMSE = 0.348
Iteration 167: RMSE = 0.349
Iteration 168: RMSE = 0.350
Iteration 169: RMSE = 0.351
Iteration 170: RMSE = 0.351
Iteration 171: RMSE = 0.352
Iteration 172: RMSE = 0.352
Iteration 173: RMSE = 0.353
Iteration 174: RMSE = 0.353
Iteration 175: RMSE = 0.354
Iteration 176: RMSE = 0.355
Iteration 177: RMSE = 0.355
Iteration 178: RMSE = 0.355
Iteration 179: RMSE = 0.355
Iteration 180: RMSE = 0.355
Iteration 181: RMSE = 0.355
Iteration 182: RMSE = 0.356
Iteration 183: RMSE = 0.356
Iteration 184: RMSE = 0.356
Iteration 185: RMSE = 0.356
Iteration 186: RMSE = 0.356
Iteration 187: RMSE = 0.357
Iteration 188: RMSE = 0.357
Iteration 189: RMSE = 0.357
Iteration 190: RMSE = 0.357
Iteration 191: RMSE = 0.357
Iteration 192: RMSE = 0.357
Iteration 193: RMSE = 0.356
Iteration 194: RMSE = 0.356
Iteration 195: RMSE = 0.355
Iteration 196: RMSE = 0.354
Iteration 197: RMSE = 0.354
Iteration 198: RMSE = 0.354
Iteration 199: RMSE = 0.353
Iteration 200: RMSE = 0.353x_vals = range(trn_iterations)
plot_list_of_curves(
list_of_x_vals=[x_vals, x_vals],
list_of_y_vals=[lfap_rmse_seq, dfap_rmse_seq],
list_of_colors=["g-", "b--"],
list_of_curve_labels=["Linear Model", "Deep Neural Network Model"],
x_label="Iterations",
y_label="Root Mean Square Error",
title="Gradient Descent RMSE"
)
It will also be interesting to see how the weights converge during training.
import matplotlib.pyplot as plt
fig,axs = plt.subplots(figsize=(13,10))
axs.set_xlabel('Iterations', fontsize=20)
axs.set_title(f'LinearFunctionApprox: Convergence of weight values', fontsize=24)
for i in range(len(lfap_weights_lst)):
axs.plot(lfap_weights_lst[i], label=f'$\{weight_names[i]}$', linewidth=3.0)
axs.legend(fontsize=20);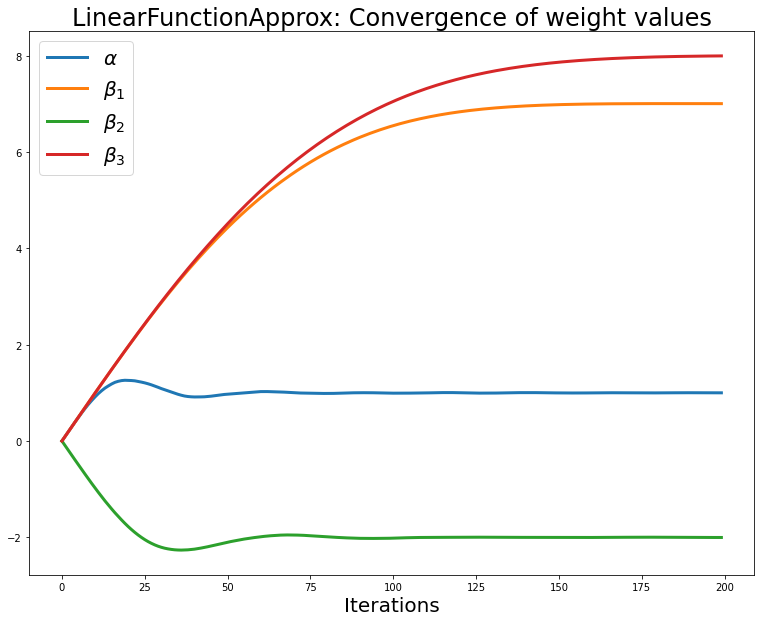
import matplotlib.pyplot as plt
fig,axs = plt.subplots(figsize=(13,10))
axs.set_xlabel('Iterations', fontsize=20)
axs.set_title(f'DNNApprox: Convergence of neuron 0 weight values', fontsize=24)
for i in range(len(dfap_weights_lst_0)):
axs.plot(dfap_weights_lst_0[i], label=f'$\{weight_names[i]}$', linewidth=3.0)
axs.legend(fontsize=20);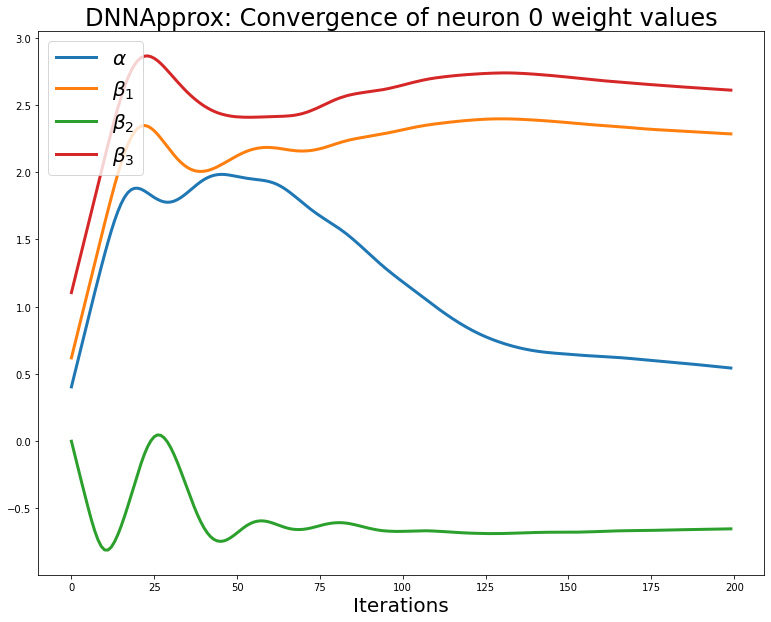
import matplotlib.pyplot as plt
fig,axs = plt.subplots(figsize=(13,10))
axs.set_xlabel('Iterations', fontsize=20)
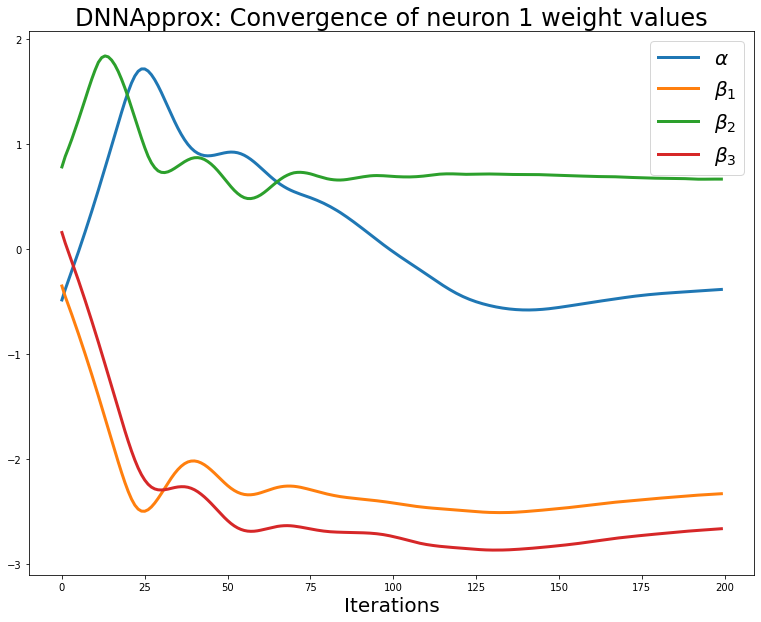
axs.set_title(f'DNNApprox: Convergence of neuron 1 weight values', fontsize=24)
for i in range(len(dfap_weights_lst_1)):
axs.plot(dfap_weights_lst_1[i], label=f'$\{weight_names[i]}$', linewidth=3.0)
axs.legend(fontsize=20);