An RL Approach for Inventory Management (Part 11)

Tabular Temporal-Difference (Q-Learning) Control

Inventory Management
Markov Decision Process
TD
QLearning
Author

Kobus Esterhuysen

Published

July 22, 2022

1 Generalized Policy Iteration (GPI)

In previous projects we have only dealt with the prediction problem. In this project we move on to the control problem. We stay in the model-free or learning domain (rather than planning), i.e. making use of Reinforcement Learning algorithms. We will explore the depth of update dimension, considering both bootstrapping and non-bootstrapping methods like Temporal-Difference (TD) and Monte-Carlo (MC) algorithms respectively.

What is different about Control, rather than Prediction, is the depence on the concept of Generalized Policy Iteration (GPI).

The key concept of GPI is that we can: - Evaluate a policy with any Policy Evaluation method - Improve a policy with any Policy Improvement method

2 Off-Policy Control

For all control algorithms there is a conflict between trying to learn Q-Values that associated with optimal behavior and the need to explore all actions. How do we address this?

  • Our approach so far (which is a hack)
    • pursue an \(\epsilon\)-greedy policy
    • almost optimal policy
  • Better, cleaner approach
    • Two policies, one for each competing interest
      • Target Policy \(\pi\)
        • the target of Control
        • learn about this policy
        • becomes optimal policy eventually
      • Behavior Policy \(\mu\)
        • behaves in an exploratory manner
        • allows for sufficient data for all actions
        • enables adequate estimate of the Q-Value Function
    • Known as off-policy algorithms
    • Allows for more general and more powerful RL slgorithms
    • Off-Policy algorithm
      • estimate the Value Function for target policy \(\pi\) while it
      • follows behavior policy \(\mu\)
    • Advantages of Off-Policy algorithms
      • can learn the target policy \(\pi\) by observing humans or other AI agents who follow a behavior policy \(\mu\)
      • can re-use prior experiences that were genrated from old policies, say \(\pi_1, \pi_2, ...\)

3 Q-Learning

To get to the Q-Learning algorithm we tweak the SARSA algorithm to make it Off-Policy.

First tweak: - Instead of generating - both action \(A\) and next action \(A'\) by the - same \(\epsilon\)-greedy policy - we generate - action \(A\) using (exploratory) behavior policy \(\mu\) - next action \(A'\) using target policy \(\pi\)

Second tweak: - Instead of advancing to the next time step by - setting \(S_{t+1}\) to \(S'_t\) and \(A_{t+1}\) to \(A'_t\) - we advance by - only setting \(S_{t+1}\) to \(S'_t\) while \(A_{t+1}\) is generated using the behavior policy \(\mu\)

!python --version
Python 3.7.15
from typing import Callable, Iterator, Tuple, Mapping
import itertools
import inspect
from pprint import pprint

4 Temporal-Difference (TD) Control (Q-Learning)

We need to ensure that the target policy eventually turns into the optimal policy. A straightforward way to do this is to have the target policy equal to the deterministic greedy policy derived from the Q-Value Function estimate at each step. This leads to the parameter update:

\[ \begin{aligned} \Delta w &= \alpha \cdot \delta_t \cdot \nabla_w Q(S_t,A_t;w) \end{aligned} \]

where

\[ \begin{aligned} \delta_t &= R_{t+1} + \gamma \cdot Q(S_{t+1}, \underset{a \in \mathcal A}{\text{ arg max}}Q(S_{t+1},a;w);w) - Q(S_t,A_t;w) \\ &= R_{t+1} + \gamma \cdot \underset{a \in \mathcal A}{\text{max}} Q(S_{t+1},a;w) - Q(S_t,A_t;w)) \end{aligned} \]

4.1 Implementation of Temporal_Difference (Q-Learning) Control

PolicyFromQType = Callable[
    [QValueFunctionApprox[S, A], MarkovDecisionProcess[S, A]],
    Policy[S, A]
]
def q_learning(
    mdp: MarkovDecisionProcess[S, A],
    policy_from_q: PolicyFromQType,
    states: NTStateDistribution[S],
    approx_0: QValueFunctionApprox[S, A],
    γ: float,
    max_episode_length: int
) -> Iterator[QValueFunctionApprox[S, A]]:
    q: QValueFunctionApprox[S, A] = approx_0
    yield q
    while True:
        state: NonTerminal[S] = states.sample()
        steps: int = 0
        while isinstance(state, NonTerminal) and steps < max_episode_length:
            policy: Policy[S, A] = policy_from_q(q, mdp)
            action: A = policy.act(state).sample()
            #. next_state, reward = mdp.step(state, action).sample()
            next_state, reward = mdp.transition_action(state, action).sample() #.
            next_return: float = max(
                q((next_state, a))
                for a in mdp.actions(next_state)
            ) if isinstance(next_state, NonTerminal) else 0.
            q = q.update([((state, action), reward + γ * next_return)])
            yield q
            steps += 1
            state = next_state

We run the TAB TD Control (Q-Learning) algorithm on the Inventory problem.

Let us set the capacity \(C=5\), but keep the other parameters as before.

# capacity: int = 2
capacity: int = 5
poisson_lambda: float = 1.0
holding_cost: float = 1.0
stockout_cost: float = 10.0
gamma: float = 0.9
si_mdp: SimpleInventoryMDPCap = SimpleInventoryMDPCap(
    capacity=capacity,
    poisson_lambda=poisson_lambda,
    holding_cost=holding_cost,
    stockout_cost=stockout_cost
)
max_episode_length: int = 100
# epsilon_as_func_of_episodes: Callable[[int], float] = lambda k: k**-0.5
initial_learning_rate: float = 0.1
half_life: float = 10000.0
exponent: float = 1.0
# gamma: float = 0.9
q_learning_epsilon: float = 0.2
initial_qvf_dict: Mapping[Tuple[NonTerminal[InventoryState], int], float] = {
    (s, a): 0. for s in si_mdp.non_terminal_states for a in si_mdp.actions(s)
}
# initial_qvf_dict
learning_rate_func: Callable[[int], float] = learning_rate_schedule(
    initial_learning_rate=initial_learning_rate,
    half_life=half_life,
    exponent=exponent
)
qvfas: Iterator[QValueFunctionApprox[InventoryState, int]] = q_learning(
        mdp=si_mdp,
        policy_from_q=lambda f, m: mc.epsilon_greedy_policy(
            q=f,
            mdp=m,
            ϵ=q_learning_epsilon
        ),
        states=Choose(si_mdp.non_terminal_states),
        approx_0=Tabular(
            values_map=initial_qvf_dict,
            count_to_weight_func=learning_rate_func
        ),
        γ=gamma,
        max_episode_length=max_episode_length
)
qvfas
<generator object q_learning at 0x7fccc04f44d0>

Now we get the final estimate of the Optimal Action-Value Function after n_episodes*max_episode_length. Then we extract from it the estimate of the Optimal State-Value Function and the Optimal Policy.

n_episodes = 10_000
n_updates = n_episodes*max_episode_length
%%time
qvfa_lst = [qvfa for qvfa in itertools.islice(qvfas, n_updates)]
CPU times: user 2min 52s, sys: 13.3 s, total: 3min 6s
Wall time: 2min 55s
final_qvfa: QValueFunctionApprox[InventoryState, int] = iterate.last(qvfa_lst)
final_qvfa
Tabular(values_map={(NonTerminal(state=InventoryState(on_hand=0, on_order=0)), 0): -34.29167989362301, (NonTerminal(state=InventoryState(on_hand=0, on_order=0)), 1): -28.019374282761202, (NonTerminal(state=InventoryState(on_hand=0, on_order=0)), 2): -26.963364564912712, (NonTerminal(state=InventoryState(on_hand=0, on_order=0)), 3): -28.069960994856284, (NonTerminal(state=InventoryState(on_hand=0, on_order=0)), 4): -28.869247283981043, (NonTerminal(state=InventoryState(on_hand=0, on_order=0)), 5): -30.556181243287856, (NonTerminal(state=InventoryState(on_hand=0, on_order=1)), 0): -25.153238171832434, (NonTerminal(state=InventoryState(on_hand=0, on_order=1)), 1): -20.281394896688038, (NonTerminal(state=InventoryState(on_hand=0, on_order=1)), 2): -19.950928140606013, (NonTerminal(state=InventoryState(on_hand=0, on_order=1)), 3): -20.784684662015437, (NonTerminal(state=InventoryState(on_hand=0, on_order=1)), 4): -22.093641772523796, (NonTerminal(state=InventoryState(on_hand=0, on_order=2)), 0): -20.19478258133303, (NonTerminal(state=InventoryState(on_hand=0, on_order=2)), 1): -18.893096534914584, (NonTerminal(state=InventoryState(on_hand=0, on_order=2)), 2): -19.379273590793662, (NonTerminal(state=InventoryState(on_hand=0, on_order=2)), 3): -20.355836068055073, (NonTerminal(state=InventoryState(on_hand=0, on_order=3)), 0): -20.86308913425141, (NonTerminal(state=InventoryState(on_hand=0, on_order=3)), 1): -19.766811430911748, (NonTerminal(state=InventoryState(on_hand=0, on_order=3)), 2): -21.28697236483091, (NonTerminal(state=InventoryState(on_hand=0, on_order=4)), 0): -20.74205917979043, (NonTerminal(state=InventoryState(on_hand=0, on_order=4)), 1): -22.335364962724913, (NonTerminal(state=InventoryState(on_hand=0, on_order=5)), 0): -23.397969626596268, (NonTerminal(state=InventoryState(on_hand=1, on_order=0)), 0): -25.63470756325478, (NonTerminal(state=InventoryState(on_hand=1, on_order=0)), 1): -21.36807528901896, (NonTerminal(state=InventoryState(on_hand=1, on_order=0)), 2): -21.099163467139114, (NonTerminal(state=InventoryState(on_hand=1, on_order=0)), 3): -21.51047077574053, (NonTerminal(state=InventoryState(on_hand=1, on_order=0)), 4): -23.018972972728424, (NonTerminal(state=InventoryState(on_hand=1, on_order=1)), 0): -21.55679273279888, (NonTerminal(state=InventoryState(on_hand=1, on_order=1)), 1): -19.82044156219879, (NonTerminal(state=InventoryState(on_hand=1, on_order=1)), 2): -20.368245151936414, (NonTerminal(state=InventoryState(on_hand=1, on_order=1)), 3): -21.38944048490033, (NonTerminal(state=InventoryState(on_hand=1, on_order=2)), 0): -21.050307002149907, (NonTerminal(state=InventoryState(on_hand=1, on_order=2)), 1): -20.84792154775406, (NonTerminal(state=InventoryState(on_hand=1, on_order=2)), 2): -22.621742143231202, (NonTerminal(state=InventoryState(on_hand=1, on_order=3)), 0): -21.83612334536198, (NonTerminal(state=InventoryState(on_hand=1, on_order=3)), 1): -22.901545610933507, (NonTerminal(state=InventoryState(on_hand=1, on_order=4)), 0): -24.259325423298947, (NonTerminal(state=InventoryState(on_hand=2, on_order=0)), 0): -22.98938552312266, (NonTerminal(state=InventoryState(on_hand=2, on_order=0)), 1): -20.84338106185867, (NonTerminal(state=InventoryState(on_hand=2, on_order=0)), 2): -21.22848372377584, (NonTerminal(state=InventoryState(on_hand=2, on_order=0)), 3): -22.62627192946876, (NonTerminal(state=InventoryState(on_hand=2, on_order=1)), 0): -22.12797150580425, (NonTerminal(state=InventoryState(on_hand=2, on_order=1)), 1): -21.995874198463067, (NonTerminal(state=InventoryState(on_hand=2, on_order=1)), 2): -22.86076952824054, (NonTerminal(state=InventoryState(on_hand=2, on_order=2)), 0): -22.875950561803087, (NonTerminal(state=InventoryState(on_hand=2, on_order=2)), 1): -23.951456599301213, (NonTerminal(state=InventoryState(on_hand=2, on_order=3)), 0): -24.787545606776312, (NonTerminal(state=InventoryState(on_hand=3, on_order=0)), 0): -23.25372253651443, (NonTerminal(state=InventoryState(on_hand=3, on_order=0)), 1): -22.929466105679385, (NonTerminal(state=InventoryState(on_hand=3, on_order=0)), 2): -24.009915686734374, (NonTerminal(state=InventoryState(on_hand=3, on_order=1)), 0): -24.078312289662236, (NonTerminal(state=InventoryState(on_hand=3, on_order=1)), 1): -24.9649236826972, (NonTerminal(state=InventoryState(on_hand=3, on_order=2)), 0): -26.058681205609766, (NonTerminal(state=InventoryState(on_hand=4, on_order=0)), 0): -25.071399529390735, (NonTerminal(state=InventoryState(on_hand=4, on_order=0)), 1): -26.20134809299714, (NonTerminal(state=InventoryState(on_hand=4, on_order=1)), 0): -26.853538764992972, (NonTerminal(state=InventoryState(on_hand=5, on_order=0)), 0): -27.74356947452911}, counts_map={(NonTerminal(state=InventoryState(on_hand=2, on_order=2)), 0): 13484, (NonTerminal(state=InventoryState(on_hand=4, on_order=0)), 0): 68826, (NonTerminal(state=InventoryState(on_hand=3, on_order=0)), 0): 28352, (NonTerminal(state=InventoryState(on_hand=0, on_order=0)), 0): 647, (NonTerminal(state=InventoryState(on_hand=0, on_order=0)), 1): 710, (NonTerminal(state=InventoryState(on_hand=0, on_order=1)), 4): 3568, (NonTerminal(state=InventoryState(on_hand=1, on_order=4)), 0): 2312, (NonTerminal(state=InventoryState(on_hand=3, on_order=0)), 1): 69916, (NonTerminal(state=InventoryState(on_hand=2, on_order=1)), 2): 11761, (NonTerminal(state=InventoryState(on_hand=2, on_order=2)), 1): 1734, (NonTerminal(state=InventoryState(on_hand=4, on_order=1)), 0): 7998, (NonTerminal(state=InventoryState(on_hand=3, on_order=0)), 2): 7351, (NonTerminal(state=InventoryState(on_hand=3, on_order=2)), 0): 8904, (NonTerminal(state=InventoryState(on_hand=1, on_order=1)), 0): 6761, (NonTerminal(state=InventoryState(on_hand=2, on_order=0)), 0): 3933, (NonTerminal(state=InventoryState(on_hand=2, on_order=0)), 1): 62531, (NonTerminal(state=InventoryState(on_hand=2, on_order=1)), 0): 52241, (NonTerminal(state=InventoryState(on_hand=2, on_order=0)), 2): 4399, (NonTerminal(state=InventoryState(on_hand=3, on_order=1)), 0): 76320, (NonTerminal(state=InventoryState(on_hand=4, on_order=0)), 1): 8234, (NonTerminal(state=InventoryState(on_hand=3, on_order=1)), 1): 9045, (NonTerminal(state=InventoryState(on_hand=2, on_order=1)), 1): 107533, (NonTerminal(state=InventoryState(on_hand=1, on_order=1)), 2): 7817, (NonTerminal(state=InventoryState(on_hand=1, on_order=2)), 0): 13653, (NonTerminal(state=InventoryState(on_hand=5, on_order=0)), 0): 15678, (NonTerminal(state=InventoryState(on_hand=2, on_order=0)), 3): 3882, (NonTerminal(state=InventoryState(on_hand=2, on_order=3)), 0): 6015, (NonTerminal(state=InventoryState(on_hand=0, on_order=1)), 0): 3486, (NonTerminal(state=InventoryState(on_hand=1, on_order=0)), 0): 1423, (NonTerminal(state=InventoryState(on_hand=0, on_order=0)), 2): 15780, (NonTerminal(state=InventoryState(on_hand=0, on_order=2)), 0): 4337, (NonTerminal(state=InventoryState(on_hand=1, on_order=3)), 1): 910, (NonTerminal(state=InventoryState(on_hand=1, on_order=0)), 1): 2511, (NonTerminal(state=InventoryState(on_hand=1, on_order=1)), 1): 111605, (NonTerminal(state=InventoryState(on_hand=1, on_order=1)), 3): 6713, (NonTerminal(state=InventoryState(on_hand=1, on_order=3)), 0): 6805, (NonTerminal(state=InventoryState(on_hand=1, on_order=0)), 2): 28968, (NonTerminal(state=InventoryState(on_hand=0, on_order=2)), 1): 71569, (NonTerminal(state=InventoryState(on_hand=0, on_order=0)), 3): 764, (NonTerminal(state=InventoryState(on_hand=0, on_order=3)), 0): 2557, (NonTerminal(state=InventoryState(on_hand=0, on_order=1)), 1): 5372, (NonTerminal(state=InventoryState(on_hand=0, on_order=1)), 2): 71357, (NonTerminal(state=InventoryState(on_hand=0, on_order=0)), 4): 697, (NonTerminal(state=InventoryState(on_hand=0, on_order=4)), 0): 3802, (NonTerminal(state=InventoryState(on_hand=1, on_order=0)), 3): 1516, (NonTerminal(state=InventoryState(on_hand=0, on_order=3)), 1): 5035, (NonTerminal(state=InventoryState(on_hand=0, on_order=0)), 5): 674, (NonTerminal(state=InventoryState(on_hand=0, on_order=5)), 0): 1114, (NonTerminal(state=InventoryState(on_hand=1, on_order=0)), 4): 1541, (NonTerminal(state=InventoryState(on_hand=1, on_order=2)), 1): 30459, (NonTerminal(state=InventoryState(on_hand=0, on_order=2)), 2): 5026, (NonTerminal(state=InventoryState(on_hand=0, on_order=1)), 3): 3551, (NonTerminal(state=InventoryState(on_hand=0, on_order=3)), 2): 665, (NonTerminal(state=InventoryState(on_hand=0, on_order=4)), 1): 585, (NonTerminal(state=InventoryState(on_hand=0, on_order=2)), 3): 4299, (NonTerminal(state=InventoryState(on_hand=1, on_order=2)), 2): 3273}, count_to_weight_func=<function learning_rate_schedule.<locals>.lr_func at 0x7fcccc7f45f0>)
def get_vf_and_policy_from_qvf(
    mdp: FiniteMarkovDecisionProcess[S, A],
    qvf: QValueFunctionApprox[S, A]
) -> Tuple[V[S], FiniteDeterministicPolicy[S, A]]:
    opt_vf: V[S] = {
        s: max(qvf((s, a)) for a in mdp.actions(s))
        for s in mdp.non_terminal_states
    }
    opt_policy: FiniteDeterministicPolicy[S, A] = \
        FiniteDeterministicPolicy({
            s.state: qvf.argmax((s, a) for a in mdp.actions(s))[1]
            for s in mdp.non_terminal_states
        })
    return opt_vf, opt_policy
opt_svf, opt_pol = get_vf_and_policy_from_qvf(
    mdp=si_mdp,
    qvf=final_qvfa
)
print(f"TD (Q-Learning) Optimal Value Function with {n_updates:d} updates")
pprint(opt_svf)
TD (Q-Learning) Optimal Value Function with 1000000 updates
{NonTerminal(state=InventoryState(on_hand=0, on_order=0)): -26.963364564912712,
 NonTerminal(state=InventoryState(on_hand=0, on_order=1)): -19.950928140606013,
 NonTerminal(state=InventoryState(on_hand=0, on_order=2)): -18.893096534914584,
 NonTerminal(state=InventoryState(on_hand=0, on_order=3)): -19.766811430911748,
 NonTerminal(state=InventoryState(on_hand=0, on_order=4)): -20.74205917979043,
 NonTerminal(state=InventoryState(on_hand=0, on_order=5)): -23.397969626596268,
 NonTerminal(state=InventoryState(on_hand=1, on_order=0)): -21.099163467139114,
 NonTerminal(state=InventoryState(on_hand=1, on_order=1)): -19.82044156219879,
 NonTerminal(state=InventoryState(on_hand=1, on_order=2)): -20.84792154775406,
 NonTerminal(state=InventoryState(on_hand=1, on_order=3)): -21.83612334536198,
 NonTerminal(state=InventoryState(on_hand=1, on_order=4)): -24.259325423298947,
 NonTerminal(state=InventoryState(on_hand=2, on_order=0)): -20.84338106185867,
 NonTerminal(state=InventoryState(on_hand=2, on_order=1)): -21.995874198463067,
 NonTerminal(state=InventoryState(on_hand=2, on_order=2)): -22.875950561803087,
 NonTerminal(state=InventoryState(on_hand=2, on_order=3)): -24.787545606776312,
 NonTerminal(state=InventoryState(on_hand=3, on_order=0)): -22.929466105679385,
 NonTerminal(state=InventoryState(on_hand=3, on_order=1)): -24.078312289662236,
 NonTerminal(state=InventoryState(on_hand=3, on_order=2)): -26.058681205609766,
 NonTerminal(state=InventoryState(on_hand=4, on_order=0)): -25.071399529390735,
 NonTerminal(state=InventoryState(on_hand=4, on_order=1)): -26.853538764992972,
 NonTerminal(state=InventoryState(on_hand=5, on_order=0)): -27.74356947452911}
print(f"TD (Q-Learning) Optimal Policy with {n_updates:d} updates")
pprint(opt_pol)
TD (Q-Learning) Optimal Policy with 1000000 updates
For State InventoryState(on_hand=0, on_order=0): Do Action 2
For State InventoryState(on_hand=0, on_order=1): Do Action 2
For State InventoryState(on_hand=0, on_order=2): Do Action 1
For State InventoryState(on_hand=0, on_order=3): Do Action 1
For State InventoryState(on_hand=0, on_order=4): Do Action 0
For State InventoryState(on_hand=0, on_order=5): Do Action 0
For State InventoryState(on_hand=1, on_order=0): Do Action 2
For State InventoryState(on_hand=1, on_order=1): Do Action 1
For State InventoryState(on_hand=1, on_order=2): Do Action 1
For State InventoryState(on_hand=1, on_order=3): Do Action 0
For State InventoryState(on_hand=1, on_order=4): Do Action 0
For State InventoryState(on_hand=2, on_order=0): Do Action 1
For State InventoryState(on_hand=2, on_order=1): Do Action 1
For State InventoryState(on_hand=2, on_order=2): Do Action 0
For State InventoryState(on_hand=2, on_order=3): Do Action 0
For State InventoryState(on_hand=3, on_order=0): Do Action 1
For State InventoryState(on_hand=3, on_order=1): Do Action 0
For State InventoryState(on_hand=3, on_order=2): Do Action 0
For State InventoryState(on_hand=4, on_order=0): Do Action 0
For State InventoryState(on_hand=4, on_order=1): Do Action 0
For State InventoryState(on_hand=5, on_order=0): Do Action 0

For comparison, we run a Value Iteration to find the true Optimal Value Function and Optimal Policy.

true_opt_svf, true_opt_pol = value_iteration_result(mdp=si_mdp, gamma=gamma)
print("True Optimal State Value Function")
pprint(true_opt_svf)
True Optimal State Value Function
{NonTerminal(state=InventoryState(on_hand=0, on_order=0)): -26.98163492786722,
 NonTerminal(state=InventoryState(on_hand=0, on_order=1)): -19.9909558006178,
 NonTerminal(state=InventoryState(on_hand=0, on_order=2)): -18.86849301795165,
 NonTerminal(state=InventoryState(on_hand=0, on_order=3)): -19.934022635857023,
 NonTerminal(state=InventoryState(on_hand=0, on_order=4)): -20.91848526863397,
 NonTerminal(state=InventoryState(on_hand=0, on_order=5)): -22.77205311116058,
 NonTerminal(state=InventoryState(on_hand=1, on_order=0)): -20.9909558006178,
 NonTerminal(state=InventoryState(on_hand=1, on_order=1)): -19.86849301795165,
 NonTerminal(state=InventoryState(on_hand=1, on_order=2)): -20.934022635857026,
 NonTerminal(state=InventoryState(on_hand=1, on_order=3)): -21.918485268633972,
 NonTerminal(state=InventoryState(on_hand=1, on_order=4)): -23.77205311116058,
 NonTerminal(state=InventoryState(on_hand=2, on_order=0)): -20.86849301795165,
 NonTerminal(state=InventoryState(on_hand=2, on_order=1)): -21.934022635857023,
 NonTerminal(state=InventoryState(on_hand=2, on_order=2)): -22.91848526863397,
 NonTerminal(state=InventoryState(on_hand=2, on_order=3)): -24.77205311116058,
 NonTerminal(state=InventoryState(on_hand=3, on_order=0)): -22.934022635857026,
 NonTerminal(state=InventoryState(on_hand=3, on_order=1)): -23.918485268633972,
 NonTerminal(state=InventoryState(on_hand=3, on_order=2)): -25.772053111160584,
 NonTerminal(state=InventoryState(on_hand=4, on_order=0)): -24.91848526863397,
 NonTerminal(state=InventoryState(on_hand=4, on_order=1)): -26.772053111160577,
 NonTerminal(state=InventoryState(on_hand=5, on_order=0)): -27.772053111160577}
print("True Optimal Policy")
pprint(true_opt_pol)
True Optimal Policy
For State InventoryState(on_hand=0, on_order=0): Do Action 2
For State InventoryState(on_hand=0, on_order=1): Do Action 2
For State InventoryState(on_hand=0, on_order=2): Do Action 1
For State InventoryState(on_hand=0, on_order=3): Do Action 1
For State InventoryState(on_hand=0, on_order=4): Do Action 0
For State InventoryState(on_hand=0, on_order=5): Do Action 0
For State InventoryState(on_hand=1, on_order=0): Do Action 2
For State InventoryState(on_hand=1, on_order=1): Do Action 1
For State InventoryState(on_hand=1, on_order=2): Do Action 1
For State InventoryState(on_hand=1, on_order=3): Do Action 0
For State InventoryState(on_hand=1, on_order=4): Do Action 0
For State InventoryState(on_hand=2, on_order=0): Do Action 1
For State InventoryState(on_hand=2, on_order=1): Do Action 1
For State InventoryState(on_hand=2, on_order=2): Do Action 0
For State InventoryState(on_hand=2, on_order=3): Do Action 0
For State InventoryState(on_hand=3, on_order=0): Do Action 1
For State InventoryState(on_hand=3, on_order=1): Do Action 0
For State InventoryState(on_hand=3, on_order=2): Do Action 0
For State InventoryState(on_hand=4, on_order=0): Do Action 0
For State InventoryState(on_hand=4, on_order=1): Do Action 0
For State InventoryState(on_hand=5, on_order=0): Do Action 0

Now we compare values by state for the State Value Function

[(true_opt_svf[s], opt_svf[s]) for s in si_mdp.non_terminal_states]
[(-26.98163492786722, -26.963364564912712),
 (-19.9909558006178, -19.950928140606013),
 (-18.86849301795165, -18.893096534914584),
 (-19.934022635857023, -19.766811430911748),
 (-20.91848526863397, -20.74205917979043),
 (-22.77205311116058, -23.397969626596268),
 (-20.9909558006178, -21.099163467139114),
 (-19.86849301795165, -19.82044156219879),
 (-20.934022635857026, -20.84792154775406),
 (-21.918485268633972, -21.83612334536198),
 (-23.77205311116058, -24.259325423298947),
 (-20.86849301795165, -20.84338106185867),
 (-21.934022635857023, -21.995874198463067),
 (-22.91848526863397, -22.875950561803087),
 (-24.77205311116058, -24.787545606776312),
 (-22.934022635857026, -22.929466105679385),
 (-23.918485268633972, -24.078312289662236),
 (-25.772053111160584, -26.058681205609766),
 (-24.91848526863397, -25.071399529390735),
 (-26.772053111160577, -26.853538764992972),
 (-27.772053111160577, -27.74356947452911)]

We also compare values by state for the Policy

[(true_opt_pol.policy_map[s.state], opt_pol.policy_map[s.state]) for s in si_mdp.non_terminal_states]
[(Constant(value=2), Constant(value=2)),
 (Constant(value=2), Constant(value=2)),
 (Constant(value=1), Constant(value=1)),
 (Constant(value=1), Constant(value=1)),
 (Constant(value=0), Constant(value=0)),
 (Constant(value=0), Constant(value=0)),
 (Constant(value=2), Constant(value=2)),
 (Constant(value=1), Constant(value=1)),
 (Constant(value=1), Constant(value=1)),
 (Constant(value=0), Constant(value=0)),
 (Constant(value=0), Constant(value=0)),
 (Constant(value=1), Constant(value=1)),
 (Constant(value=1), Constant(value=1)),
 (Constant(value=0), Constant(value=0)),
 (Constant(value=0), Constant(value=0)),
 (Constant(value=1), Constant(value=1)),
 (Constant(value=0), Constant(value=0)),
 (Constant(value=0), Constant(value=0)),
 (Constant(value=0), Constant(value=0)),
 (Constant(value=0), Constant(value=0)),
 (Constant(value=0), Constant(value=0))]

4.2 Visualize

Let us visualize the convergence of the Action Value Function (Q) for each of the states:

qvfa_lst[10]
Tabular(values_map={(NonTerminal(state=InventoryState(on_hand=0, on_order=0)), 0): -1.0, (NonTerminal(state=InventoryState(on_hand=0, on_order=0)), 1): -1.0, (NonTerminal(state=InventoryState(on_hand=0, on_order=0)), 2): 0.0, (NonTerminal(state=InventoryState(on_hand=0, on_order=0)), 3): 0.0, (NonTerminal(state=InventoryState(on_hand=0, on_order=0)), 4): 0.0, (NonTerminal(state=InventoryState(on_hand=0, on_order=0)), 5): 0.0, (NonTerminal(state=InventoryState(on_hand=0, on_order=1)), 0): 0.0, (NonTerminal(state=InventoryState(on_hand=0, on_order=1)), 1): 0.0, (NonTerminal(state=InventoryState(on_hand=0, on_order=1)), 2): 0.0, (NonTerminal(state=InventoryState(on_hand=0, on_order=1)), 3): 0.0, (NonTerminal(state=InventoryState(on_hand=0, on_order=1)), 4): 0.0, (NonTerminal(state=InventoryState(on_hand=0, on_order=2)), 0): 0.0, (NonTerminal(state=InventoryState(on_hand=0, on_order=2)), 1): 0.0, (NonTerminal(state=InventoryState(on_hand=0, on_order=2)), 2): 0.0, (NonTerminal(state=InventoryState(on_hand=0, on_order=2)), 3): 0.0, (NonTerminal(state=InventoryState(on_hand=0, on_order=3)), 0): 0.0, (NonTerminal(state=InventoryState(on_hand=0, on_order=3)), 1): 0.0, (NonTerminal(state=InventoryState(on_hand=0, on_order=3)), 2): 0.0, (NonTerminal(state=InventoryState(on_hand=0, on_order=4)), 0): 0.0, (NonTerminal(state=InventoryState(on_hand=0, on_order=4)), 1): 0.0, (NonTerminal(state=InventoryState(on_hand=0, on_order=5)), 0): 0.0, (NonTerminal(state=InventoryState(on_hand=1, on_order=0)), 0): 0.0, (NonTerminal(state=InventoryState(on_hand=1, on_order=0)), 1): 0.0, (NonTerminal(state=InventoryState(on_hand=1, on_order=0)), 2): 0.0, (NonTerminal(state=InventoryState(on_hand=1, on_order=0)), 3): 0.0, (NonTerminal(state=InventoryState(on_hand=1, on_order=0)), 4): 0.0, (NonTerminal(state=InventoryState(on_hand=1, on_order=1)), 0): 0.0, (NonTerminal(state=InventoryState(on_hand=1, on_order=1)), 1): 0.0, (NonTerminal(state=InventoryState(on_hand=1, on_order=1)), 2): 0.0, (NonTerminal(state=InventoryState(on_hand=1, on_order=1)), 3): 0.0, (NonTerminal(state=InventoryState(on_hand=1, on_order=2)), 0): 0.0, (NonTerminal(state=InventoryState(on_hand=1, on_order=2)), 1): 0.0, (NonTerminal(state=InventoryState(on_hand=1, on_order=2)), 2): 0.0, (NonTerminal(state=InventoryState(on_hand=1, on_order=3)), 0): 0.0, (NonTerminal(state=InventoryState(on_hand=1, on_order=3)), 1): 0.0, (NonTerminal(state=InventoryState(on_hand=1, on_order=4)), 0): -0.1, (NonTerminal(state=InventoryState(on_hand=2, on_order=0)), 0): 0.0, (NonTerminal(state=InventoryState(on_hand=2, on_order=0)), 1): 0.0, (NonTerminal(state=InventoryState(on_hand=2, on_order=0)), 2): 0.0, (NonTerminal(state=InventoryState(on_hand=2, on_order=0)), 3): 0.0, (NonTerminal(state=InventoryState(on_hand=2, on_order=1)), 0): 0.0, (NonTerminal(state=InventoryState(on_hand=2, on_order=1)), 1): 0.0, (NonTerminal(state=InventoryState(on_hand=2, on_order=1)), 2): -0.2, (NonTerminal(state=InventoryState(on_hand=2, on_order=2)), 0): -0.2, (NonTerminal(state=InventoryState(on_hand=2, on_order=2)), 1): -0.2, (NonTerminal(state=InventoryState(on_hand=2, on_order=3)), 0): 0.0, (NonTerminal(state=InventoryState(on_hand=3, on_order=0)), 0): -0.3233369264429329, (NonTerminal(state=InventoryState(on_hand=3, on_order=0)), 1): -0.30000000000000004, (NonTerminal(state=InventoryState(on_hand=3, on_order=0)), 2): 0.0, (NonTerminal(state=InventoryState(on_hand=3, on_order=1)), 0): 0.0, (NonTerminal(state=InventoryState(on_hand=3, on_order=1)), 1): 0.0, (NonTerminal(state=InventoryState(on_hand=3, on_order=2)), 0): 0.0, (NonTerminal(state=InventoryState(on_hand=4, on_order=0)), 0): -0.4, (NonTerminal(state=InventoryState(on_hand=4, on_order=0)), 1): 0.0, (NonTerminal(state=InventoryState(on_hand=4, on_order=1)), 0): 0.0, (NonTerminal(state=InventoryState(on_hand=5, on_order=0)), 0): 0.0}, counts_map={(NonTerminal(state=InventoryState(on_hand=2, on_order=2)), 0): 1, (NonTerminal(state=InventoryState(on_hand=4, on_order=0)), 0): 1, (NonTerminal(state=InventoryState(on_hand=3, on_order=0)), 0): 1, (NonTerminal(state=InventoryState(on_hand=0, on_order=0)), 0): 1, (NonTerminal(state=InventoryState(on_hand=0, on_order=0)), 1): 1, (NonTerminal(state=InventoryState(on_hand=0, on_order=1)), 4): 1, (NonTerminal(state=InventoryState(on_hand=1, on_order=4)), 0): 1, (NonTerminal(state=InventoryState(on_hand=3, on_order=0)), 1): 1, (NonTerminal(state=InventoryState(on_hand=2, on_order=1)), 2): 1, (NonTerminal(state=InventoryState(on_hand=2, on_order=2)), 1): 1}, count_to_weight_func=<function learning_rate_schedule.<locals>.lr_func at 0x7fcccc7f45f0>)
qvfa_lst[10].values_map
{(NonTerminal(state=InventoryState(on_hand=0, on_order=0)), 0): -1.0,
 (NonTerminal(state=InventoryState(on_hand=0, on_order=0)), 1): -1.0,
 (NonTerminal(state=InventoryState(on_hand=0, on_order=0)), 2): 0.0,
 (NonTerminal(state=InventoryState(on_hand=0, on_order=0)), 3): 0.0,
 (NonTerminal(state=InventoryState(on_hand=0, on_order=0)), 4): 0.0,
 (NonTerminal(state=InventoryState(on_hand=0, on_order=0)), 5): 0.0,
 (NonTerminal(state=InventoryState(on_hand=0, on_order=1)), 0): 0.0,
 (NonTerminal(state=InventoryState(on_hand=0, on_order=1)), 1): 0.0,
 (NonTerminal(state=InventoryState(on_hand=0, on_order=1)), 2): 0.0,
 (NonTerminal(state=InventoryState(on_hand=0, on_order=1)), 3): 0.0,
 (NonTerminal(state=InventoryState(on_hand=0, on_order=1)), 4): 0.0,
 (NonTerminal(state=InventoryState(on_hand=0, on_order=2)), 0): 0.0,
 (NonTerminal(state=InventoryState(on_hand=0, on_order=2)), 1): 0.0,
 (NonTerminal(state=InventoryState(on_hand=0, on_order=2)), 2): 0.0,
 (NonTerminal(state=InventoryState(on_hand=0, on_order=2)), 3): 0.0,
 (NonTerminal(state=InventoryState(on_hand=0, on_order=3)), 0): 0.0,
 (NonTerminal(state=InventoryState(on_hand=0, on_order=3)), 1): 0.0,
 (NonTerminal(state=InventoryState(on_hand=0, on_order=3)), 2): 0.0,
 (NonTerminal(state=InventoryState(on_hand=0, on_order=4)), 0): 0.0,
 (NonTerminal(state=InventoryState(on_hand=0, on_order=4)), 1): 0.0,
 (NonTerminal(state=InventoryState(on_hand=0, on_order=5)), 0): 0.0,
 (NonTerminal(state=InventoryState(on_hand=1, on_order=0)), 0): 0.0,
 (NonTerminal(state=InventoryState(on_hand=1, on_order=0)), 1): 0.0,
 (NonTerminal(state=InventoryState(on_hand=1, on_order=0)), 2): 0.0,
 (NonTerminal(state=InventoryState(on_hand=1, on_order=0)), 3): 0.0,
 (NonTerminal(state=InventoryState(on_hand=1, on_order=0)), 4): 0.0,
 (NonTerminal(state=InventoryState(on_hand=1, on_order=1)), 0): 0.0,
 (NonTerminal(state=InventoryState(on_hand=1, on_order=1)), 1): 0.0,
 (NonTerminal(state=InventoryState(on_hand=1, on_order=1)), 2): 0.0,
 (NonTerminal(state=InventoryState(on_hand=1, on_order=1)), 3): 0.0,
 (NonTerminal(state=InventoryState(on_hand=1, on_order=2)), 0): 0.0,
 (NonTerminal(state=InventoryState(on_hand=1, on_order=2)), 1): 0.0,
 (NonTerminal(state=InventoryState(on_hand=1, on_order=2)), 2): 0.0,
 (NonTerminal(state=InventoryState(on_hand=1, on_order=3)), 0): 0.0,
 (NonTerminal(state=InventoryState(on_hand=1, on_order=3)), 1): 0.0,
 (NonTerminal(state=InventoryState(on_hand=1, on_order=4)), 0): -0.1,
 (NonTerminal(state=InventoryState(on_hand=2, on_order=0)), 0): 0.0,
 (NonTerminal(state=InventoryState(on_hand=2, on_order=0)), 1): 0.0,
 (NonTerminal(state=InventoryState(on_hand=2, on_order=0)), 2): 0.0,
 (NonTerminal(state=InventoryState(on_hand=2, on_order=0)), 3): 0.0,
 (NonTerminal(state=InventoryState(on_hand=2, on_order=1)), 0): 0.0,
 (NonTerminal(state=InventoryState(on_hand=2, on_order=1)), 1): 0.0,
 (NonTerminal(state=InventoryState(on_hand=2, on_order=1)), 2): -0.2,
 (NonTerminal(state=InventoryState(on_hand=2, on_order=2)), 0): -0.2,
 (NonTerminal(state=InventoryState(on_hand=2, on_order=2)), 1): -0.2,
 (NonTerminal(state=InventoryState(on_hand=2, on_order=3)), 0): 0.0,
 (NonTerminal(state=InventoryState(on_hand=3, on_order=0)),
  0): -0.3233369264429329,
 (NonTerminal(state=InventoryState(on_hand=3, on_order=0)),
  1): -0.30000000000000004,
 (NonTerminal(state=InventoryState(on_hand=3, on_order=0)), 2): 0.0,
 (NonTerminal(state=InventoryState(on_hand=3, on_order=1)), 0): 0.0,
 (NonTerminal(state=InventoryState(on_hand=3, on_order=1)), 1): 0.0,
 (NonTerminal(state=InventoryState(on_hand=3, on_order=2)), 0): 0.0,
 (NonTerminal(state=InventoryState(on_hand=4, on_order=0)), 0): -0.4,
 (NonTerminal(state=InventoryState(on_hand=4, on_order=0)), 1): 0.0,
 (NonTerminal(state=InventoryState(on_hand=4, on_order=1)), 0): 0.0,
 (NonTerminal(state=InventoryState(on_hand=5, on_order=0)), 0): 0.0}
qvfa_lst[10].counts_map
{(NonTerminal(state=InventoryState(on_hand=2, on_order=2)), 0): 1,
 (NonTerminal(state=InventoryState(on_hand=4, on_order=0)), 0): 1,
 (NonTerminal(state=InventoryState(on_hand=3, on_order=0)), 0): 1,
 (NonTerminal(state=InventoryState(on_hand=0, on_order=0)), 0): 1,
 (NonTerminal(state=InventoryState(on_hand=0, on_order=0)), 1): 1,
 (NonTerminal(state=InventoryState(on_hand=0, on_order=1)), 4): 1,
 (NonTerminal(state=InventoryState(on_hand=1, on_order=4)), 0): 1,
 (NonTerminal(state=InventoryState(on_hand=3, on_order=0)), 1): 1,
 (NonTerminal(state=InventoryState(on_hand=2, on_order=1)), 2): 1,
 (NonTerminal(state=InventoryState(on_hand=2, on_order=2)), 1): 1}

Let us visualize how the Action Value Function for each (state, action) pair converges during the operation of the Monte-Carlo algorithm.

values_dicts = [(vfa.values_map) for vfa in qvfa_lst]
# values_dicts
# https://stackoverflow.com/questions/5946236/how-to-merge-dicts-collecting-values-from-matching-keys
from collections import defaultdict
ds = values_dicts
merged_dict = defaultdict(list)
for d in ds: #input dicts
    for key, value in d.items():
        merged_dict[key].append(value)
# merged_dict
len(merged_dict)
56
import matplotlib.pyplot as plt
fig,axs = plt.subplots(figsize=(13,10))
axs.set_xlabel('Iterations', fontsize=20)
axs.set_title(f'Convergence of action value functions during Q-Learning', fontsize=24)
for it in merged_dict.items():
  axs.plot(it[1], label=f'{it[0][0].state}, {it[0][1]}')
# axs.legend(fontsize=15);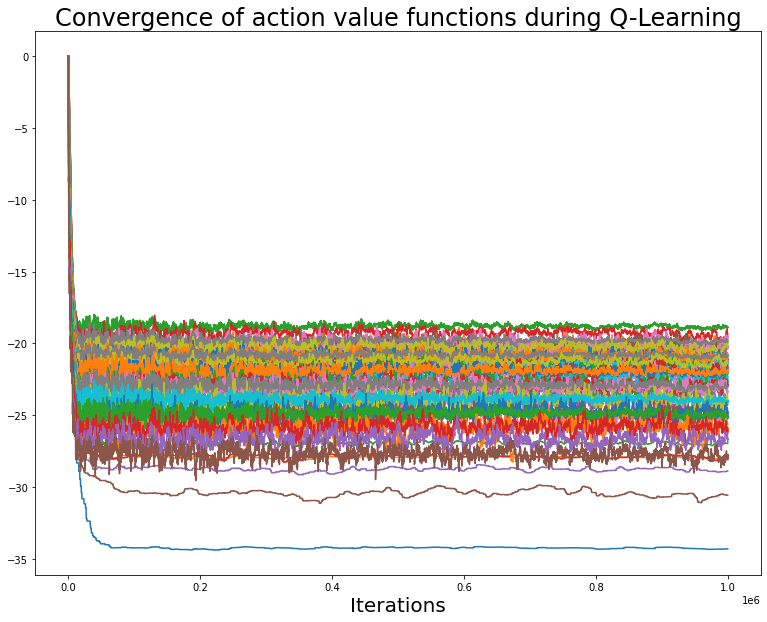

3.5 Performance of optimal policy vs other policies

import numpy as np
print('capacity =', capacity)
print('poisson_lambda =', poisson_lambda) 
print('holding_cost =', holding_cost)
print('stockout_cost =', stockout_cost)
print('gamma =', gamma)
capacity = 5
poisson_lambda = 1.0
holding_cost = 1.0
stockout_cost = 10.0
gamma = 0.9
n_steps = 2_000 #number of simulation steps
class SimpleInventoryDeterministicPolicy(DeterministicPolicy[InventoryState, int]):
  def __init__(self, reorder_point: int):
    self.reorder_point: int = reorder_point
    def action_for(s: InventoryState) -> int:
      return max(self.reorder_point - s.inventory_position(), 0)
    super().__init__(action_for)
# 
# start state distribution
ssd = Choose(si_mdp.non_terminal_states)
# ssd

3.5.1 Deterministic Policy with Reorder Point set to Capacity (Maximum Inventory)

\(\theta = \text{max}(r - (\alpha + \beta), 0)\)

where: - \(\theta \in \mathbb Z_{\ge0}\) is the order quantity - \(r \in \mathbb Z_{\ge0}\) is the reorder point below which reordering is allowed. - \(\alpha\) is the on-hand inventory - \(\beta\) is the on-order inventory - \((\alpha,\beta)\) is the state

We set \(r = C\) where \(C\) is the inventory capacity for the item.

reorder_point_pol_1 = capacity; reorder_point_pol_1
5
pol_1 = SimpleInventoryDeterministicPolicy(reorder_point=reorder_point_pol_1); pol_1
SimpleInventoryDeterministicPolicy(action_for=<function SimpleInventoryDeterministicPolicy.__init__.<locals>.action_for at 0x7fcccc7f4d40>)
step_gen = si_mdp.simulate_action(
    start_state_distribution=ssd, 
    policy=pol_1) 
step_lst = list(itertools.islice(step_gen, n_steps))
pprint(step_lst[:5])
[TransitionStep(state=NonTerminal(state=InventoryState(on_hand=4, on_order=1)), action=0, next_state=NonTerminal(state=InventoryState(on_hand=5, on_order=0)), reward=-4.0),
 TransitionStep(state=NonTerminal(state=InventoryState(on_hand=5, on_order=0)), action=0, next_state=NonTerminal(state=InventoryState(on_hand=0, on_order=0)), reward=-5.006889227394354),
 TransitionStep(state=NonTerminal(state=InventoryState(on_hand=0, on_order=0)), action=5, next_state=NonTerminal(state=InventoryState(on_hand=0, on_order=5)), reward=-10.0),
 TransitionStep(state=NonTerminal(state=InventoryState(on_hand=0, on_order=5)), action=0, next_state=NonTerminal(state=InventoryState(on_hand=5, on_order=0)), reward=-0.0),
 TransitionStep(state=NonTerminal(state=InventoryState(on_hand=5, on_order=0)), action=0, next_state=NonTerminal(state=InventoryState(on_hand=5, on_order=0)), reward=-5.0)]
list_of_tuples = [((step.state.state.on_hand,step.state.state.on_order), step.action, (step.next_state.state.on_hand,step.next_state.state.on_order), step.reward) for step in step_lst]
# list_of_tuples
states, actions, next_states, rewards = [list(tup) for tup in zip(*list_of_tuples)]
cum_reward_pol_1 = np.cumsum(rewards)

3.5.2 Deterministic Policy with Reorder Point set to 1 (Minimum Inventory)

\(\theta = \text{max}(r - (\alpha + \beta), 0)\)

where: - \(\theta \in \mathbb Z_{\ge0}\) is the order quantity - \(r \in \mathbb Z_{\ge0}\) is the reorder point below which reordering is allowed. - \(\alpha\) is the on-hand inventory - \(\beta\) is the on-order inventory - \((\alpha,\beta)\) is the state

We set \(r = 1\).

reorder_point_pol_2 = 1; reorder_point_pol_2
1
pol_2 = SimpleInventoryDeterministicPolicy(reorder_point=reorder_point_pol_2); pol_2
SimpleInventoryDeterministicPolicy(action_for=<function SimpleInventoryDeterministicPolicy.__init__.<locals>.action_for at 0x7fcccc7e9b90>)
step_gen = si_mdp.simulate_action(
    start_state_distribution=ssd, 
    policy=pol_2) 
step_lst = list(itertools.islice(step_gen, n_steps))
pprint(step_lst[:5])
[TransitionStep(state=NonTerminal(state=InventoryState(on_hand=0, on_order=0)), action=1, next_state=NonTerminal(state=InventoryState(on_hand=0, on_order=1)), reward=-10.0),
 TransitionStep(state=NonTerminal(state=InventoryState(on_hand=0, on_order=1)), action=0, next_state=NonTerminal(state=InventoryState(on_hand=0, on_order=0)), reward=-3.6787944117144233),
 TransitionStep(state=NonTerminal(state=InventoryState(on_hand=0, on_order=0)), action=1, next_state=NonTerminal(state=InventoryState(on_hand=0, on_order=1)), reward=-10.0),
 TransitionStep(state=NonTerminal(state=InventoryState(on_hand=0, on_order=1)), action=0, next_state=NonTerminal(state=InventoryState(on_hand=0, on_order=0)), reward=-3.6787944117144233),
 TransitionStep(state=NonTerminal(state=InventoryState(on_hand=0, on_order=0)), action=1, next_state=NonTerminal(state=InventoryState(on_hand=0, on_order=1)), reward=-10.0)]
list_of_tuples = [((step.state.state.on_hand,step.state.state.on_order), step.action, (step.next_state.state.on_hand,step.next_state.state.on_order), step.reward) for step in step_lst]
# list_of_tuples
states, actions, next_states, rewards = [list(tup) for tup in zip(*list_of_tuples)]
cum_reward_pol_2 = np.cumsum(rewards)

3.5.3 Deterministic Policy with Reorder Point set to Midpoint (Midpoint Inventory)

\(\theta = \text{max}(r - (\alpha + \beta), 0)\)

where: - \(\theta \in \mathbb Z_{\ge0}\) is the order quantity - \(r \in \mathbb Z_{\ge0}\) is the reorder point below which reordering is allowed. - \(\alpha\) is the on-hand inventory - \(\beta\) is the on-order inventory - \((\alpha,\beta)\) is the state

We set \(r = \frac{C}{2}\).

reorder_point_pol_3 = capacity//2; reorder_point_pol_3
2
pol_3 = SimpleInventoryDeterministicPolicy(reorder_point=reorder_point_pol_3); pol_3
SimpleInventoryDeterministicPolicy(action_for=<function SimpleInventoryDeterministicPolicy.__init__.<locals>.action_for at 0x7fcccc7e90e0>)
step_gen = si_mdp.simulate_action(
    start_state_distribution=ssd, 
    policy=pol_3) 
step_lst = list(itertools.islice(step_gen, n_steps))
pprint(step_lst[:5])
[TransitionStep(state=NonTerminal(state=InventoryState(on_hand=1, on_order=3)), action=0, next_state=NonTerminal(state=InventoryState(on_hand=4, on_order=0)), reward=-1.0),
 TransitionStep(state=NonTerminal(state=InventoryState(on_hand=4, on_order=0)), action=0, next_state=NonTerminal(state=InventoryState(on_hand=4, on_order=0)), reward=-4.0),
 TransitionStep(state=NonTerminal(state=InventoryState(on_hand=4, on_order=0)), action=0, next_state=NonTerminal(state=InventoryState(on_hand=3, on_order=0)), reward=-4.0),
 TransitionStep(state=NonTerminal(state=InventoryState(on_hand=3, on_order=0)), action=0, next_state=NonTerminal(state=InventoryState(on_hand=2, on_order=0)), reward=-3.0),
 TransitionStep(state=NonTerminal(state=InventoryState(on_hand=2, on_order=0)), action=0, next_state=NonTerminal(state=InventoryState(on_hand=1, on_order=0)), reward=-2.0)]
list_of_tuples = [((step.state.state.on_hand,step.state.state.on_order), step.action, (step.next_state.state.on_hand,step.next_state.state.on_order), step.reward) for step in step_lst]
# list_of_tuples
states, actions, next_states, rewards = [list(tup) for tup in zip(*list_of_tuples)]
cum_reward_pol_3 = np.cumsum(rewards)

3.5.4 Optimal Policy (TD Q-Learning)

print(f"TD (Q-Learning) Optimal Policy with {n_updates:d} updates")
pprint(opt_pol)
TD (Q-Learning) Optimal Policy with 1000000 updates
For State InventoryState(on_hand=0, on_order=0): Do Action 2
For State InventoryState(on_hand=0, on_order=1): Do Action 2
For State InventoryState(on_hand=0, on_order=2): Do Action 1
For State InventoryState(on_hand=0, on_order=3): Do Action 1
For State InventoryState(on_hand=0, on_order=4): Do Action 0
For State InventoryState(on_hand=0, on_order=5): Do Action 0
For State InventoryState(on_hand=1, on_order=0): Do Action 2
For State InventoryState(on_hand=1, on_order=1): Do Action 1
For State InventoryState(on_hand=1, on_order=2): Do Action 1
For State InventoryState(on_hand=1, on_order=3): Do Action 0
For State InventoryState(on_hand=1, on_order=4): Do Action 0
For State InventoryState(on_hand=2, on_order=0): Do Action 1
For State InventoryState(on_hand=2, on_order=1): Do Action 1
For State InventoryState(on_hand=2, on_order=2): Do Action 0
For State InventoryState(on_hand=2, on_order=3): Do Action 0
For State InventoryState(on_hand=3, on_order=0): Do Action 1
For State InventoryState(on_hand=3, on_order=1): Do Action 0
For State InventoryState(on_hand=3, on_order=2): Do Action 0
For State InventoryState(on_hand=4, on_order=0): Do Action 0
For State InventoryState(on_hand=4, on_order=1): Do Action 0
For State InventoryState(on_hand=5, on_order=0): Do Action 0

type(opt_pol)
rl.policy_ANNO.FiniteDeterministicPolicy
step_gen = si_mdp.simulate_action(
    start_state_distribution=ssd, 
    policy=opt_pol) 
step_lst = list(itertools.islice(step_gen, n_steps))
pprint(step_lst[:5])
[TransitionStep(state=NonTerminal(state=InventoryState(on_hand=0, on_order=2)), action=1, next_state=NonTerminal(state=InventoryState(on_hand=2, on_order=1)), reward=-0.0),
 TransitionStep(state=NonTerminal(state=InventoryState(on_hand=2, on_order=1)), action=1, next_state=NonTerminal(state=InventoryState(on_hand=3, on_order=1)), reward=-2.0),
 TransitionStep(state=NonTerminal(state=InventoryState(on_hand=3, on_order=1)), action=0, next_state=NonTerminal(state=InventoryState(on_hand=4, on_order=0)), reward=-3.0),
 TransitionStep(state=NonTerminal(state=InventoryState(on_hand=4, on_order=0)), action=0, next_state=NonTerminal(state=InventoryState(on_hand=2, on_order=0)), reward=-4.0),
 TransitionStep(state=NonTerminal(state=InventoryState(on_hand=2, on_order=0)), action=1, next_state=NonTerminal(state=InventoryState(on_hand=1, on_order=1)), reward=-2.0)]
list_of_tuples = [((step.state.state.on_hand,step.state.state.on_order), step.action, (step.next_state.state.on_hand,step.next_state.state.on_order), step.reward) for step in step_lst]
# list_of_tuples
states, actions, next_states, rewards = [list(tup) for tup in zip(*list_of_tuples)]
cum_reward_pol_opt = np.cumsum(rewards)

3.5.5 True Optimal Policy

print(f"TD (Q-Learning) True Optimal Policy with {n_updates:d} updates")
pprint(true_opt_pol)
TD (Q-Learning) True Optimal Policy with 1000000 updates
For State InventoryState(on_hand=0, on_order=0): Do Action 2
For State InventoryState(on_hand=0, on_order=1): Do Action 2
For State InventoryState(on_hand=0, on_order=2): Do Action 1
For State InventoryState(on_hand=0, on_order=3): Do Action 1
For State InventoryState(on_hand=0, on_order=4): Do Action 0
For State InventoryState(on_hand=0, on_order=5): Do Action 0
For State InventoryState(on_hand=1, on_order=0): Do Action 2
For State InventoryState(on_hand=1, on_order=1): Do Action 1
For State InventoryState(on_hand=1, on_order=2): Do Action 1
For State InventoryState(on_hand=1, on_order=3): Do Action 0
For State InventoryState(on_hand=1, on_order=4): Do Action 0
For State InventoryState(on_hand=2, on_order=0): Do Action 1
For State InventoryState(on_hand=2, on_order=1): Do Action 1
For State InventoryState(on_hand=2, on_order=2): Do Action 0
For State InventoryState(on_hand=2, on_order=3): Do Action 0
For State InventoryState(on_hand=3, on_order=0): Do Action 1
For State InventoryState(on_hand=3, on_order=1): Do Action 0
For State InventoryState(on_hand=3, on_order=2): Do Action 0
For State InventoryState(on_hand=4, on_order=0): Do Action 0
For State InventoryState(on_hand=4, on_order=1): Do Action 0
For State InventoryState(on_hand=5, on_order=0): Do Action 0

step_gen = si_mdp.simulate_action(
    start_state_distribution=ssd, 
    policy=true_opt_pol)
step_lst = list(itertools.islice(step_gen, n_steps))
pprint(step_lst[:5])
[TransitionStep(state=NonTerminal(state=InventoryState(on_hand=2, on_order=1)), action=1, next_state=NonTerminal(state=InventoryState(on_hand=1, on_order=1)), reward=-2.0),
 TransitionStep(state=NonTerminal(state=InventoryState(on_hand=1, on_order=1)), action=1, next_state=NonTerminal(state=InventoryState(on_hand=1, on_order=1)), reward=-1.0),
 TransitionStep(state=NonTerminal(state=InventoryState(on_hand=1, on_order=1)), action=1, next_state=NonTerminal(state=InventoryState(on_hand=2, on_order=1)), reward=-1.0),
 TransitionStep(state=NonTerminal(state=InventoryState(on_hand=2, on_order=1)), action=1, next_state=NonTerminal(state=InventoryState(on_hand=2, on_order=1)), reward=-2.0),
 TransitionStep(state=NonTerminal(state=InventoryState(on_hand=2, on_order=1)), action=1, next_state=NonTerminal(state=InventoryState(on_hand=0, on_order=1)), reward=-2.2333692644293284)]
list_of_tuples = [((step.state.state.on_hand,step.state.state.on_order), step.action, (step.next_state.state.on_hand,step.next_state.state.on_order), step.reward) for step in step_lst]
# list_of_tuples
states, actions, next_states, rewards = [list(tup) for tup in zip(*list_of_tuples)]
cum_reward_pol_opt_true = np.cumsum(rewards)

3.5.6 Visualization

label_list = ['Max Inventory', 'Min Inventory', 'Midpoint Inventory', 'Optimal (Q-Learning)', 'True Optimal']
plot_list = [cum_reward_pol_1, cum_reward_pol_2, cum_reward_pol_3, cum_reward_pol_opt, cum_reward_pol_opt_true]
fig,axs = plt.subplots(figsize=(16,15))
axs.set_xlabel('Steps', fontsize=20)
axs.set_title(f'Cumulative Reward', fontsize=24)
for i,cum_r in enumerate(plot_list):
  axs.plot(cum_r, label=label_list[i])
# axs.set_ylim([-5000,0])
axs.legend(fontsize=15);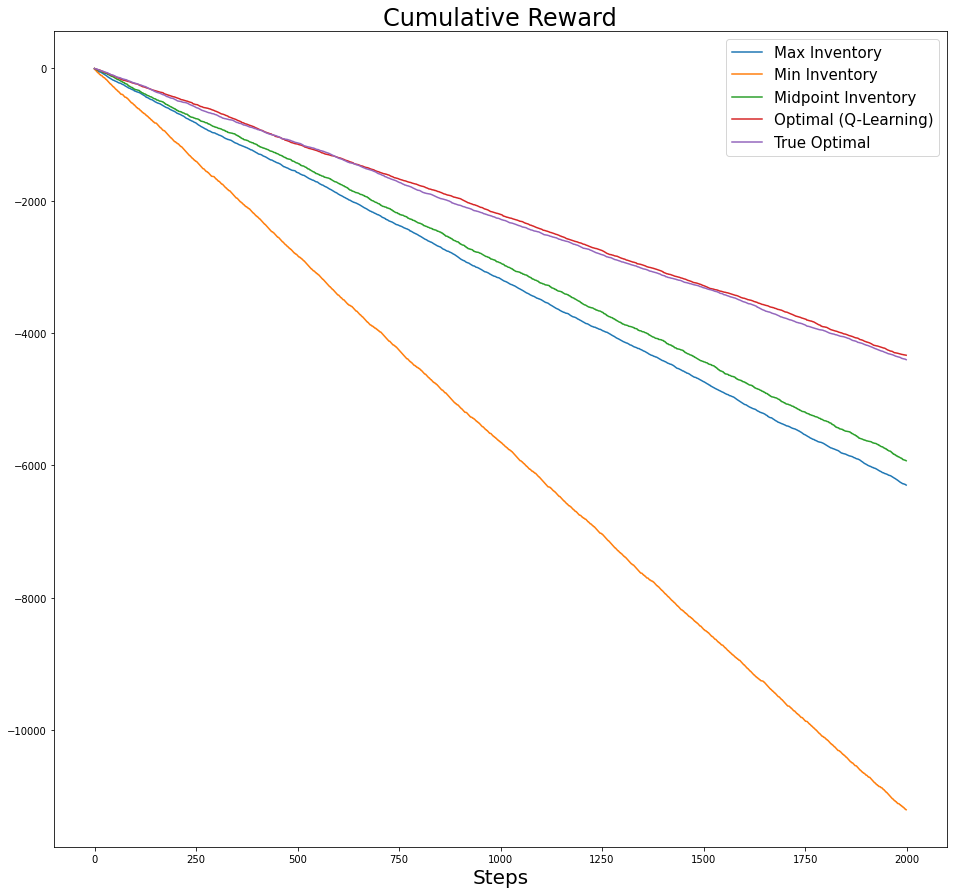

fig,axs = plt.subplots(figsize=(16,15))
axs.set_xlabel('Steps', fontsize=20)
axs.set_title(f'Cumulative Cost', fontsize=24)
for i,cum_r in enumerate(plot_list):
  axs.plot(-cum_r, label=label_list[i])
# axs.set_ylim([0, 5000])
axs.legend(fontsize=15);

Now we zoom in a bit:

fig,axs = plt.subplots(figsize=(16,15))
axs.set_xlabel('Steps', fontsize=20)
axs.set_title(f'Cumulative Reward', fontsize=24)
for i,cum_r in enumerate(plot_list):
  axs.plot(cum_r, label=label_list[i])
axs.set_ylim([-3000,0])
axs.legend(fontsize=15);

fig,axs = plt.subplots(figsize=(16,15))
axs.set_xlabel('Steps', fontsize=20)
axs.set_title(f'Cumulative Cost', fontsize=24)
for i,cum_r in enumerate(plot_list):
  axs.plot(-cum_r, label=label_list[i])
axs.set_ylim([0, 3000])
axs.legend(fontsize=15);