An RL Approach for Inventory Management (Part 10)

Tabular Temporal-Difference (SARSA) Control

Inventory Management
Markov Decision Process
TD
SARSA
Author

Kobus Esterhuysen

Published

July 21, 2022

1 Generalized Policy Iteration (GPI)

In previous projects we have only dealt with the prediction problem. In this project we move on to the control problem. We stay in the model-free or learning domain (rather than planning), i.e. making use of Reinforcement Learning algorithms. We will explore the depth of update dimension, considering both bootstrapping and non-bootstrapping methods like Temporal-Difference (TD) and Monte-Carlo (MC) algorithms respectively.

What is different about Control, rather than Prediction, is the depence on the concept of Generalized Policy Iteration (GPI).

The key concept of GPI is that we can: - Evaluate a policy with any Policy Evaluation method - Improve a policy with any Policy Improvement method

2 GPI with Evaluation as Monte-Carlo (MC)

Here is a reasonable way to approach MC Control based on what we have done so far: - do MC Policy Evaluation (which is essentially MC Prediction) - do greedy Policy Improvement - do MC Policy Evaluation on the improved policy - etc., etc.

However, this naive approach leads to some complications.

2.1 Greedy Policy Improvement requires \(\mathcal P\) and \(\mathcal R\)

The first complication is that: - Greedy Policy Improvement requires the - state transition probability function \(\mathcal P\) - reward function \(\mathcal R\) This is not available in the model-free domain. (They were, however, available in the model-based domain when we performed dynamic programming).

We address this complication by noting that

\[ \pi'_D(s) = \underset{a \in \mathcal A}{\text{arg max}} \{\mathcal R(s, a) + \gamma \sum_{s' \in \mathcal N}\mathcal P(s, a, s') \cdot V^\pi(s')\} \text{ for all } s \in \mathcal N \]

can be expressed more concisely as:

\[ \pi'_D(s) = \underset{a \in \mathcal A}{\text{arg max}} Q^\pi(s, a) \text{ for all } s \in \mathcal N \]

This is valuable because: - Instead of doing - Policy Evaluation to calculate \(V^\pi\) - We do - Policy Evaluation to calculate \(Q^\pi\) (i.e. MC Prediction for the Action Value Function, \(Q\))

2.2 Biased initial random occurrences of returns

The second complication is that updates can get biased by initial random occurrences of returns. This could prevent certain actions from being sufficiently chosen. This will lead to inaccurate estimates of the action values for those actions. We want to exploit actions that provide better returns but at the same time also be sure to explore all possible actions. This problem is known as the exploration-exploitation dilemma.

The way to address this complication is to modify our Tabular MC Control algorithm: - Instead of doing - greedy Policy Improvement - we want to do - \(\epsilon\)-greedy Policy Improvement

This impoved stochastic policy is defined as:

\[ \pi'(s, a) = \left\{ \begin{array}{ll} \frac{\epsilon}{|\mathcal A|}+1-\epsilon & \mbox{if } a= \mbox{arg max}_{b \in \mathcal A} Q(s, b) \\ \frac{\epsilon}{|\mathcal A|} & \mbox{otherwise} \end{array} \right. \]

This means the: - exploit probability is: \(1-\epsilon\) - select the action that maximizes \(Q\) for a given state - explore probability is: \(\epsilon\) - uniform-randomly select an allowable action

The deterministic greedy policy \(\pi'_D\) is a special case of the \(\epsilon\)-greedy policy \(\pi'\). This happens when \(\epsilon=0\).

!python --version
Python 3.7.15
from typing import Tuple, Callable, Sequence, Mapping, Iterator, Iterable, TypeVar, Set
import itertools
import inspect
from pprint import pprint
from operator import itemgetter

3 Temporal-Difference (TD) Control (SARSA)

3.1 TD Control with TAB (Tabular)

With FAP TD, an update is made to the parameters of the Action Value Function \(Q\) every time we transition from a state-action \((S_t, A_t)\) to state-action \((S_{t+1},A_{t+1})\) with reward \(R_{t+1}\).

Let us consider again the Action Value Function update for MC (Monte-Carlo) Control in the TAB case:

\[ Q(S_t,A_t) ← Q(S_t,A_t) + \alpha ⋅ [G_t - Q(S_t,A_t)] \]

To move from MC to TD we take advantage of the recursive structure of the Action Value Function in the MDP Bellman equation. We do this by forming an estimate for \(G_t\) from \(R_{t+1}\) and \(Q(S_{t+1},A_{t+1})\). This means the update for TAB TD Control is:

\[ Q(S_t,A_t) ← Q(S_t,A_t) + \alpha ⋅ [R_{t+1} + \gamma \cdot Q(S_{t+1},A_{t+1}) - Q(S_t,A_t)] \]

where the

  • TD Target is \(R_{t+1} + \gamma \cdot Q(S_{t+1},A_{t+1})\)
  • TD Error is \(\delta_t = R_{t+1} + \gamma \cdot Q(S_{t+1},A_{t+1}) - Q(S_t,A_t)\)

3.2 TD Control with FAP (Function Approximation)

To move from MC to TD we do the same type of replacement, i.e. we replace \(G_t\) with \(R_{t+1}+\gamma \cdot Q(S_{t+1},A_{t+1};w)\) in the expression for MC Control:

\[ \Delta w = \alpha \cdot [G_t - Q(S_t,A_t;w)] \cdot \nabla_wQ(S_t,A_t;w) \]

This leads to the parameter update:

\[ \begin{aligned} \Delta w &= \alpha \cdot [R_{t+1}+\gamma \cdot Q(S_{t+1},A_{t+1};w)-Q(S_t,A_t;w)] \cdot \nabla_w Q(S_t,A_t;w) \\ &= \alpha \cdot \delta_t \cdot \nabla_w Q(S_t,A_t;w) \end{aligned} \]

where

\[ \delta_t = R_{t+1}+\gamma \cdot Q(S_{t+1},A_{t+1};w)-Q(S_t,A_t;w) \]

3.3 Generalized implementation of GLIE Temporal_Difference (SARSA) Control

The following code can handle both TAB and FAP cases.

A = TypeVar('A')

def epsilon_greedy_action(
    q: QValueFunctionApprox[S, A],
    nt_state: NonTerminal[S],
    actions: Set[A],
    ϵ: float
) -> A:
    greedy_action: A = max(
        ((a, q((nt_state, a))) for a in actions),
        key=itemgetter(1)
    )[0]
    return Categorical(
        {a: ϵ / len(actions) +
         (1 - ϵ if a == greedy_action else 0.) for a in actions}
    ).sample()
def glie_sarsa(
    mdp: MarkovDecisionProcess[S, A],
    states: NTStateDistribution[S],
    approx_0: QValueFunctionApprox[S, A],
    γ: float,
    ϵ_as_func_of_episodes: Callable[[int], float],
    max_episode_length: int
) -> Iterator[QValueFunctionApprox[S, A]]:
    q: QValueFunctionApprox[S, A] = approx_0
    yield q
    num_episodes: int = 0
    while True:
        num_episodes += 1
        ϵ: float = ϵ_as_func_of_episodes(num_episodes)
        state: NonTerminal[S] = states.sample()
        action: A = epsilon_greedy_action(
            q=q,
            nt_state=state,
            actions=set(mdp.actions(state)),
            ϵ=ϵ
        )
        steps: int = 0
        while isinstance(state, NonTerminal) and steps < max_episode_length:
            #. next_state, reward = mdp.step(state, action).sample()
            next_state, reward = mdp.transition_action(state, action).sample() #.
            if isinstance(next_state, NonTerminal):
                next_action: A = epsilon_greedy_action(
                    q=q,
                    nt_state=next_state,
                    actions=set(mdp.actions(next_state)),
                    ϵ=ϵ
                )
                q = q.update([(
                    (state, action),
                    reward + γ * q((next_state, next_action))
                )])
                action = next_action
            else:
                q = q.update([((state, action), reward)])
            yield q
            steps += 1
            state = next_state

We run the GLIE TAB TD Control (SARSA) algorithm on the Inventory problem.

Let us set the capacity \(C=5\), but keep the other parameters as before.

# capacity: int = 2
capacity: int = 5
poisson_lambda: float = 1.0
holding_cost: float = 1.0
stockout_cost: float = 10.0
gamma: float = 0.9
si_mdp: SimpleInventoryMDPCap = SimpleInventoryMDPCap(
    capacity=capacity,
    poisson_lambda=poisson_lambda,
    holding_cost=holding_cost,
    stockout_cost=stockout_cost
)
# mc_episode_length_tol: float = 1e-5
max_episode_length: int = 100
epsilon_as_func_of_episodes: Callable[[int], float] = lambda k: k**-0.5
initial_learning_rate: float = 0.1
half_life: float = 10000.0
exponent: float = 1.0
gamma: float = 0.9
initial_qvf_dict: Mapping[Tuple[NonTerminal[InventoryState], int], float] = {
    (s, a): 0. for s in si_mdp.non_terminal_states for a in si_mdp.actions(s)
}
# initial_qvf_dict
learning_rate_func: Callable[[int], float] = learning_rate_schedule(
    initial_learning_rate=initial_learning_rate,
    half_life=half_life,
    exponent=exponent
)
qvfas: Iterator[QValueFunctionApprox[InventoryState, int]] = glie_sarsa(
    mdp=si_mdp, 
    states=Choose(si_mdp.non_terminal_states),
    approx_0=Tabular(
        values_map=initial_qvf_dict, 
        count_to_weight_func=learning_rate_func
    ), 
    γ=gamma, 
    ϵ_as_func_of_episodes=epsilon_as_func_of_episodes, 
    max_episode_length=max_episode_length
)
qvfas
<generator object glie_sarsa at 0x7f909a375750>

Now we get the final estimate of the Optimal Action-Value Function after n_episodes*max_episode_length. Then we extract from it the estimate of the Optimal State-Value Function and the Optimal Policy.

n_episodes = 10_000
n_updates = n_episodes*max_episode_length
%%time
qvfa_lst = [qvfa for qvfa in itertools.islice(qvfas, n_updates)]
CPU times: user 1min 46s, sys: 4.36 s, total: 1min 50s
Wall time: 1min 53s
final_qvfa: QValueFunctionApprox[InventoryState, int] = iterate.last(qvfa_lst)
final_qvfa
Tabular(values_map={(NonTerminal(state=InventoryState(on_hand=0, on_order=0)), 0): -32.37032518995668, (NonTerminal(state=InventoryState(on_hand=0, on_order=0)), 1): -28.11080390380002, (NonTerminal(state=InventoryState(on_hand=0, on_order=0)), 2): -26.928160077677607, (NonTerminal(state=InventoryState(on_hand=0, on_order=0)), 3): -28.089955323518332, (NonTerminal(state=InventoryState(on_hand=0, on_order=0)), 4): -28.84917370891593, (NonTerminal(state=InventoryState(on_hand=0, on_order=0)), 5): -30.34044494762847, (NonTerminal(state=InventoryState(on_hand=0, on_order=1)), 0): -22.74863141799108, (NonTerminal(state=InventoryState(on_hand=0, on_order=1)), 1): -20.431733997556083, (NonTerminal(state=InventoryState(on_hand=0, on_order=1)), 2): -19.876556017860565, (NonTerminal(state=InventoryState(on_hand=0, on_order=1)), 3): -20.71695335019422, (NonTerminal(state=InventoryState(on_hand=0, on_order=1)), 4): -22.646675995375553, (NonTerminal(state=InventoryState(on_hand=0, on_order=2)), 0): -21.6958878092199, (NonTerminal(state=InventoryState(on_hand=0, on_order=2)), 1): -18.830329199292386, (NonTerminal(state=InventoryState(on_hand=0, on_order=2)), 2): -19.391472241143543, (NonTerminal(state=InventoryState(on_hand=0, on_order=2)), 3): -20.13937822788382, (NonTerminal(state=InventoryState(on_hand=0, on_order=3)), 0): -21.16405073462699, (NonTerminal(state=InventoryState(on_hand=0, on_order=3)), 1): -20.4037465529778, (NonTerminal(state=InventoryState(on_hand=0, on_order=3)), 2): -20.942233222513543, (NonTerminal(state=InventoryState(on_hand=0, on_order=4)), 0): -21.018665342030925, (NonTerminal(state=InventoryState(on_hand=0, on_order=4)), 1): -22.38733391565681, (NonTerminal(state=InventoryState(on_hand=0, on_order=5)), 0): -23.85112125437796, (NonTerminal(state=InventoryState(on_hand=1, on_order=0)), 0): -24.801202481601678, (NonTerminal(state=InventoryState(on_hand=1, on_order=0)), 1): -21.61738316076163, (NonTerminal(state=InventoryState(on_hand=1, on_order=0)), 2): -21.119609813156657, (NonTerminal(state=InventoryState(on_hand=1, on_order=0)), 3): -22.310075857352626, (NonTerminal(state=InventoryState(on_hand=1, on_order=0)), 4): -23.40170762324093, (NonTerminal(state=InventoryState(on_hand=1, on_order=1)), 0): -21.344781003728986, (NonTerminal(state=InventoryState(on_hand=1, on_order=1)), 1): -19.965493008124675, (NonTerminal(state=InventoryState(on_hand=1, on_order=1)), 2): -20.22399723159901, (NonTerminal(state=InventoryState(on_hand=1, on_order=1)), 3): -21.706557035791235, (NonTerminal(state=InventoryState(on_hand=1, on_order=2)), 0): -21.28568498697492, (NonTerminal(state=InventoryState(on_hand=1, on_order=2)), 1): -20.813815852904373, (NonTerminal(state=InventoryState(on_hand=1, on_order=2)), 2): -21.888985971732467, (NonTerminal(state=InventoryState(on_hand=1, on_order=3)), 0): -21.686777476234663, (NonTerminal(state=InventoryState(on_hand=1, on_order=3)), 1): -23.218024055196455, (NonTerminal(state=InventoryState(on_hand=1, on_order=4)), 0): -24.59811699619161, (NonTerminal(state=InventoryState(on_hand=2, on_order=0)), 0): -22.038258091277754, (NonTerminal(state=InventoryState(on_hand=2, on_order=0)), 1): -20.88145168115964, (NonTerminal(state=InventoryState(on_hand=2, on_order=0)), 2): -21.264442778759527, (NonTerminal(state=InventoryState(on_hand=2, on_order=0)), 3): -22.754110098189333, (NonTerminal(state=InventoryState(on_hand=2, on_order=1)), 0): -22.26821779692958, (NonTerminal(state=InventoryState(on_hand=2, on_order=1)), 1): -22.064498937556117, (NonTerminal(state=InventoryState(on_hand=2, on_order=1)), 2): -22.184026187073297, (NonTerminal(state=InventoryState(on_hand=2, on_order=2)), 0): -22.626891758253834, (NonTerminal(state=InventoryState(on_hand=2, on_order=2)), 1): -24.382750397180665, (NonTerminal(state=InventoryState(on_hand=2, on_order=3)), 0): -24.057228720468245, (NonTerminal(state=InventoryState(on_hand=3, on_order=0)), 0): -23.392584265147377, (NonTerminal(state=InventoryState(on_hand=3, on_order=0)), 1): -22.84465238566573, (NonTerminal(state=InventoryState(on_hand=3, on_order=0)), 2): -23.659749318680674, (NonTerminal(state=InventoryState(on_hand=3, on_order=1)), 0): -23.90025020330217, (NonTerminal(state=InventoryState(on_hand=3, on_order=1)), 1): -24.648492880719335, (NonTerminal(state=InventoryState(on_hand=3, on_order=2)), 0): -25.259489305556105, (NonTerminal(state=InventoryState(on_hand=4, on_order=0)), 0): -24.755066564642185, (NonTerminal(state=InventoryState(on_hand=4, on_order=0)), 1): -25.697936814663322, (NonTerminal(state=InventoryState(on_hand=4, on_order=1)), 0): -26.34980006077815, (NonTerminal(state=InventoryState(on_hand=5, on_order=0)), 0): -28.09982343477371}, counts_map={(NonTerminal(state=InventoryState(on_hand=4, on_order=0)), 0): 76418, (NonTerminal(state=InventoryState(on_hand=0, on_order=0)), 1): 110, (NonTerminal(state=InventoryState(on_hand=0, on_order=1)), 4): 476, (NonTerminal(state=InventoryState(on_hand=0, on_order=4)), 1): 97, (NonTerminal(state=InventoryState(on_hand=2, on_order=1)), 2): 1696, (NonTerminal(state=InventoryState(on_hand=1, on_order=2)), 0): 5075, (NonTerminal(state=InventoryState(on_hand=3, on_order=0)), 2): 759, (NonTerminal(state=InventoryState(on_hand=2, on_order=2)), 1): 146, (NonTerminal(state=InventoryState(on_hand=4, on_order=1)), 0): 1421, (NonTerminal(state=InventoryState(on_hand=3, on_order=0)), 1): 77421, (NonTerminal(state=InventoryState(on_hand=1, on_order=4)), 0): 667, (NonTerminal(state=InventoryState(on_hand=5, on_order=0)), 0): 3833, (NonTerminal(state=InventoryState(on_hand=4, on_order=0)), 1): 1040, (NonTerminal(state=InventoryState(on_hand=0, on_order=4)), 0): 896, (NonTerminal(state=InventoryState(on_hand=2, on_order=0)), 2): 678, (NonTerminal(state=InventoryState(on_hand=2, on_order=2)), 0): 2505, (NonTerminal(state=InventoryState(on_hand=1, on_order=1)), 3): 839, (NonTerminal(state=InventoryState(on_hand=2, on_order=3)), 0): 1087, (NonTerminal(state=InventoryState(on_hand=3, on_order=1)), 0): 121304, (NonTerminal(state=InventoryState(on_hand=3, on_order=0)), 0): 6355, (NonTerminal(state=InventoryState(on_hand=1, on_order=0)), 2): 17091, (NonTerminal(state=InventoryState(on_hand=0, on_order=2)), 3): 447, (NonTerminal(state=InventoryState(on_hand=2, on_order=0)), 3): 373, (NonTerminal(state=InventoryState(on_hand=1, on_order=3)), 0): 1197, (NonTerminal(state=InventoryState(on_hand=2, on_order=0)), 0): 399, (NonTerminal(state=InventoryState(on_hand=1, on_order=0)), 1): 338, (NonTerminal(state=InventoryState(on_hand=0, on_order=1)), 2): 101465, (NonTerminal(state=InventoryState(on_hand=1, on_order=2)), 2): 440, (NonTerminal(state=InventoryState(on_hand=3, on_order=1)), 1): 1267, (NonTerminal(state=InventoryState(on_hand=1, on_order=3)), 1): 110, (NonTerminal(state=InventoryState(on_hand=1, on_order=1)), 1): 165105, (NonTerminal(state=InventoryState(on_hand=2, on_order=1)), 1): 214859, (NonTerminal(state=InventoryState(on_hand=1, on_order=0)), 0): 135, (NonTerminal(state=InventoryState(on_hand=0, on_order=2)), 0): 446, (NonTerminal(state=InventoryState(on_hand=0, on_order=0)), 3): 112, (NonTerminal(state=InventoryState(on_hand=0, on_order=3)), 1): 949, (NonTerminal(state=InventoryState(on_hand=2, on_order=1)), 0): 11817, (NonTerminal(state=InventoryState(on_hand=3, on_order=2)), 0): 1568, (NonTerminal(state=InventoryState(on_hand=1, on_order=0)), 4): 165, (NonTerminal(state=InventoryState(on_hand=0, on_order=2)), 1): 80453, (NonTerminal(state=InventoryState(on_hand=1, on_order=1)), 0): 867, (NonTerminal(state=InventoryState(on_hand=0, on_order=0)), 0): 45, (NonTerminal(state=InventoryState(on_hand=0, on_order=3)), 2): 90, (NonTerminal(state=InventoryState(on_hand=0, on_order=1)), 3): 535, (NonTerminal(state=InventoryState(on_hand=1, on_order=1)), 2): 1304, (NonTerminal(state=InventoryState(on_hand=1, on_order=2)), 1): 39684, (NonTerminal(state=InventoryState(on_hand=2, on_order=0)), 1): 45738, (NonTerminal(state=InventoryState(on_hand=0, on_order=0)), 2): 6542, (NonTerminal(state=InventoryState(on_hand=0, on_order=1)), 0): 397, (NonTerminal(state=InventoryState(on_hand=1, on_order=0)), 3): 197, (NonTerminal(state=InventoryState(on_hand=0, on_order=0)), 4): 94, (NonTerminal(state=InventoryState(on_hand=0, on_order=3)), 0): 446, (NonTerminal(state=InventoryState(on_hand=0, on_order=2)), 2): 975, (NonTerminal(state=InventoryState(on_hand=0, on_order=0)), 5): 78, (NonTerminal(state=InventoryState(on_hand=0, on_order=5)), 0): 574, (NonTerminal(state=InventoryState(on_hand=0, on_order=1)), 1): 874}, count_to_weight_func=<function learning_rate_schedule.<locals>.lr_func at 0x7f908adefa70>)
def get_vf_and_policy_from_qvf(
    mdp: FiniteMarkovDecisionProcess[S, A],
    qvf: QValueFunctionApprox[S, A]
) -> Tuple[V[S], FiniteDeterministicPolicy[S, A]]:
    opt_vf: V[S] = {
        s: max(qvf((s, a)) for a in mdp.actions(s))
        for s in mdp.non_terminal_states
    }
    opt_policy: FiniteDeterministicPolicy[S, A] = \
        FiniteDeterministicPolicy({
            s.state: qvf.argmax((s, a) for a in mdp.actions(s))[1]
            for s in mdp.non_terminal_states
        })
    return opt_vf, opt_policy
opt_svf, opt_pol = get_vf_and_policy_from_qvf(
    mdp=si_mdp,
    qvf=final_qvfa
)
print(f"GLIE TD (SARSA) Optimal Value Function with {n_updates:d} updates")
pprint(opt_svf)
GLIE TD (SARSA) Optimal Value Function with 1000000 updates
{NonTerminal(state=InventoryState(on_hand=0, on_order=0)): -26.928160077677607,
 NonTerminal(state=InventoryState(on_hand=0, on_order=1)): -19.876556017860565,
 NonTerminal(state=InventoryState(on_hand=0, on_order=2)): -18.830329199292386,
 NonTerminal(state=InventoryState(on_hand=0, on_order=3)): -20.4037465529778,
 NonTerminal(state=InventoryState(on_hand=0, on_order=4)): -21.018665342030925,
 NonTerminal(state=InventoryState(on_hand=0, on_order=5)): -23.85112125437796,
 NonTerminal(state=InventoryState(on_hand=1, on_order=0)): -21.119609813156657,
 NonTerminal(state=InventoryState(on_hand=1, on_order=1)): -19.965493008124675,
 NonTerminal(state=InventoryState(on_hand=1, on_order=2)): -20.813815852904373,
 NonTerminal(state=InventoryState(on_hand=1, on_order=3)): -21.686777476234663,
 NonTerminal(state=InventoryState(on_hand=1, on_order=4)): -24.59811699619161,
 NonTerminal(state=InventoryState(on_hand=2, on_order=0)): -20.88145168115964,
 NonTerminal(state=InventoryState(on_hand=2, on_order=1)): -22.064498937556117,
 NonTerminal(state=InventoryState(on_hand=2, on_order=2)): -22.626891758253834,
 NonTerminal(state=InventoryState(on_hand=2, on_order=3)): -24.057228720468245,
 NonTerminal(state=InventoryState(on_hand=3, on_order=0)): -22.84465238566573,
 NonTerminal(state=InventoryState(on_hand=3, on_order=1)): -23.90025020330217,
 NonTerminal(state=InventoryState(on_hand=3, on_order=2)): -25.259489305556105,
 NonTerminal(state=InventoryState(on_hand=4, on_order=0)): -24.755066564642185,
 NonTerminal(state=InventoryState(on_hand=4, on_order=1)): -26.34980006077815,
 NonTerminal(state=InventoryState(on_hand=5, on_order=0)): -28.09982343477371}
print(f"GLIE TD (SARSA) Optimal Policy with {n_updates:d} updates")
pprint(opt_pol)
GLIE TD (SARSA) Optimal Policy with 1000000 updates
For State InventoryState(on_hand=0, on_order=0): Do Action 2
For State InventoryState(on_hand=0, on_order=1): Do Action 2
For State InventoryState(on_hand=0, on_order=2): Do Action 1
For State InventoryState(on_hand=0, on_order=3): Do Action 1
For State InventoryState(on_hand=0, on_order=4): Do Action 0
For State InventoryState(on_hand=0, on_order=5): Do Action 0
For State InventoryState(on_hand=1, on_order=0): Do Action 2
For State InventoryState(on_hand=1, on_order=1): Do Action 1
For State InventoryState(on_hand=1, on_order=2): Do Action 1
For State InventoryState(on_hand=1, on_order=3): Do Action 0
For State InventoryState(on_hand=1, on_order=4): Do Action 0
For State InventoryState(on_hand=2, on_order=0): Do Action 1
For State InventoryState(on_hand=2, on_order=1): Do Action 1
For State InventoryState(on_hand=2, on_order=2): Do Action 0
For State InventoryState(on_hand=2, on_order=3): Do Action 0
For State InventoryState(on_hand=3, on_order=0): Do Action 1
For State InventoryState(on_hand=3, on_order=1): Do Action 0
For State InventoryState(on_hand=3, on_order=2): Do Action 0
For State InventoryState(on_hand=4, on_order=0): Do Action 0
For State InventoryState(on_hand=4, on_order=1): Do Action 0
For State InventoryState(on_hand=5, on_order=0): Do Action 0

For comparison, we run a Value Iteration to find the true Optimal Value Function and Optimal Policy.

true_opt_svf, true_opt_pol = value_iteration_result(mdp=si_mdp, gamma=gamma)
print("True Optimal State Value Function")
pprint(true_opt_svf)
True Optimal State Value Function
{NonTerminal(state=InventoryState(on_hand=0, on_order=0)): -26.98163492786722,
 NonTerminal(state=InventoryState(on_hand=0, on_order=1)): -19.9909558006178,
 NonTerminal(state=InventoryState(on_hand=0, on_order=2)): -18.86849301795165,
 NonTerminal(state=InventoryState(on_hand=0, on_order=3)): -19.934022635857023,
 NonTerminal(state=InventoryState(on_hand=0, on_order=4)): -20.91848526863397,
 NonTerminal(state=InventoryState(on_hand=0, on_order=5)): -22.77205311116058,
 NonTerminal(state=InventoryState(on_hand=1, on_order=0)): -20.9909558006178,
 NonTerminal(state=InventoryState(on_hand=1, on_order=1)): -19.86849301795165,
 NonTerminal(state=InventoryState(on_hand=1, on_order=2)): -20.934022635857026,
 NonTerminal(state=InventoryState(on_hand=1, on_order=3)): -21.918485268633972,
 NonTerminal(state=InventoryState(on_hand=1, on_order=4)): -23.77205311116058,
 NonTerminal(state=InventoryState(on_hand=2, on_order=0)): -20.86849301795165,
 NonTerminal(state=InventoryState(on_hand=2, on_order=1)): -21.934022635857023,
 NonTerminal(state=InventoryState(on_hand=2, on_order=2)): -22.91848526863397,
 NonTerminal(state=InventoryState(on_hand=2, on_order=3)): -24.77205311116058,
 NonTerminal(state=InventoryState(on_hand=3, on_order=0)): -22.934022635857026,
 NonTerminal(state=InventoryState(on_hand=3, on_order=1)): -23.918485268633972,
 NonTerminal(state=InventoryState(on_hand=3, on_order=2)): -25.772053111160584,
 NonTerminal(state=InventoryState(on_hand=4, on_order=0)): -24.91848526863397,
 NonTerminal(state=InventoryState(on_hand=4, on_order=1)): -26.772053111160577,
 NonTerminal(state=InventoryState(on_hand=5, on_order=0)): -27.772053111160577}
print("True Optimal Policy")
pprint(true_opt_pol)
True Optimal Policy
For State InventoryState(on_hand=0, on_order=0): Do Action 2
For State InventoryState(on_hand=0, on_order=1): Do Action 2
For State InventoryState(on_hand=0, on_order=2): Do Action 1
For State InventoryState(on_hand=0, on_order=3): Do Action 1
For State InventoryState(on_hand=0, on_order=4): Do Action 0
For State InventoryState(on_hand=0, on_order=5): Do Action 0
For State InventoryState(on_hand=1, on_order=0): Do Action 2
For State InventoryState(on_hand=1, on_order=1): Do Action 1
For State InventoryState(on_hand=1, on_order=2): Do Action 1
For State InventoryState(on_hand=1, on_order=3): Do Action 0
For State InventoryState(on_hand=1, on_order=4): Do Action 0
For State InventoryState(on_hand=2, on_order=0): Do Action 1
For State InventoryState(on_hand=2, on_order=1): Do Action 1
For State InventoryState(on_hand=2, on_order=2): Do Action 0
For State InventoryState(on_hand=2, on_order=3): Do Action 0
For State InventoryState(on_hand=3, on_order=0): Do Action 1
For State InventoryState(on_hand=3, on_order=1): Do Action 0
For State InventoryState(on_hand=3, on_order=2): Do Action 0
For State InventoryState(on_hand=4, on_order=0): Do Action 0
For State InventoryState(on_hand=4, on_order=1): Do Action 0
For State InventoryState(on_hand=5, on_order=0): Do Action 0

Now we compare values by state for the State Value Function

[(true_opt_svf[s], opt_svf[s]) for s in si_mdp.non_terminal_states]
[(-26.98163492786722, -26.928160077677607),
 (-19.9909558006178, -19.876556017860565),
 (-18.86849301795165, -18.830329199292386),
 (-19.934022635857023, -20.4037465529778),
 (-20.91848526863397, -21.018665342030925),
 (-22.77205311116058, -23.85112125437796),
 (-20.9909558006178, -21.119609813156657),
 (-19.86849301795165, -19.965493008124675),
 (-20.934022635857026, -20.813815852904373),
 (-21.918485268633972, -21.686777476234663),
 (-23.77205311116058, -24.59811699619161),
 (-20.86849301795165, -20.88145168115964),
 (-21.934022635857023, -22.064498937556117),
 (-22.91848526863397, -22.626891758253834),
 (-24.77205311116058, -24.057228720468245),
 (-22.934022635857026, -22.84465238566573),
 (-23.918485268633972, -23.90025020330217),
 (-25.772053111160584, -25.259489305556105),
 (-24.91848526863397, -24.755066564642185),
 (-26.772053111160577, -26.34980006077815),
 (-27.772053111160577, -28.09982343477371)]

We also compare values by state for the Policy

[(true_opt_pol.policy_map[s.state], opt_pol.policy_map[s.state]) for s in si_mdp.non_terminal_states]
[(Constant(value=2), Constant(value=2)),
 (Constant(value=2), Constant(value=2)),
 (Constant(value=1), Constant(value=1)),
 (Constant(value=1), Constant(value=1)),
 (Constant(value=0), Constant(value=0)),
 (Constant(value=0), Constant(value=0)),
 (Constant(value=2), Constant(value=2)),
 (Constant(value=1), Constant(value=1)),
 (Constant(value=1), Constant(value=1)),
 (Constant(value=0), Constant(value=0)),
 (Constant(value=0), Constant(value=0)),
 (Constant(value=1), Constant(value=1)),
 (Constant(value=1), Constant(value=1)),
 (Constant(value=0), Constant(value=0)),
 (Constant(value=0), Constant(value=0)),
 (Constant(value=1), Constant(value=1)),
 (Constant(value=0), Constant(value=0)),
 (Constant(value=0), Constant(value=0)),
 (Constant(value=0), Constant(value=0)),
 (Constant(value=0), Constant(value=0)),
 (Constant(value=0), Constant(value=0))]

3.4 Visualize

Let us visualize the convergence of the Action Value Function (Q) for each of the states:

qvfa_lst[10]
Tabular(values_map={(NonTerminal(state=InventoryState(on_hand=0, on_order=0)), 0): 0.0, (NonTerminal(state=InventoryState(on_hand=0, on_order=0)), 1): -1.0, (NonTerminal(state=InventoryState(on_hand=0, on_order=0)), 2): 0.0, (NonTerminal(state=InventoryState(on_hand=0, on_order=0)), 3): 0.0, (NonTerminal(state=InventoryState(on_hand=0, on_order=0)), 4): 0.0, (NonTerminal(state=InventoryState(on_hand=0, on_order=0)), 5): 0.0, (NonTerminal(state=InventoryState(on_hand=0, on_order=1)), 0): 0.0, (NonTerminal(state=InventoryState(on_hand=0, on_order=1)), 1): 0.0, (NonTerminal(state=InventoryState(on_hand=0, on_order=1)), 2): 0.0, (NonTerminal(state=InventoryState(on_hand=0, on_order=1)), 3): 0.0, (NonTerminal(state=InventoryState(on_hand=0, on_order=1)), 4): -0.36787944117144233, (NonTerminal(state=InventoryState(on_hand=0, on_order=2)), 0): 0.0, (NonTerminal(state=InventoryState(on_hand=0, on_order=2)), 1): 0.0, (NonTerminal(state=InventoryState(on_hand=0, on_order=2)), 2): 0.0, (NonTerminal(state=InventoryState(on_hand=0, on_order=2)), 3): 0.0, (NonTerminal(state=InventoryState(on_hand=0, on_order=3)), 0): 0.0, (NonTerminal(state=InventoryState(on_hand=0, on_order=3)), 1): 0.0, (NonTerminal(state=InventoryState(on_hand=0, on_order=3)), 2): 0.0, (NonTerminal(state=InventoryState(on_hand=0, on_order=4)), 0): 0.0, (NonTerminal(state=InventoryState(on_hand=0, on_order=4)), 1): 0.0, (NonTerminal(state=InventoryState(on_hand=0, on_order=5)), 0): 0.0, (NonTerminal(state=InventoryState(on_hand=1, on_order=0)), 0): 0.0, (NonTerminal(state=InventoryState(on_hand=1, on_order=0)), 1): 0.0, (NonTerminal(state=InventoryState(on_hand=1, on_order=0)), 2): 0.0, (NonTerminal(state=InventoryState(on_hand=1, on_order=0)), 3): 0.0, (NonTerminal(state=InventoryState(on_hand=1, on_order=0)), 4): 0.0, (NonTerminal(state=InventoryState(on_hand=1, on_order=1)), 0): 0.0, (NonTerminal(state=InventoryState(on_hand=1, on_order=1)), 1): 0.0, (NonTerminal(state=InventoryState(on_hand=1, on_order=1)), 2): 0.0, (NonTerminal(state=InventoryState(on_hand=1, on_order=1)), 3): 0.0, (NonTerminal(state=InventoryState(on_hand=1, on_order=2)), 0): -0.1, (NonTerminal(state=InventoryState(on_hand=1, on_order=2)), 1): 0.0, (NonTerminal(state=InventoryState(on_hand=1, on_order=2)), 2): 0.0, (NonTerminal(state=InventoryState(on_hand=1, on_order=3)), 0): 0.0, (NonTerminal(state=InventoryState(on_hand=1, on_order=3)), 1): 0.0, (NonTerminal(state=InventoryState(on_hand=1, on_order=4)), 0): 0.0, (NonTerminal(state=InventoryState(on_hand=2, on_order=0)), 0): 0.0, (NonTerminal(state=InventoryState(on_hand=2, on_order=0)), 1): 0.0, (NonTerminal(state=InventoryState(on_hand=2, on_order=0)), 2): 0.0, (NonTerminal(state=InventoryState(on_hand=2, on_order=0)), 3): 0.0, (NonTerminal(state=InventoryState(on_hand=2, on_order=1)), 0): 0.0, (NonTerminal(state=InventoryState(on_hand=2, on_order=1)), 1): 0.0, (NonTerminal(state=InventoryState(on_hand=2, on_order=1)), 2): -0.2, (NonTerminal(state=InventoryState(on_hand=2, on_order=2)), 0): 0.0, (NonTerminal(state=InventoryState(on_hand=2, on_order=2)), 1): -0.2, (NonTerminal(state=InventoryState(on_hand=2, on_order=3)), 0): 0.0, (NonTerminal(state=InventoryState(on_hand=3, on_order=0)), 0): 0.0, (NonTerminal(state=InventoryState(on_hand=3, on_order=0)), 1): -0.35644607614836266, (NonTerminal(state=InventoryState(on_hand=3, on_order=0)), 2): -0.30000000000000004, (NonTerminal(state=InventoryState(on_hand=3, on_order=1)), 0): 0.0, (NonTerminal(state=InventoryState(on_hand=3, on_order=1)), 1): 0.0, (NonTerminal(state=InventoryState(on_hand=3, on_order=2)), 0): 0.0, (NonTerminal(state=InventoryState(on_hand=4, on_order=0)), 0): -0.4043487695667789, (NonTerminal(state=InventoryState(on_hand=4, on_order=0)), 1): 0.0, (NonTerminal(state=InventoryState(on_hand=4, on_order=1)), 0): -0.4, (NonTerminal(state=InventoryState(on_hand=5, on_order=0)), 0): 0.0}, counts_map={(NonTerminal(state=InventoryState(on_hand=4, on_order=0)), 0): 1, (NonTerminal(state=InventoryState(on_hand=0, on_order=0)), 1): 1, (NonTerminal(state=InventoryState(on_hand=0, on_order=1)), 4): 1, (NonTerminal(state=InventoryState(on_hand=0, on_order=4)), 1): 1, (NonTerminal(state=InventoryState(on_hand=2, on_order=1)), 2): 1, (NonTerminal(state=InventoryState(on_hand=1, on_order=2)), 0): 1, (NonTerminal(state=InventoryState(on_hand=3, on_order=0)), 2): 1, (NonTerminal(state=InventoryState(on_hand=2, on_order=2)), 1): 1, (NonTerminal(state=InventoryState(on_hand=4, on_order=1)), 0): 1, (NonTerminal(state=InventoryState(on_hand=3, on_order=0)), 1): 1}, count_to_weight_func=<function learning_rate_schedule.<locals>.lr_func at 0x7f908adefa70>)
qvfa_lst[10].values_map
{(NonTerminal(state=InventoryState(on_hand=0, on_order=0)), 0): 0.0,
 (NonTerminal(state=InventoryState(on_hand=0, on_order=0)), 1): -1.0,
 (NonTerminal(state=InventoryState(on_hand=0, on_order=0)), 2): 0.0,
 (NonTerminal(state=InventoryState(on_hand=0, on_order=0)), 3): 0.0,
 (NonTerminal(state=InventoryState(on_hand=0, on_order=0)), 4): 0.0,
 (NonTerminal(state=InventoryState(on_hand=0, on_order=0)), 5): 0.0,
 (NonTerminal(state=InventoryState(on_hand=0, on_order=1)), 0): 0.0,
 (NonTerminal(state=InventoryState(on_hand=0, on_order=1)), 1): 0.0,
 (NonTerminal(state=InventoryState(on_hand=0, on_order=1)), 2): 0.0,
 (NonTerminal(state=InventoryState(on_hand=0, on_order=1)), 3): 0.0,
 (NonTerminal(state=InventoryState(on_hand=0, on_order=1)),
  4): -0.36787944117144233,
 (NonTerminal(state=InventoryState(on_hand=0, on_order=2)), 0): 0.0,
 (NonTerminal(state=InventoryState(on_hand=0, on_order=2)), 1): 0.0,
 (NonTerminal(state=InventoryState(on_hand=0, on_order=2)), 2): 0.0,
 (NonTerminal(state=InventoryState(on_hand=0, on_order=2)), 3): 0.0,
 (NonTerminal(state=InventoryState(on_hand=0, on_order=3)), 0): 0.0,
 (NonTerminal(state=InventoryState(on_hand=0, on_order=3)), 1): 0.0,
 (NonTerminal(state=InventoryState(on_hand=0, on_order=3)), 2): 0.0,
 (NonTerminal(state=InventoryState(on_hand=0, on_order=4)), 0): 0.0,
 (NonTerminal(state=InventoryState(on_hand=0, on_order=4)), 1): 0.0,
 (NonTerminal(state=InventoryState(on_hand=0, on_order=5)), 0): 0.0,
 (NonTerminal(state=InventoryState(on_hand=1, on_order=0)), 0): 0.0,
 (NonTerminal(state=InventoryState(on_hand=1, on_order=0)), 1): 0.0,
 (NonTerminal(state=InventoryState(on_hand=1, on_order=0)), 2): 0.0,
 (NonTerminal(state=InventoryState(on_hand=1, on_order=0)), 3): 0.0,
 (NonTerminal(state=InventoryState(on_hand=1, on_order=0)), 4): 0.0,
 (NonTerminal(state=InventoryState(on_hand=1, on_order=1)), 0): 0.0,
 (NonTerminal(state=InventoryState(on_hand=1, on_order=1)), 1): 0.0,
 (NonTerminal(state=InventoryState(on_hand=1, on_order=1)), 2): 0.0,
 (NonTerminal(state=InventoryState(on_hand=1, on_order=1)), 3): 0.0,
 (NonTerminal(state=InventoryState(on_hand=1, on_order=2)), 0): -0.1,
 (NonTerminal(state=InventoryState(on_hand=1, on_order=2)), 1): 0.0,
 (NonTerminal(state=InventoryState(on_hand=1, on_order=2)), 2): 0.0,
 (NonTerminal(state=InventoryState(on_hand=1, on_order=3)), 0): 0.0,
 (NonTerminal(state=InventoryState(on_hand=1, on_order=3)), 1): 0.0,
 (NonTerminal(state=InventoryState(on_hand=1, on_order=4)), 0): 0.0,
 (NonTerminal(state=InventoryState(on_hand=2, on_order=0)), 0): 0.0,
 (NonTerminal(state=InventoryState(on_hand=2, on_order=0)), 1): 0.0,
 (NonTerminal(state=InventoryState(on_hand=2, on_order=0)), 2): 0.0,
 (NonTerminal(state=InventoryState(on_hand=2, on_order=0)), 3): 0.0,
 (NonTerminal(state=InventoryState(on_hand=2, on_order=1)), 0): 0.0,
 (NonTerminal(state=InventoryState(on_hand=2, on_order=1)), 1): 0.0,
 (NonTerminal(state=InventoryState(on_hand=2, on_order=1)), 2): -0.2,
 (NonTerminal(state=InventoryState(on_hand=2, on_order=2)), 0): 0.0,
 (NonTerminal(state=InventoryState(on_hand=2, on_order=2)), 1): -0.2,
 (NonTerminal(state=InventoryState(on_hand=2, on_order=3)), 0): 0.0,
 (NonTerminal(state=InventoryState(on_hand=3, on_order=0)), 0): 0.0,
 (NonTerminal(state=InventoryState(on_hand=3, on_order=0)),
  1): -0.35644607614836266,
 (NonTerminal(state=InventoryState(on_hand=3, on_order=0)),
  2): -0.30000000000000004,
 (NonTerminal(state=InventoryState(on_hand=3, on_order=1)), 0): 0.0,
 (NonTerminal(state=InventoryState(on_hand=3, on_order=1)), 1): 0.0,
 (NonTerminal(state=InventoryState(on_hand=3, on_order=2)), 0): 0.0,
 (NonTerminal(state=InventoryState(on_hand=4, on_order=0)),
  0): -0.4043487695667789,
 (NonTerminal(state=InventoryState(on_hand=4, on_order=0)), 1): 0.0,
 (NonTerminal(state=InventoryState(on_hand=4, on_order=1)), 0): -0.4,
 (NonTerminal(state=InventoryState(on_hand=5, on_order=0)), 0): 0.0}
qvfa_lst[10].counts_map
{(NonTerminal(state=InventoryState(on_hand=4, on_order=0)), 0): 1,
 (NonTerminal(state=InventoryState(on_hand=0, on_order=0)), 1): 1,
 (NonTerminal(state=InventoryState(on_hand=0, on_order=1)), 4): 1,
 (NonTerminal(state=InventoryState(on_hand=0, on_order=4)), 1): 1,
 (NonTerminal(state=InventoryState(on_hand=2, on_order=1)), 2): 1,
 (NonTerminal(state=InventoryState(on_hand=1, on_order=2)), 0): 1,
 (NonTerminal(state=InventoryState(on_hand=3, on_order=0)), 2): 1,
 (NonTerminal(state=InventoryState(on_hand=2, on_order=2)), 1): 1,
 (NonTerminal(state=InventoryState(on_hand=4, on_order=1)), 0): 1,
 (NonTerminal(state=InventoryState(on_hand=3, on_order=0)), 1): 1}

Let us visualize how the Action Value Function for each (state, action) pair converges during the operation of the Monte-Carlo algorithm.

values_dicts = [(vfa.values_map) for vfa in qvfa_lst]
# values_dicts
# https://stackoverflow.com/questions/5946236/how-to-merge-dicts-collecting-values-from-matching-keys
from collections import defaultdict
ds = values_dicts
merged_dict = defaultdict(list)
for d in ds: #input dicts
    for key, value in d.items():
        merged_dict[key].append(value)
# merged_dict
len(merged_dict)
56
import matplotlib.pyplot as plt
fig,axs = plt.subplots(figsize=(13,10))
axs.set_xlabel('Iterations', fontsize=20)
axs.set_title(f'Convergence of action value functions during SARSA', fontsize=24)
for it in merged_dict.items():
  axs.plot(it[1], label=f'{it[0][0].state}, {it[0][1]}')
# axs.legend(fontsize=15);

3.5 Performance of optimal policy vs other policies

import numpy as np
print('capacity =', capacity)
print('poisson_lambda =', poisson_lambda) 
print('holding_cost =', holding_cost)
print('stockout_cost =', stockout_cost)
print('gamma =', gamma)
capacity = 5
poisson_lambda = 1.0
holding_cost = 1.0
stockout_cost = 10.0
gamma = 0.9
n_steps = 2_000 #number of simulation steps
class SimpleInventoryDeterministicPolicy(DeterministicPolicy[InventoryState, int]):
  def __init__(self, reorder_point: int):
    self.reorder_point: int = reorder_point
    def action_for(s: InventoryState) -> int:
      return max(self.reorder_point - s.inventory_position(), 0)
    super().__init__(action_for)
# 
# start state distribution
ssd = Choose(si_mdp.non_terminal_states)
# ssd

3.5.1 Deterministic Policy with Reorder Point set to Capacity (Maximum Inventory)

\(\theta = \text{max}(r - (\alpha + \beta), 0)\)

where: - \(\theta \in \mathbb Z_{\ge0}\) is the order quantity - \(r \in \mathbb Z_{\ge0}\) is the reorder point below which reordering is allowed. - \(\alpha\) is the on-hand inventory - \(\beta\) is the on-order inventory - \((\alpha,\beta)\) is the state

We set \(r = C\) where \(C\) is the inventory capacity for the item.

reorder_point_pol_1 = capacity; reorder_point_pol_1
5
pol_1 = SimpleInventoryDeterministicPolicy(reorder_point=reorder_point_pol_1); pol_1
SimpleInventoryDeterministicPolicy(action_for=<function SimpleInventoryDeterministicPolicy.__init__.<locals>.action_for at 0x7f908add1170>)
step_gen = si_mdp.simulate_action(
    start_state_distribution=ssd, 
    policy=pol_1) 
step_lst = list(itertools.islice(step_gen, n_steps))
pprint(step_lst[:5])
[TransitionStep(state=NonTerminal(state=InventoryState(on_hand=1, on_order=4)), action=0, next_state=NonTerminal(state=InventoryState(on_hand=3, on_order=0)), reward=-1.0),
 TransitionStep(state=NonTerminal(state=InventoryState(on_hand=3, on_order=0)), action=2, next_state=NonTerminal(state=InventoryState(on_hand=3, on_order=2)), reward=-3.0),
 TransitionStep(state=NonTerminal(state=InventoryState(on_hand=3, on_order=2)), action=0, next_state=NonTerminal(state=InventoryState(on_hand=4, on_order=0)), reward=-3.0),
 TransitionStep(state=NonTerminal(state=InventoryState(on_hand=4, on_order=0)), action=1, next_state=NonTerminal(state=InventoryState(on_hand=3, on_order=1)), reward=-4.0),
 TransitionStep(state=NonTerminal(state=InventoryState(on_hand=3, on_order=1)), action=1, next_state=NonTerminal(state=InventoryState(on_hand=4, on_order=1)), reward=-3.0)]
list_of_tuples = [((step.state.state.on_hand,step.state.state.on_order), step.action, (step.next_state.state.on_hand,step.next_state.state.on_order), step.reward) for step in step_lst]
# list_of_tuples
states, actions, next_states, rewards = [list(tup) for tup in zip(*list_of_tuples)]
cum_reward_pol_1 = np.cumsum(rewards)

3.5.2 Deterministic Policy with Reorder Point set to 1 (Minimum Inventory)

\(\theta = \text{max}(r - (\alpha + \beta), 0)\)

where: - \(\theta \in \mathbb Z_{\ge0}\) is the order quantity - \(r \in \mathbb Z_{\ge0}\) is the reorder point below which reordering is allowed. - \(\alpha\) is the on-hand inventory - \(\beta\) is the on-order inventory - \((\alpha,\beta)\) is the state

We set \(r = 1\).

reorder_point_pol_2 = 1; reorder_point_pol_2
1
pol_2 = SimpleInventoryDeterministicPolicy(reorder_point=reorder_point_pol_2); pol_2
SimpleInventoryDeterministicPolicy(action_for=<function SimpleInventoryDeterministicPolicy.__init__.<locals>.action_for at 0x7f909a373320>)
step_gen = si_mdp.simulate_action(
    start_state_distribution=ssd, 
    policy=pol_2) 
step_lst = list(itertools.islice(step_gen, n_steps))
pprint(step_lst[:5])
[TransitionStep(state=NonTerminal(state=InventoryState(on_hand=1, on_order=1)), action=0, next_state=NonTerminal(state=InventoryState(on_hand=0, on_order=0)), reward=-2.0363832351432696),
 TransitionStep(state=NonTerminal(state=InventoryState(on_hand=0, on_order=0)), action=1, next_state=NonTerminal(state=InventoryState(on_hand=0, on_order=1)), reward=-10.0),
 TransitionStep(state=NonTerminal(state=InventoryState(on_hand=0, on_order=1)), action=0, next_state=NonTerminal(state=InventoryState(on_hand=1, on_order=0)), reward=-0.0),
 TransitionStep(state=NonTerminal(state=InventoryState(on_hand=1, on_order=0)), action=0, next_state=NonTerminal(state=InventoryState(on_hand=0, on_order=0)), reward=-4.678794411714423),
 TransitionStep(state=NonTerminal(state=InventoryState(on_hand=0, on_order=0)), action=1, next_state=NonTerminal(state=InventoryState(on_hand=0, on_order=1)), reward=-10.0)]
list_of_tuples = [((step.state.state.on_hand,step.state.state.on_order), step.action, (step.next_state.state.on_hand,step.next_state.state.on_order), step.reward) for step in step_lst]
# list_of_tuples
states, actions, next_states, rewards = [list(tup) for tup in zip(*list_of_tuples)]
cum_reward_pol_2 = np.cumsum(rewards)

3.5.3 Deterministic Policy with Reorder Point set to Midpoint (Midpoint Inventory)

\(\theta = \text{max}(r - (\alpha + \beta), 0)\)

where: - \(\theta \in \mathbb Z_{\ge0}\) is the order quantity - \(r \in \mathbb Z_{\ge0}\) is the reorder point below which reordering is allowed. - \(\alpha\) is the on-hand inventory - \(\beta\) is the on-order inventory - \((\alpha,\beta)\) is the state

We set \(r = \frac{C}{2}\).

reorder_point_pol_3 = capacity//2; reorder_point_pol_3
2
pol_3 = SimpleInventoryDeterministicPolicy(reorder_point=reorder_point_pol_3); pol_3
SimpleInventoryDeterministicPolicy(action_for=<function SimpleInventoryDeterministicPolicy.__init__.<locals>.action_for at 0x7f908add1c20>)
step_gen = si_mdp.simulate_action(
    start_state_distribution=ssd, 
    policy=pol_3) 
step_lst = list(itertools.islice(step_gen, n_steps))
pprint(step_lst[:5])
[TransitionStep(state=NonTerminal(state=InventoryState(on_hand=0, on_order=0)), action=2, next_state=NonTerminal(state=InventoryState(on_hand=0, on_order=2)), reward=-10.0),
 TransitionStep(state=NonTerminal(state=InventoryState(on_hand=0, on_order=2)), action=0, next_state=NonTerminal(state=InventoryState(on_hand=0, on_order=0)), reward=-1.0363832351432696),
 TransitionStep(state=NonTerminal(state=InventoryState(on_hand=0, on_order=0)), action=2, next_state=NonTerminal(state=InventoryState(on_hand=0, on_order=2)), reward=-10.0),
 TransitionStep(state=NonTerminal(state=InventoryState(on_hand=0, on_order=2)), action=0, next_state=NonTerminal(state=InventoryState(on_hand=0, on_order=0)), reward=-1.0363832351432696),
 TransitionStep(state=NonTerminal(state=InventoryState(on_hand=0, on_order=0)), action=2, next_state=NonTerminal(state=InventoryState(on_hand=0, on_order=2)), reward=-10.0)]
list_of_tuples = [((step.state.state.on_hand,step.state.state.on_order), step.action, (step.next_state.state.on_hand,step.next_state.state.on_order), step.reward) for step in step_lst]
# list_of_tuples
states, actions, next_states, rewards = [list(tup) for tup in zip(*list_of_tuples)]
cum_reward_pol_3 = np.cumsum(rewards)

3.5.4 Optimal Policy (SARSA)

print(f"GLIE TD (SARSA) Optimal Policy with {n_updates:d} updates")
pprint(opt_pol)
GLIE TD (SARSA) Optimal Policy with 1000000 updates
For State InventoryState(on_hand=0, on_order=0): Do Action 2
For State InventoryState(on_hand=0, on_order=1): Do Action 2
For State InventoryState(on_hand=0, on_order=2): Do Action 1
For State InventoryState(on_hand=0, on_order=3): Do Action 1
For State InventoryState(on_hand=0, on_order=4): Do Action 0
For State InventoryState(on_hand=0, on_order=5): Do Action 0
For State InventoryState(on_hand=1, on_order=0): Do Action 2
For State InventoryState(on_hand=1, on_order=1): Do Action 1
For State InventoryState(on_hand=1, on_order=2): Do Action 1
For State InventoryState(on_hand=1, on_order=3): Do Action 0
For State InventoryState(on_hand=1, on_order=4): Do Action 0
For State InventoryState(on_hand=2, on_order=0): Do Action 1
For State InventoryState(on_hand=2, on_order=1): Do Action 1
For State InventoryState(on_hand=2, on_order=2): Do Action 0
For State InventoryState(on_hand=2, on_order=3): Do Action 0
For State InventoryState(on_hand=3, on_order=0): Do Action 1
For State InventoryState(on_hand=3, on_order=1): Do Action 0
For State InventoryState(on_hand=3, on_order=2): Do Action 0
For State InventoryState(on_hand=4, on_order=0): Do Action 0
For State InventoryState(on_hand=4, on_order=1): Do Action 0
For State InventoryState(on_hand=5, on_order=0): Do Action 0

step_gen = si_mdp.simulate_action(
    start_state_distribution=ssd, 
    policy=opt_pol) 
step_lst = list(itertools.islice(step_gen, n_steps))
pprint(step_lst[:5])
[TransitionStep(state=NonTerminal(state=InventoryState(on_hand=2, on_order=1)), action=1, next_state=NonTerminal(state=InventoryState(on_hand=2, on_order=1)), reward=-2.0),
 TransitionStep(state=NonTerminal(state=InventoryState(on_hand=2, on_order=1)), action=1, next_state=NonTerminal(state=InventoryState(on_hand=2, on_order=1)), reward=-2.0),
 TransitionStep(state=NonTerminal(state=InventoryState(on_hand=2, on_order=1)), action=1, next_state=NonTerminal(state=InventoryState(on_hand=0, on_order=1)), reward=-2.2333692644293284),
 TransitionStep(state=NonTerminal(state=InventoryState(on_hand=0, on_order=1)), action=2, next_state=NonTerminal(state=InventoryState(on_hand=0, on_order=2)), reward=-3.6787944117144233),
 TransitionStep(state=NonTerminal(state=InventoryState(on_hand=0, on_order=2)), action=1, next_state=NonTerminal(state=InventoryState(on_hand=2, on_order=1)), reward=-0.0)]
list_of_tuples = [((step.state.state.on_hand,step.state.state.on_order), step.action, (step.next_state.state.on_hand,step.next_state.state.on_order), step.reward) for step in step_lst]
# list_of_tuples
states, actions, next_states, rewards = [list(tup) for tup in zip(*list_of_tuples)]
cum_reward_pol_opt = np.cumsum(rewards)

3.5.5 True Optimal Policy

print(f"GLIE TD (SARSA) True Optimal Policy with {n_updates:d} updates")
pprint(true_opt_pol)
GLIE TD (SARSA) True Optimal Policy with 1000000 updates
For State InventoryState(on_hand=0, on_order=0): Do Action 2
For State InventoryState(on_hand=0, on_order=1): Do Action 2
For State InventoryState(on_hand=0, on_order=2): Do Action 1
For State InventoryState(on_hand=0, on_order=3): Do Action 1
For State InventoryState(on_hand=0, on_order=4): Do Action 0
For State InventoryState(on_hand=0, on_order=5): Do Action 0
For State InventoryState(on_hand=1, on_order=0): Do Action 2
For State InventoryState(on_hand=1, on_order=1): Do Action 1
For State InventoryState(on_hand=1, on_order=2): Do Action 1
For State InventoryState(on_hand=1, on_order=3): Do Action 0
For State InventoryState(on_hand=1, on_order=4): Do Action 0
For State InventoryState(on_hand=2, on_order=0): Do Action 1
For State InventoryState(on_hand=2, on_order=1): Do Action 1
For State InventoryState(on_hand=2, on_order=2): Do Action 0
For State InventoryState(on_hand=2, on_order=3): Do Action 0
For State InventoryState(on_hand=3, on_order=0): Do Action 1
For State InventoryState(on_hand=3, on_order=1): Do Action 0
For State InventoryState(on_hand=3, on_order=2): Do Action 0
For State InventoryState(on_hand=4, on_order=0): Do Action 0
For State InventoryState(on_hand=4, on_order=1): Do Action 0
For State InventoryState(on_hand=5, on_order=0): Do Action 0

step_gen = si_mdp.simulate_action(
    start_state_distribution=ssd, 
    policy=true_opt_pol)
step_lst = list(itertools.islice(step_gen, n_steps))
pprint(step_lst[:5])
[TransitionStep(state=NonTerminal(state=InventoryState(on_hand=4, on_order=1)), action=0, next_state=NonTerminal(state=InventoryState(on_hand=5, on_order=0)), reward=-4.0),
 TransitionStep(state=NonTerminal(state=InventoryState(on_hand=5, on_order=0)), action=0, next_state=NonTerminal(state=InventoryState(on_hand=2, on_order=0)), reward=-5.0),
 TransitionStep(state=NonTerminal(state=InventoryState(on_hand=2, on_order=0)), action=1, next_state=NonTerminal(state=InventoryState(on_hand=0, on_order=1)), reward=-3.0363832351432696),
 TransitionStep(state=NonTerminal(state=InventoryState(on_hand=0, on_order=1)), action=2, next_state=NonTerminal(state=InventoryState(on_hand=0, on_order=2)), reward=-3.6787944117144233),
 TransitionStep(state=NonTerminal(state=InventoryState(on_hand=0, on_order=2)), action=1, next_state=NonTerminal(state=InventoryState(on_hand=2, on_order=1)), reward=-0.0)]
list_of_tuples = [((step.state.state.on_hand,step.state.state.on_order), step.action, (step.next_state.state.on_hand,step.next_state.state.on_order), step.reward) for step in step_lst]
# list_of_tuples
states, actions, next_states, rewards = [list(tup) for tup in zip(*list_of_tuples)]
cum_reward_pol_opt_true = np.cumsum(rewards)

3.5.6 Visualization

import matplotlib.pyplot as plt
label_list = ['Max Inventory', 'Min Inventory', 'Midpoint Inventory', 'Optimal (TD SARSA)', 'True Optimal']
plot_list = [cum_reward_pol_1, cum_reward_pol_2, cum_reward_pol_3, cum_reward_pol_opt, cum_reward_pol_opt_true]
fig,axs = plt.subplots(figsize=(16,15))
axs.set_xlabel('Steps', fontsize=20)
axs.set_title(f'Cumulative Reward', fontsize=24)
for i,cum_r in enumerate(plot_list):
  axs.plot(cum_r, label=label_list[i])
# axs.set_ylim([-5000,0])
axs.legend(fontsize=15);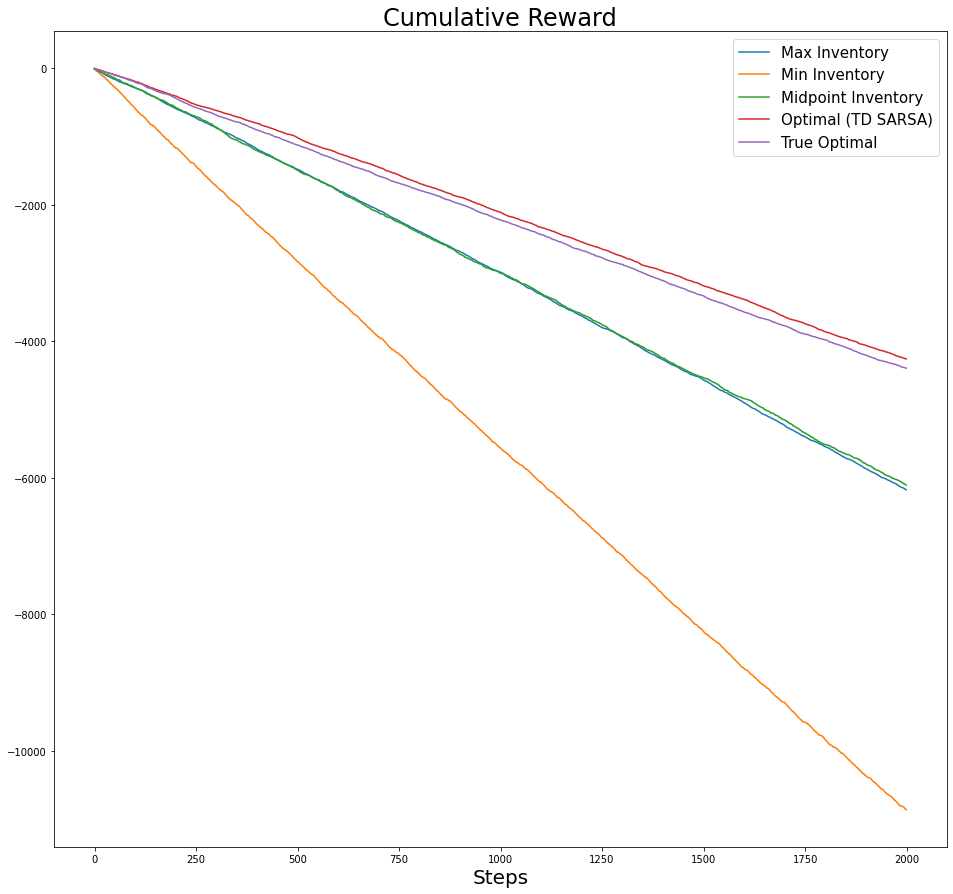

fig,axs = plt.subplots(figsize=(16,15))
axs.set_xlabel('Steps', fontsize=20)
axs.set_title(f'Cumulative Cost', fontsize=24)
for i,cum_r in enumerate(plot_list):
  axs.plot(-cum_r, label=label_list[i])
# axs.set_ylim([0, 5000])
axs.legend(fontsize=15);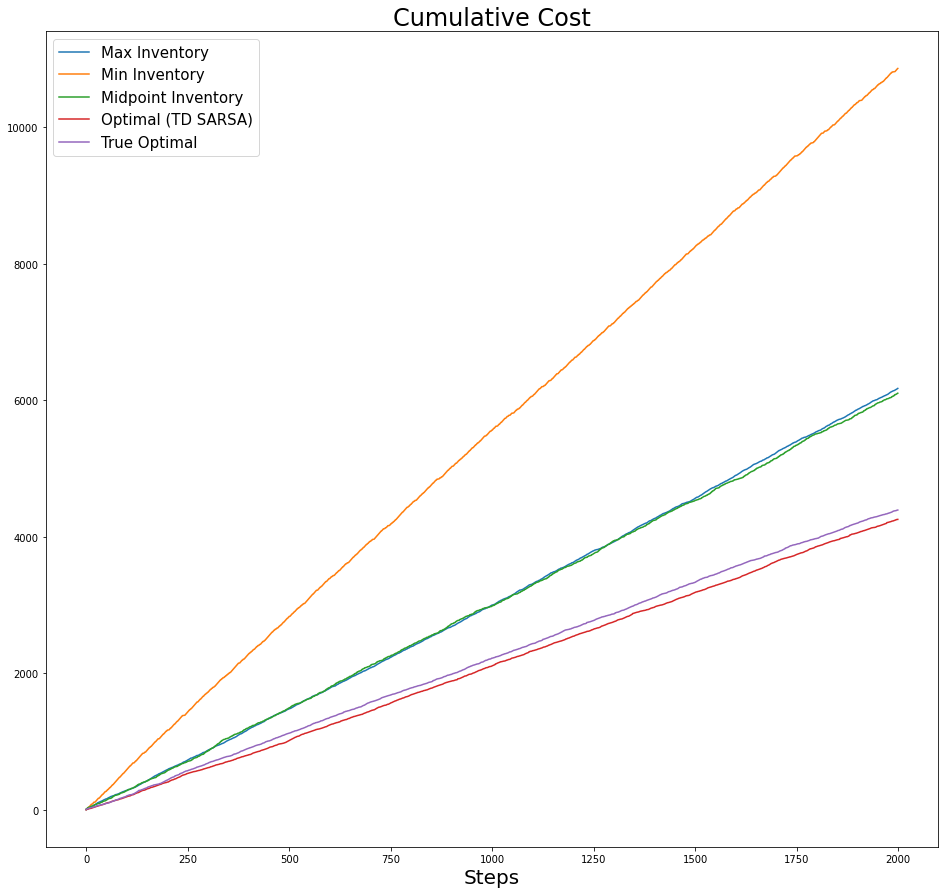

Now we zoom in a bit:

fig,axs = plt.subplots(figsize=(16,15))
axs.set_xlabel('Steps', fontsize=20)
axs.set_title(f'Cumulative Reward', fontsize=24)
for i,cum_r in enumerate(plot_list):
  axs.plot(cum_r, label=label_list[i])
axs.set_ylim([-3000,0])
axs.legend(fontsize=15);

fig,axs = plt.subplots(figsize=(16,15))
axs.set_xlabel('Steps', fontsize=20)
axs.set_title(f'Cumulative Cost', fontsize=24)
for i,cum_r in enumerate(plot_list):
  axs.plot(-cum_r, label=label_list[i])
axs.set_ylim([0, 3000])
axs.legend(fontsize=15);