Demand Simulation of a Consumer Product

Back to Portfolio of Projects | LearnableLoopAI.com | Blog |

1 BUSINESS UNDERSTANDING

In today’s highly competitive business landscape, effective marketing is crucial for any organization aiming to stand out from the crowd and attract customers. One powerful tool that marketers often employ to achieve their goals is promotions. Promotions are a key component of marketing strategies, encompassing various tactics designed to create awareness, generate interest, and drive sales for a product or service.

Promotions can take many forms, ranging from traditional methods like discounts, coupons, and contests, to modern techniques such as social media campaigns, influencer partnerships, and experiential marketing. Regardless of the specific approach, the underlying objective remains consistent: to create a compelling offer that captivates the target audience, encourages them to take action, and ultimately leads to a positive impact on the bottom line.

The strategic use of promotions provides several significant benefits to businesses. Firstly, promotions can effectively increase brand visibility and exposure. By offering discounts or running promotional campaigns, companies can attract attention from both existing and potential customers, generating buzz and curiosity around their products or services. This heightened visibility can lead to increased brand recognition and recall, helping businesses gain a competitive edge in the market.

Secondly, promotions serve as powerful incentives for customer acquisition and retention. By offering special deals or exclusive offers, companies can entice new customers to try their offerings, effectively removing barriers to entry. Additionally, promotions can reward and incentivize loyal customers, reinforcing their affinity for the brand and fostering long-term relationships. Such strategies can contribute to customer satisfaction, loyalty, and ultimately, increased customer lifetime value.

Furthermore, promotions can act as catalysts for immediate sales. By creating a sense of urgency and limited-time availability, businesses can encourage consumers to make purchasing decisions quickly. Whether it’s a flash sale, a time-limited discount, or a buy-one-get-one offer, promotions create a sense of exclusivity and value, compelling customers to act swiftly to seize the opportunity before it expires.

Moreover, promotions can be valuable tools for market research and gathering customer insights. By tracking the response and engagement generated by different promotions, companies can gain valuable data on consumer behavior, preferences, and purchasing patterns. This information can be used to refine marketing strategies, optimize product offerings, and tailor future promotions to better meet the needs and desires of the target audience.

In conclusion, promotions play a vital role in marketing, offering a range of benefits to businesses. From increasing brand visibility and attracting new customers to driving immediate sales and gathering valuable market insights, promotions are versatile tools that can significantly impact a company’s success. By carefully crafting and executing well-designed promotional campaigns, businesses can effectively engage their audience, foster brand loyalty, and achieve their marketing objectives in today’s dynamic and competitive marketplace.

2 DATA UNDERSTANDING

In the world of business, accurately forecasting demand for a product is essential for efficient production planning, inventory management, and overall business success. However, demand can often exhibit a random and unpredictable nature. To tackle this challenge, one statistical tool commonly used is the Poisson distribution, which provides a mathematical framework for simulating and analyzing random events with known average rates.

The Poisson distribution is particularly useful when modeling events that occur independently over time, such as customer arrivals, phone calls, or in our case, demand for a product. It characterizes the probability of a specific number of events occurring within a given time interval, based on the average rate at which those events typically occur. By leveraging the Poisson distribution, businesses can simulate demand patterns and make informed decisions about production levels, resource allocation, and supply chain management.

Simulating demand using the Poisson distribution involves determining the average rate or intensity of demand, typically based on historical data or industry knowledge. This rate represents the average number of product units requested per specific time period, such as per hour, per day, or per month. Once the average rate is established, the Poisson distribution can be used to generate a range of possible demand scenarios, allowing businesses to assess various outcomes and make strategic decisions accordingly.

The Poisson distribution assumes that events occur independently and at a constant average rate, making it suitable for situations where demand is influenced by random factors rather than external variables. It provides a probability distribution that assigns probabilities to different demand levels, enabling businesses to estimate the likelihood of experiencing high or low demand during a specific time period.

By using the Poisson distribution to simulate demand, businesses can gain valuable insights into the potential variability and uncertainty of customer requirements. This knowledge allows them to optimize inventory levels, determine reorder points, and fine-tune production schedules to align with anticipated demand fluctuations. Additionally, businesses can use simulated demand scenarios to evaluate the impact of different pricing strategies, promotional activities, or changes in market conditions on overall product performance.

In conclusion, the Poisson distribution is a valuable statistical tool for simulating demand in the business world. By leveraging its principles, businesses can better understand and prepare for the random nature of product demand, enabling them to make informed decisions about production, inventory, and resource allocation. With accurate demand simulations, businesses can enhance operational efficiency, minimize costs, and improve customer satisfaction, ultimately gaining a competitive edge in the marketplace.

3 DATA PREPARATION

We will use the data provided by the simulator directly. There is no need to perform additional data preparation.

The mean of a Poisson random variable is represented by $λ$ . We will work with a base $λ$ , but modify it for

Seasonality
Day of Week (DOW)
Day of Month (DOM)
The presence of concurrent promotions from competitors

The end result of the simulation is to provide us with an expected demand that is informed by these effects.

4 MODELING

4.1 Narrative

The demand $D_{t}$ for a specific product will be simulated. This demand is informed by a number of marketing related predictors. The symbol $M$ is used to stand for marketing promotion. The symbol $M$ is used rather than the symbol $P$ or $p$ which is often used for probability. A subscript $t$ is used throughout to signify that the values of the variables pertain to a specific point in time. Here are the predictors:

promotion spend (dollars), $M_{t}^{S p e n d}$
promotion start day-of-week, $M_{t}^{D O W}$
promotion start day-of-month, $M_{t}^{D O M}$
promotion current duration in days, $M_{t}^{D u r C u r}$
promotion total duration in days, $M_{t}^{D u r T o t}$
promotion duration includes a holiday (indicator), $M_{t}^{H o l}$
main competitor concurrent promotion (indicator), $M_{t}^{C o n c}$

4.2 Core Elements

This section attempts to answer three important questions: - What metrics are we going to track? - What decisions do we intend to make? - What are the sources of uncertainty?

For this problem, we are not concerned with making promotion decisions - only to simulate data. In the future we may choose to do this though. We might then be interested in the amount of profit we make after each promotion decision. The only sources of uncertainty are demand for the product and whether competitors have concurrent promotions.

4.3 Mathematical Model

We only simulate data in this project so we will not have a mathematical model of the marketing system for the purpose of “steering” it to our advantage.

4.4 Uncertainty Model

We will simulate the demand with the associated uncertainties. The variables for the simulation will be:

$D_{t}$
- the demand for the product per time interval, say per day
$M_{t}^{S p e n d}$
- promotion spend (100’s of dollars)
- values: $1. .10$
- assumptions:
  - 100 to 1000 dollars per promotion for this product
$M_{t}^{D O W}$
- promotion start day-of-week
- values: $s u n d a y . . s a t u r d a y$
$M_{t}^{D O M}$
- promotion start day-of-month
- values: $1. .30$
- assumptions:
  - this range is fine for now
$M_{t}^{D u r C u r}$
- promotion current duration in days
- values: $3. .10$
- assumtions:
  - no promotion for this product will run longer than 7 days
$M_{t}^{D u r T o t}$
- promotion total duration in days
- values: $3. .10$
- assumtions:
  - no promotion for this product will run longer than 7 days
$M_{t}^{H o l}$
- promotion duration includes a holiday (indicator)
- values: $0, 1$
$M_{t}^{C o n c}$
- main competitor concurrent promotion (indicator)
- values: $0, 1$

4.5 Implementation

# for i in range(10):
#   demands = []
#   D = simulate_demand()
#   demands.append(D)

import numpy as np

M__Spend = 0 # in $100
M__DurCur = -1 #no promotion
doy__start = 100
# n = 260 #simulate n days
n = 200 #simulate n days
lam_promotion_boost = 0
records = []
for doy in range(doy__start, doy__start + n):
  # print(f'\nNEW DAY\n=======\n{doy=}, {lam=}')
  lam = 10 #default of 10/day
  is_spring = 0
  is_summer = 0
  is_endOfYear = 0
  is_DOW = 0
  is_DOM = 0
  is_Conc = 0
  #seasonality
  # lam_seas = 0
  lam_seas = 0 + np.random.normal()
  if doy in list(range(120, 170)): #spring
      is_spring = 1
      # lam_seas = 12
      lam_seas = 12 + np.random.normal()
  elif doy in list(range(170, 280)): #summer
      is_summer = 1
      # lam_seas = 15
      lam_seas = 15 + np.random.normal()
  elif doy in list(range(320, 366)): #end of year holidays
      is_endOfYear = 1
      # lam_seas = 25
      lam_seas = 25 + np.random.normal()
  lam = lam + lam_seas
  #DOW
  lam_day_effect = 0
  if(np.random.uniform(0, 1) < 0.2): #boost for DOW
      is_DOW = 1
      # lam = lam + 10
      lam_day_effect = lam_day_effect + 10
  #DOM
  if(np.random.uniform(0, 1) < 0.1): #boost for DOM
      is_DOM = 1
      # lam = lam + 50
      lam_day_effect = lam_day_effect + 50
  lam = lam + lam_day_effect
  #CONC
  lam_conc_effect = 0
  if(np.random.uniform(0, 1) < 0.1): #suppress for CONC
      is_CONC = 1
      # lam = lam + max(0, lam - 90)
      lam_conc_effect = lam_conc_effect - 90
  lam = max(0, lam + lam_conc_effect)
  #promotion
  if(M__DurCur == -1 and np.random.uniform(0, 1) < 0.05): #start a promotion
      print(f'starting promotion on {doy=}...')
      M__DurCur = 0
      M__Spend = np.random.uniform(1, 10)
      M__DurTot = np.random.randint(3, 10)
      lam_promotion_boost = lam + M__Spend*lam
  if M__DurCur > -1: #current promotion
      M__DurCur += 1; #print(f'{M__DurCur=}')
      # lam_promotion = max(0, int(lam_promotion - 0.1*lam_promotion)); print(f'{lam_promotion=}')
      lam_promotion_boost = int(0.9*lam_promotion_boost); #print(f'{lam_promotion_boost=}')
      lam = lam + lam_promotion_boost
      # if(M__DUR > 5):
      if(M__DurCur > M__DurTot):
          M__DurCur = -1
          lam_promotion_boost = 0
          M__Spend = 0
          print(f'END OF PROMOTION')
  #find demand
  D = np.random.poisson(lam)
  records.append([doy, is_spring, is_summer, is_endOfYear, lam_seas, is_DOW, is_DOM, lam_day_effect, is_Conc, lam_conc_effect, M__DurCur, M__Spend, lam_promotion_boost, lam, D])
  # print(f'{records=}')

starting promotion on doy=106...
END OF PROMOTION
starting promotion on doy=137...
END OF PROMOTION
starting promotion on doy=178...
END OF PROMOTION
starting promotion on doy=230...
END OF PROMOTION
starting promotion on doy=255...
END OF PROMOTION

import pandas as pd
labels = ['doy', 'is_spring', 'is_summer', 'is_endOfYear', 'lam_seas', 'is_DOW', 'is_DOM', 'lam_day_effect', 'is_Conc', 'lam_conc_effect', 'M__DurCur', 'M__Spend', 'lam_promotion_boost', 'lam', 'D']
df = pd.DataFrame.from_records(data=records, columns=labels); df

	doy	is_spring	is_summer	is_endOfYear	lam_seas	is_DOW	is_DOM	lam_day_effect	is_Conc	lam_conc_effect	M__DurCur	M__Spend	lam_promotion_boost	lam	D
0	100	0	0	0	-1.020967	0	0	0	0	0	-1	0.0	0	8.979033	14
1	101	0	0	0	0.800980	0	1	50	0	0	-1	0.0	0	60.800980	53
2	102	0	0	0	1.222659	0	0	0	0	0	-1	0.0	0	11.222659	16
3	103	0	0	0	-1.033724	0	0	0	0	0	-1	0.0	0	8.966276	8
4	104	0	0	0	-0.017829	0	0	0	0	0	-1	0.0	0	9.982171	9
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
195	295	0	0	0	-0.055216	0	0	0	0	0	-1	0.0	0	9.944784	6
196	296	0	0	0	-0.973209	0	0	0	0	0	-1	0.0	0	9.026791	9
197	297	0	0	0	-0.847648	0	0	0	0	0	-1	0.0	0	9.152352	7
198	298	0	0	0	0.053806	0	0	0	0	0	-1	0.0	0	10.053806	13
199	299	0	0	0	-1.367723	1	0	10	0	0	-1	0.0	0	18.632277	26

200 rows × 15 columns

from certifi.core import where
import matplotlib.pyplot as plt
import matplotlib as mpl
def plot_output(df1, df2):
  n_charts = 6
  ylabelsize = 16
  # mpl.rcParams['lines.linewidth'] = 1.2
  fig, axs = plt.subplots(n_charts, sharex=True)
  # fig.set_figwidth(50); fig.set_figheight(10)
  fig.set_figwidth(13); fig.set_figheight(9)
  fig.suptitle('Demand Simulation', fontsize=30)

  i = 0 #seasonality
  axs[i].set_ylim(auto=True); axs[i].spines['top'].set_visible(False); axs[i].spines['right'].set_visible(True); axs[i].spines['bottom'].set_visible(False)
  axs[i].step(df1['doy'], df1['is_spring'], 'r')
  axs[i].step(df1['doy'], df1['is_summer'], 'g')
  axs[i].step(df1['doy'], df1['is_endOfYear'], 'b')
  axs[i].step(df1['doy'], df1['lam_seas'], 'k:')
  axs[i].set_ylabel('$\mathrm{is\_spring}$'+'\n'+'$\mathrm{is\_summer}$'+'\n'+'$\mathrm{is\_endOfYear}$'+'\n'+'$\lambda^{SeasEffect}$', rotation=0, ha='right', va='center', fontweight='bold', size=ylabelsize);

  i = 1 #DOW, DOM, DayEffect
  axs[i].set_ylim(auto=True); axs[i].spines['top'].set_visible(False); axs[i].spines['right'].set_visible(True); axs[i].spines['bottom'].set_visible(False)
  axs[i].step(df1['doy'], df1['is_DOW'], 'r')
  axs[i].step(df1['doy'], df1['is_DOM'], 'g')
  axs[i].step(df1['doy'], df1['lam_day_effect'], 'k:')
  axs[i].set_ylabel('$\mathrm{is\_DOW}$'+'\n'+'$\mathrm{is\_DOM}$'+'\n'+'$\lambda^{DayEffect}$', rotation=0, ha='right', va='center', fontweight='bold', size=ylabelsize);

  i = 2 #CONC, ConcEffect
  axs[i].set_ylim(auto=True); axs[i].spines['top'].set_visible(False); axs[i].spines['right'].set_visible(True); axs[i].spines['bottom'].set_visible(False)
  axs[i].step(df1['doy'], df1['is_Conc'], 'b')
  axs[i].step(df1['doy'], df1['lam_conc_effect'], 'k:')
  axs[i].set_ylabel('$\mathrm{is\_Conc}$'+'\n'+'$\lambda^{ConcEffect}$', rotation=0, ha='right', va='center', fontweight='bold', size=ylabelsize);

  i = 3 #M__DUR, M__SPEND
  axs[i].set_ylim(auto=True); axs[i].spines['top'].set_visible(False); axs[i].spines['right'].set_visible(True); axs[i].spines['bottom'].set_visible(False)
  axs[i].step(df1['doy'], df1['M__DurCur'], 'm')
  axs[i].step(df1['doy'], df1['M__Spend'], 'm:')
  axs[i].set_ylabel('$M^{DurCur}$\n$M^{Spend}$', rotation=0, ha='right', va='center', fontweight='bold', size=ylabelsize);

  i = 4 #lam_promotion_boost, lam
  axs[i].set_ylim(auto=True); axs[i].spines['top'].set_visible(False); axs[i].spines['right'].set_visible(True); axs[i].spines['bottom'].set_visible(False)
  axs[i].step(df1['doy'], df1['lam_promotion_boost'], 'k:')  
  axs[i].step(df1['doy'], df1['lam'], 'r:')
  axs[i].set_ylabel('$\lambda^{PromoEffect}$'+'\n'+'$\mathrm{\mathbb{E}}[D]$', rotation=0, ha='right', va='center', fontweight='bold', size=ylabelsize);

  i = 5 #lam, D
  axs[i].set_ylim(auto=True); axs[i].spines['top'].set_visible(False); axs[i].spines['right'].set_visible(True); axs[i].spines['bottom'].set_visible(False)
  axs[i].step(df1['doy'], df1['lam'], 'r:')
  axs[i].step(df1['doy'], df1['D'], 'r')
  axs[i].set_ylabel('$\mathrm{\mathbb{E}}[D]$\n$D}$', rotation=0, ha='right', va='center', fontweight='bold', size=ylabelsize);

  # fig.legend(labels=legendlabels, loc='center', fontsize=18)
plot_output(df, None)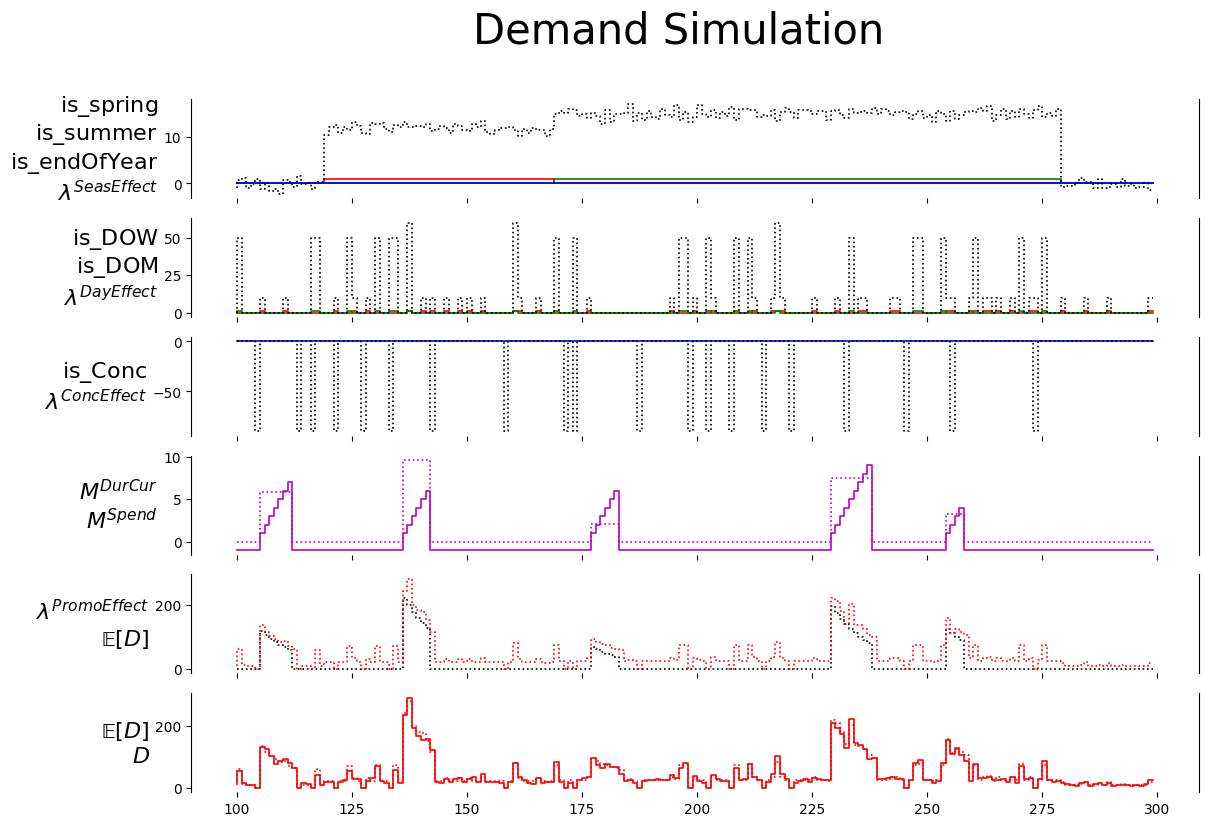

4.6 What Next?

We need some real days from a real calendar, using real holidays. Consider the pandas library for this.
We need to simulate over multiple years.
We need to consider steering the system to optimize an objective, for example, maximize the return on investment in marketing spend.