An RL Approach for Inventory Management (Part 1)

1 Introduction

It is important for an inventory manager to maintain inventory at optimal levels for each kind of product. Too much inventory incurs a holding cost while too little inventory gives rise to a stockout cost. This balancing act could be addressed by framing this problem as a Markov Reward Process. This type of framework is intermediate between a Markov Process (also known as a Markov Chain) and Markov Decision Process. Markov Processes may be presented, in order of increasing complexity, in the following way:

• Markov Process (also called a Markov Chain) which only have states
• Markov Reward Process which adds rewards
• Markov Decision Process which adds actions

In this project we will only investigate the steady-state behavior of the inventory situation. For this we will use a Markov Process, i.e. not a Markov Reward Process. In follow-up projects we will address the aspects of the optimal management of inventory levels.

2 Problem Statement

We need to simulate the steady-state behavior of the inventory situation given the following constraints:

• daily demand for the inventory item comes from a Poisson distribution whose probability mass function (pmf) is given by: \[ f(i) = \frac{e^{-λ}λ^i}{i!} \] where \(\lambda \in \mathbb R_{\ge 0}\) is the Poisson parameter
• the associated cumulative density function (cdf) is given by: \[ F(i) = \sum_{j=0}^if(j) \]
• maximum storage capacity for the inventory item is \(C \in \mathbb Z_{\ge0}\)
• opportunity to order daily at 18h00 when store closes
• ordered items arrive at 06h00 (36 hours later on the day after the day you ordered); i.e. the delivery lead time is 36 hours
• the state of the inventory operation is \((α,β)\) where
  • α is the inventory in the store at 18h00 (on-hand inventory at 18h00)
  • β is the inventory in transit, ordered the previous day; will arrive the next morning at 06h00 (on-order inventory at 18h00)
• ordering policy
  • if \(\alpha+\beta<C\): Order \(C-(\alpha+\beta)\) items
  • if \(\alpha+\beta \ge C\): Order NO items

3 Flow of Events

• Observe the state \(S_t=(α, β)\) at 18h00 (store-closing)
• Immediately order according to the ordering policy
• Receive items at 06h00 (if there was an order 36 hours ago)
• Open the store at 08h00
• Experience random demand according to the demand probability above
  • number of items sold for the day will be the minimum of:
    • demand on the day and
    • inventory at store opening on the day
• Close the store at 18h00 and observe the state \(S_{t+1}\)

4 Steady-State Operation

When this Finite Markov Process runs for a while the constraint \(\alpha+\beta≤C\) becomes satisfied. The finite set of states are \[ \mathcal S = \{(\alpha,\beta)|\alpha \in \mathbb Z_{\ge 0},\beta \in \mathbb Z_{\ge 0},0 \le \alpha + \beta \le C\} \]

When the current state \(S_t = (\alpha, \beta)\): - the order quantity is \(C - (\alpha + \beta)\) - there are only \(\alpha + \beta + 1\) possible next states \[ S_{t+1} = (\alpha + \beta - i, C - (\alpha + \beta)) \] for \(i = 0,1,...,α + β\) - the transition probabilities are \[ \mathcal P((\alpha,\beta), (\alpha+\beta-i, C-(\alpha + \beta))) = f(i)\ \text{for $0 \le i \le \alpha + \beta - 1$} \qquad (4.1) \] \[ \mathcal P((\alpha,\beta), (0, C-(\alpha + \beta))) = \sum_{j=\alpha + \beta}^\infty f(j) = 1 - F(\alpha + \beta - 1) \qquad (4.2) \]

5 Implementation

!python --version

Python 3.7.14

from dataclasses import dataclass
from typing import Mapping, Dict
from scipy.stats import poisson

We make use of the approach followed in http://web.stanford.edu/class/cme241/.

from __future__ import annotations
from abc import ABC, abstractmethod
import random
from typing import Generic, TypeVar, Sequence, Callable, Iterator, Tuple, Iterable, Set
from collections import defaultdict
import graphviz
import numpy as np
from pprint import pprint

5.1 Distributions

Figure 5.1 shows the Python classes used with the inheritance relationships between them.

Figure 5.1 Distribution classes

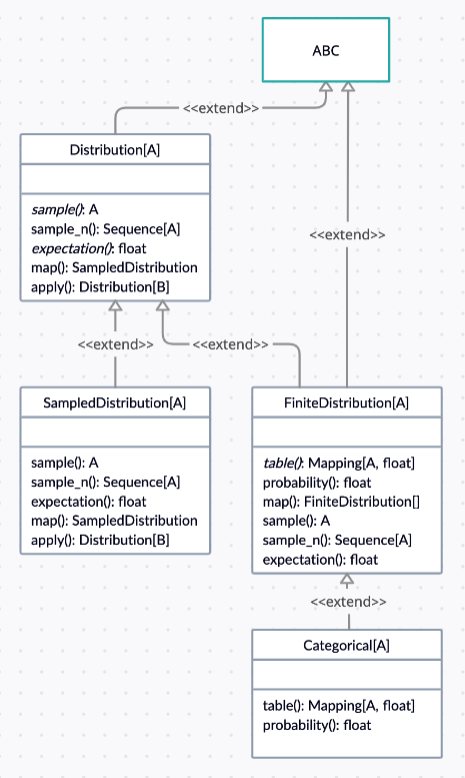
Abstract class Distribution provides a probability distrubtion from which we can sample. The important methods are: - sample - provides a random sample - sample_n - provides n random samples - expectation - finds the expected value of the distribution - map - apply a function to the outcomes of the distribution - apply - apply a function that returns a distribution to the outcomes of the distribution - allows for dependent random variables

A = TypeVar('A')
B = TypeVar('B')
class Distribution(ABC, Generic[A]):
    @abstractmethod
    def sample(self) -> A:
        pass

    def sample_n(self, n: int) -> Sequence[A]: #n random samples
        return [self.sample() for _ in range(n)]

    @abstractmethod
    def expectation(self, f: Callable[[A], float]) -> float:
        pass

    def map(self, f: Callable[[A], B]) -> Distribution[B]:
        return SampledDistribution(lambda: f(self.sample()))

    def apply(self, f: Callable[[A], Distribution[B]]) -> Distribution[B]:
        def sample():
            a = self.sample()
            b_dist = f(a)
            return b_dist.sample()
        return SampledDistribution(sample)

class SampledDistribution allows for a distribution defined by providing a sample function: - sample - provides a random sample - expectation - finds the sampled expectation of f(X) for some f

class SampledDistribution(Distribution[A]):
    sampler: Callable[[], A]
    expectation_samples: int

    def __init__(
        self,
        sampler: Callable[[], A],
        expectation_samples: int = 10000
    ):
        self.sampler = sampler
        self.expectation_samples = expectation_samples

    def sample(self) -> A:
        return self.sampler()

    def expectation( 
        self,
        f: Callable[[A], float]
    ) -> float:
        return 
        sum(f(self.sample()) 
        for _ in range(self.expectation_samples))/self.expectation_samples

class FiniteDistribution provides for a probability distribution with a finite number of outcomes. This allows for rendition of the PDF or CDF in a table. The important methods are: - table - tabular rendition of the PDF - probability - probability of the given outcome - map - return a new distribution that is the result of applying a function to each element of the distribution - sample - provides a random sample - expectation - provides the expectation of the distribution

class FiniteDistribution(Distribution[A], ABC):
    @abstractmethod
    def table(self) -> Mapping[A, float]:
        pass

    def probability(self, outcome: A) -> float:
        return self.table()[outcome]

    def map(self, f: Callable[[A], B]) -> FiniteDistribution[B]:
        result: Dict[B, float] = defaultdict(float)
        for x, p in self:
            result[f(x)] += p
        return Categorical(result)

    def sample(self) -> A:
        outcomes = list(self.table().keys())
        weights = list(self.table().values())
        return random.choices(outcomes, weights=weights)[0]

    def expectation(self, f: Callable[[A], float]) -> float:
        return sum(p * f(x) for x, p in self)

    def __iter__(self) -> Iterator[Tuple[A, float]]:
        return iter(self.table().items())

    def __eq__(self, other: object) -> bool:
        if isinstance(other, FiniteDistribution):
            return self.table() == other.table()
        else:
            return False

    def __repr__(self) -> str:
        return repr(self.table())

class Categorical allow us to select from a finite set of outcomes with the specified probabilities. The important methods are: - table - provides a table of probabilities - probability - provides the probability given an outcome

class Categorical(FiniteDistribution[A]):
    probabilities: Mapping[A, float]

    def __init__(self, distribution: Mapping[A, float]):
        total = sum(distribution.values())
        self.probabilities = {outcome: probability/total #normalized
                              for outcome, probability in distribution.items()}

    def table(self) -> Mapping[A, float]:
        return self.probabilities

    def probability(self, outcome: A) -> float:
        return self.probabilities.get(outcome, 0.)

5.2 Markov Processes

Figure 5.2 shows the Python classes used with the inheritance relationships between them.

Figure 5.2 Markov Process classes

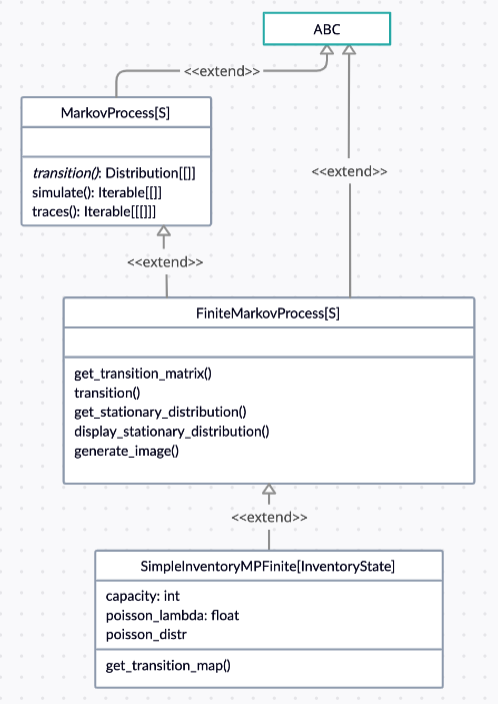
Abstract class State provides the interface for all states:

S = TypeVar('S')
X = TypeVar('X')
class State(ABC, Generic[S]):
    state: S

    def on_non_terminal(
        self,
        f: Callable[[NonTerminal[S]], X],
        default: X
    ) -> X:
        if isinstance(self, NonTerminal):
            return f(self)
        else:
            return default

There are two kinds of states: - Terminal states - Non-Terminal states

@dataclass(frozen=True)
class Terminal(State[S]):
    state: S

@dataclass(frozen=True)
class NonTerminal(State[S]):
    state: S
        
    def __eq__(self, other):
        return self.state == other.state

    def __lt__(self, other):
        return self.state < other.state

class MarkovProcess implements a Markov Process with states of type S. It has methods: - transition - implements the transition propability \[ \begin{aligned} \mathcal P(s,s') &= p(s'|s) \\ &= \mathbb P[S_{t+1}=s'|S_t=s] \end{aligned} \] - given a state of the process, this method returns a distribution of the next states - if the given state is a terminal state, it returns None - simulate - run a simulation trace of this Markov process, generating the states visited during the trace - yields the start state first, then continues yielding subsequent states forever or until we hit a terminal state - traces - yield simulation traces (the output of simulate), sampling a start state from the given distribution each time

class MarkovProcess(ABC, Generic[S]):
    @abstractmethod
    def transition(self, state: NonTerminal[S]) -> Distribution[State[S]]:
        pass

    def simulate(
        self,
        start_state_distribution: Distribution[NonTerminal[S]]
    ) -> Iterable[State[S]]:
        state: State[S] = start_state_distribution.sample()
        yield state
        while isinstance(state, NonTerminal):
            next_distribution = self.transition(state) #.
            #state = self.transition(state).sample() #.
            #state = next_distribution.sample() #.
            next_state = next_distribution.sample() #.
            #yield state #.
            yield next_state #.

    def traces(
        self,
        start_state_distribution: Distribution[NonTerminal[S]]
    ) -> Iterable[Iterable[State[S]]]:
        while True:
            yield self.simulate(start_state_distribution)

A Transition provides a mapping from a NonTermina of S to a FiniteDistribution of State of S:

Transition = Mapping[NonTerminal[S], FiniteDistribution[State[S]]]

class FiniteMarkovProcess provides a Markov Process with a finite state space. This allows the use of tabular methods. Some additional methods are: - get_transition_matrix - provides the transition matrix for the finite Markov Process - get_stationary_distribution - provides the stationary distribution of being in a specific state - generate_image - provides a graphical representation of the state transitions

class FiniteMarkovProcess(MarkovProcess[S]):
    non_terminal_states: Sequence[NonTerminal[S]]
    transition_map: Transition[S]

    def __init__(self, transition_map: Mapping[S, FiniteDistribution[S]]):
        non_terminals: Set[S] = set(transition_map.keys())
        self.transition_map = {
            NonTerminal(s): Categorical(
                {(NonTerminal(s1) if s1 in non_terminals else Terminal(s1)): p
                 for s1, p in v}
            ) for s, v in transition_map.items()
        }
        self.non_terminal_states = list(self.transition_map.keys())

    def __repr__(self) -> str:
        display = ""
        for s, d in self.transition_map.items():
            display += f"From State {s.state}:\n"
            for s1, p in d:
                opt = "Terminal " if isinstance(s1, Terminal) else ""
                display += f"  To {opt}State {s1.state} with Probability {p:.3f}\n"
        return display

    def get_transition_matrix(self) -> np.ndarray:
        sz = len(self.non_terminal_states)
        mat = np.zeros((sz, sz))
        for i, s1 in enumerate(self.non_terminal_states):
            for j, s2 in enumerate(self.non_terminal_states):
                mat[i, j] = self.transition(s1).probability(s2)
        return mat

    def transition(self, state: NonTerminal[S])\
            -> FiniteDistribution[State[S]]:
        return self.transition_map[state]

    def get_stationary_distribution(self) -> FiniteDistribution[S]:
        eig_vals, eig_vecs = np.linalg.eig(self.get_transition_matrix().T)
        index_of_first_unit_eig_val = np.where(
            np.abs(eig_vals - 1) < 1e-8)[0][0]
        eig_vec_of_unit_eig_val = np.real(
            eig_vecs[:, index_of_first_unit_eig_val])
        return Categorical({
            self.non_terminal_states[i].state: ev
            for i, ev in enumerate(eig_vec_of_unit_eig_val /
                                   sum(eig_vec_of_unit_eig_val))
        })

    def display_stationary_distribution(self):
        pprint({
            s: round(p, 3)
            for s, p in self.get_stationary_distribution()
        })

    def generate_image(self) -> graphviz.Digraph:
        d = graphviz.Digraph()
        for s in self.transition_map.keys():
            #d.node(str(s)) #.
            d.node(f"{(s.state.on_hand, s.state.on_order)}") #.
        for s, v in self.transition_map.items():
            for s1, p in v:
                #d.edge(str(s), str(s1), label=str(p)) #.
                #d.edge(str(s), str(s1), label=f'{p:.3f}') #.
                d.edge(f"{(s.state.on_hand, s.state.on_order)}", f"{(s1.state.on_hand, s1.state.on_order)}", label=f'{p:.2f}') #.
        return d        

5.3 Inventory Problem

5.3.1 class InventoryState

Next we will study the operation of the InventoryState class:

# 
# --- study InventoryState

@dataclass(frozen=True)
class InventoryState:
    on_hand: int
    on_order: int

    def inventory_position(self) -> int:
        return self.on_hand + self.on_order

myis = InventoryState(on_hand=3, on_order=4); myis

InventoryState(on_hand=3, on_order=4)

myis.inventory_position()

7

# 
# --- end study InventoryState

5.3.2 class SimpleInventoryMPFinite

Finally, we look at the class SimpleInventoryMPFinite. This provides the implementation of the problem at hand.

class SimpleInventoryMPFinite(FiniteMarkovProcess[InventoryState]):
    def __init__(
        self,
        capacity: int,
        poisson_lambda: float
    ):
        self.capacity: int = capacity
        self.poisson_lambda: float = poisson_lambda
        self.poisson_distr = poisson(poisson_lambda)
        super().__init__(self.get_transition_map())

    def get_transition_map(self) -> \
            Mapping[InventoryState, FiniteDistribution[InventoryState]]:
        d: Dict[InventoryState, Categorical[InventoryState]] = {}
        for alpha in range(self.capacity + 1): #alpha 0 to C
            for beta in range(self.capacity + 1 - alpha): #beta 0 to C - alpha
                state = InventoryState(alpha, beta)
                ip = state.inventory_position()
                beta1 = self.capacity - ip
                state_probs_map: Mapping[InventoryState, float] = {
                    InventoryState(ip - i, beta1):
                    self.poisson_distr.pmf(i) if i < ip else #eq (4.1)
                    1 - self.poisson_distr.cdf(ip - 1) #eq (4.2)
                    for i in range(ip + 1) #i 0 to ip
                }
                d[InventoryState(alpha, beta)] = Categorical(state_probs_map)
        return d

# 
# ---study state_probs_map

capacity = 3
alpha = 2
beta = capacity - alpha; beta 

1

state = InventoryState(alpha, beta); state

InventoryState(on_hand=2, on_order=1)

ip = state.inventory_position(); ip

3

beta1 = capacity - ip; beta1

0

poisson_lambda: float = 1.0
poisson_distr = poisson(poisson_lambda)

{
  InventoryState(ip - i, beta1):
  poisson_distr.pmf(i) if i < ip else
  1 - poisson_distr.cdf(ip - 1)
  for i in range(ip + 1)
}

{InventoryState(on_hand=3, on_order=0): 0.36787944117144233,
 InventoryState(on_hand=2, on_order=0): 0.36787944117144233,
 InventoryState(on_hand=1, on_order=0): 0.18393972058572114,
 InventoryState(on_hand=0, on_order=0): 0.08030139707139416}

# 
# show value of i also
{
  InventoryState(ip - i, beta1):
  [i, poisson_distr.pmf(i)] if i < ip else
  [i, 1 - poisson_distr.cdf(ip - 1)]
  for i in range(ip + 1)
}

{InventoryState(on_hand=3, on_order=0): [0, 0.36787944117144233],
 InventoryState(on_hand=2, on_order=0): [1, 0.36787944117144233],
 InventoryState(on_hand=1, on_order=0): [2, 0.18393972058572114],
 InventoryState(on_hand=0, on_order=0): [3, 0.08030139707139416]}

And now the complete loop:

capacity = 3
for alpha in range(capacity + 1): #alpha 0 to C
    for beta in range(capacity + 1 - alpha): #beta 0 to C - alpha
        state = InventoryState(alpha, beta); print(f'state={state}')
        ip = state.inventory_position(); print(f'ip={ip}')
        beta1 = capacity - ip; print(f'beta1={beta1}')
        state_probs_map: Mapping[InventoryState, float] = {
            InventoryState(ip - i, beta1):
            poisson_distr.pmf(i) if i < ip else #eq (4.1)
            1 - poisson_distr.cdf(ip - 1) #eq (4.2)
            for i in range(ip + 1) #i 0 to ip
        }
state_probs_map

state=InventoryState(on_hand=0, on_order=0)
ip=0
beta1=3
state=InventoryState(on_hand=0, on_order=1)
ip=1
beta1=2
state=InventoryState(on_hand=0, on_order=2)
ip=2
beta1=1
state=InventoryState(on_hand=0, on_order=3)
ip=3
beta1=0
state=InventoryState(on_hand=1, on_order=0)
ip=1
beta1=2
state=InventoryState(on_hand=1, on_order=1)
ip=2
beta1=1
state=InventoryState(on_hand=1, on_order=2)
ip=3
beta1=0
state=InventoryState(on_hand=2, on_order=0)
ip=2
beta1=1
state=InventoryState(on_hand=2, on_order=1)
ip=3
beta1=0
state=InventoryState(on_hand=3, on_order=0)
ip=3
beta1=0

{InventoryState(on_hand=3, on_order=0): 0.36787944117144233,
 InventoryState(on_hand=2, on_order=0): 0.36787944117144233,
 InventoryState(on_hand=1, on_order=0): 0.18393972058572114,
 InventoryState(on_hand=0, on_order=0): 0.08030139707139416}

# 
# ---end study state_probs_map

5.3.3 Experiment

Next, we create an instance of the class SimpleInventoryMPFinite with: - item_capacity = 3 - item_poisson_lambda = 1.0

item_capacity = 3
item_poisson_lambda = 1.0
si_mp = SimpleInventoryMPFinite(
    capacity=item_capacity,
    poisson_lambda=item_poisson_lambda
)

6 Visualization

6.1 State Transitions

Here is the transition map:

print("Transition Map")
print("--------------")
si_mp

Transition Map
--------------

From State InventoryState(on_hand=0, on_order=0):
  To State InventoryState(on_hand=0, on_order=3) with Probability 1.000
From State InventoryState(on_hand=0, on_order=1):
  To State InventoryState(on_hand=1, on_order=2) with Probability 0.368
  To State InventoryState(on_hand=0, on_order=2) with Probability 0.632
From State InventoryState(on_hand=0, on_order=2):
  To State InventoryState(on_hand=2, on_order=1) with Probability 0.368
  To State InventoryState(on_hand=1, on_order=1) with Probability 0.368
  To State InventoryState(on_hand=0, on_order=1) with Probability 0.264
From State InventoryState(on_hand=0, on_order=3):
  To State InventoryState(on_hand=3, on_order=0) with Probability 0.368
  To State InventoryState(on_hand=2, on_order=0) with Probability 0.368
  To State InventoryState(on_hand=1, on_order=0) with Probability 0.184
  To State InventoryState(on_hand=0, on_order=0) with Probability 0.080
From State InventoryState(on_hand=1, on_order=0):
  To State InventoryState(on_hand=1, on_order=2) with Probability 0.368
  To State InventoryState(on_hand=0, on_order=2) with Probability 0.632
From State InventoryState(on_hand=1, on_order=1):
  To State InventoryState(on_hand=2, on_order=1) with Probability 0.368
  To State InventoryState(on_hand=1, on_order=1) with Probability 0.368
  To State InventoryState(on_hand=0, on_order=1) with Probability 0.264
From State InventoryState(on_hand=1, on_order=2):
  To State InventoryState(on_hand=3, on_order=0) with Probability 0.368
  To State InventoryState(on_hand=2, on_order=0) with Probability 0.368
  To State InventoryState(on_hand=1, on_order=0) with Probability 0.184
  To State InventoryState(on_hand=0, on_order=0) with Probability 0.080
From State InventoryState(on_hand=2, on_order=0):
  To State InventoryState(on_hand=2, on_order=1) with Probability 0.368
  To State InventoryState(on_hand=1, on_order=1) with Probability 0.368
  To State InventoryState(on_hand=0, on_order=1) with Probability 0.264
From State InventoryState(on_hand=2, on_order=1):
  To State InventoryState(on_hand=3, on_order=0) with Probability 0.368
  To State InventoryState(on_hand=2, on_order=0) with Probability 0.368
  To State InventoryState(on_hand=1, on_order=0) with Probability 0.184
  To State InventoryState(on_hand=0, on_order=0) with Probability 0.080
From State InventoryState(on_hand=3, on_order=0):
  To State InventoryState(on_hand=3, on_order=0) with Probability 0.368
  To State InventoryState(on_hand=2, on_order=0) with Probability 0.368
  To State InventoryState(on_hand=1, on_order=0) with Probability 0.184
  To State InventoryState(on_hand=0, on_order=0) with Probability 0.080

The following diagram shows the states for the case when the capacity is 3. The transition probabilties are also shown.

si_mp.generate_image()

6.2 Stationary Distributions of States

Here is the stationary distribution of states:

print("Stationary Distribution")
print("-----------------------")
si_mp.display_stationary_distribution()
print()

Stationary Distribution
-----------------------
{InventoryState(on_hand=2, on_order=0): 0.143,
 InventoryState(on_hand=2, on_order=1): 0.148,
 InventoryState(on_hand=0, on_order=1): 0.107,
 InventoryState(on_hand=0, on_order=0): 0.031,
 InventoryState(on_hand=3, on_order=0): 0.143,
 InventoryState(on_hand=1, on_order=2): 0.065,
 InventoryState(on_hand=1, on_order=0): 0.071,
 InventoryState(on_hand=0, on_order=3): 0.031,
 InventoryState(on_hand=1, on_order=1): 0.148,
 InventoryState(on_hand=0, on_order=2): 0.112}

from mpl_toolkits.mplot3d import axes3d
import matplotlib.pyplot as plt
import numpy as np
from matplotlib import style
# style.use('ggplot')
import matplotlib.ticker as ticker

fig = plt.figure(figsize=(15, 10))
ax1 = fig.add_subplot(111, projection='3d')

list_of_tuples = [(el[0].on_hand, el[0].on_order, el[1]) for el in si_mp.get_stationary_distribution()]; #list_of_tuples
x3, y3, dz = [list(tup) for tup in zip(*list_of_tuples)]; x3, y3, dz

# x3 = [0, 1, 2, 1, 0, 0]
# y3 = [0, 1, 0, 0, 2, 1]
n = len(dz)
z3 = np.zeros(n)
dx = np.ones(n)
dy = np.ones(n)
# dz = [0.117, 0.162, 0.162, 0.162, 0.117, 0.279]

ax1.bar3d(x3, y3, z3, dx, dy, dz)

ax1.set_xticks([e+0.5 for e in range(n - 1)])
ax1.set_xticklabels(range(n - 1))
ax1.set_xlabel(r'on-hand inventory, $\alpha$', fontsize=15)

ax1.set_yticks([e+0.5 for e in range(n - 1)])
ax1.set_yticklabels(range(n - 1))
ax1.set_ylabel(r'on-order inventory, $\beta$', fontsize=15)

ax1.set_zlabel(r'probability, $\pi$', fontsize=15)
ax1.set_title('Stationary Distribution of States', fontsize=20)
ax1.view_init(ax1.elev + 20, -200)
plt.show()

6.3 Traces

Next we visualize how each of the state variables, \(\alpha\) and \(\beta\), evolve over time.

# 
# use stationary distribution for a start state distribution
ssd = si_mp.get_stationary_distribution(); ssd

{InventoryState(on_hand=0, on_order=0): 0.031120936942690133, InventoryState(on_hand=0, on_order=1): 0.10660457196659985, InventoryState(on_hand=0, on_order=2): 0.11244837477707609, InventoryState(on_hand=0, on_order=3): 0.03112093694269009, InventoryState(on_hand=1, on_order=0): 0.07128613765604674, InventoryState(on_hand=1, on_order=1): 0.1484160781225697, InventoryState(on_hand=1, on_order=2): 0.0654423348455706, InventoryState(on_hand=2, on_order=0): 0.14257227531209354, InventoryState(on_hand=2, on_order=1): 0.1484160781225697, InventoryState(on_hand=3, on_order=0): 0.14257227531209354}

# 
# create a generator for the states of a trace
gen = si_mp.traces(start_state_distribution=ssd); gen

<generator object MarkovProcess.traces at 0x7ff8924922d0>

# 
# get a trace
a_trace = [list(next(gen)) for i in range(50)]; a_trace

[[InventoryState(on_hand=2, on_order=0)],
 [InventoryState(on_hand=2, on_order=1)],
 [InventoryState(on_hand=0, on_order=2)],
 [InventoryState(on_hand=1, on_order=1)],
 [InventoryState(on_hand=0, on_order=1)],
 [InventoryState(on_hand=0, on_order=3)],
 [InventoryState(on_hand=0, on_order=2)],
 [InventoryState(on_hand=1, on_order=1)],
 [InventoryState(on_hand=1, on_order=1)],
 [InventoryState(on_hand=1, on_order=1)],
 [InventoryState(on_hand=1, on_order=1)],
 [InventoryState(on_hand=1, on_order=2)],
 [InventoryState(on_hand=2, on_order=1)],
 [InventoryState(on_hand=1, on_order=0)],
 [InventoryState(on_hand=0, on_order=0)],
 [InventoryState(on_hand=1, on_order=1)],
 [InventoryState(on_hand=2, on_order=1)],
 [InventoryState(on_hand=1, on_order=0)],
 [InventoryState(on_hand=1, on_order=0)],
 [InventoryState(on_hand=0, on_order=1)],
 [InventoryState(on_hand=0, on_order=1)],
 [InventoryState(on_hand=2, on_order=1)],
 [InventoryState(on_hand=2, on_order=0)],
 [InventoryState(on_hand=3, on_order=0)],
 [InventoryState(on_hand=2, on_order=1)],
 [InventoryState(on_hand=2, on_order=1)],
 [InventoryState(on_hand=1, on_order=1)],
 [InventoryState(on_hand=2, on_order=1)],
 [InventoryState(on_hand=1, on_order=1)],
 [InventoryState(on_hand=0, on_order=1)],
 [InventoryState(on_hand=1, on_order=1)],
 [InventoryState(on_hand=1, on_order=1)],
 [InventoryState(on_hand=0, on_order=2)],
 [InventoryState(on_hand=1, on_order=1)],
 [InventoryState(on_hand=1, on_order=0)],
 [InventoryState(on_hand=2, on_order=0)],
 [InventoryState(on_hand=2, on_order=1)],
 [InventoryState(on_hand=1, on_order=1)],
 [InventoryState(on_hand=2, on_order=1)],
 [InventoryState(on_hand=0, on_order=3)],
 [InventoryState(on_hand=2, on_order=0)],
 [InventoryState(on_hand=1, on_order=1)],
 [InventoryState(on_hand=3, on_order=0)],
 [InventoryState(on_hand=2, on_order=1)],
 [InventoryState(on_hand=0, on_order=1)],
 [InventoryState(on_hand=1, on_order=1)],
 [InventoryState(on_hand=0, on_order=2)],
 [InventoryState(on_hand=0, on_order=0)],
 [InventoryState(on_hand=3, on_order=0)],
 [InventoryState(on_hand=2, on_order=1)]]

# 
# get a list of numeric tuples from the trace
list_of_tuples = [(state[0].on_hand, state[0].on_order) for state in a_trace]; list_of_tuples

[(2, 0),
 (2, 1),
 (0, 2),
 (1, 1),
 (0, 1),
 (0, 3),
 (0, 2),
 (1, 1),
 (1, 1),
 (1, 1),
 (1, 1),
 (1, 2),
 (2, 1),
 (1, 0),
 (0, 0),
 (1, 1),
 (2, 1),
 (1, 0),
 (1, 0),
 (0, 1),
 (0, 1),
 (2, 1),
 (2, 0),
 (3, 0),
 (2, 1),
 (2, 1),
 (1, 1),
 (2, 1),
 (1, 1),
 (0, 1),
 (1, 1),
 (1, 1),
 (0, 2),
 (1, 1),
 (1, 0),
 (2, 0),
 (2, 1),
 (1, 1),
 (2, 1),
 (0, 3),
 (2, 0),
 (1, 1),
 (3, 0),
 (2, 1),
 (0, 1),
 (1, 1),
 (0, 2),
 (0, 0),
 (3, 0),
 (2, 1)]

# 
# collect each state variable's values in a list
alpha, beta = [list(tup) for tup in zip(*list_of_tuples)]; #alpha, beta

n_steps = len(alpha); n_steps #number of steps

50

figure, axis = plt.subplots(2, 1)
figure.set_figwidth(15)
figure.set_figheight(8)

axis[0].step(range(n_steps), alpha)
axis[0].set_ylim([0, 4])
axis[0].set_title(r"state variable $\alpha$")

axis[1].step(range(n_steps), beta)
axis[1].set_ylim([0, 4])
axis[1].set_title(r"state variable $\beta$");